
高校数学をプログラミングで解く(数学B編)「4-6 二項分布」
はじめに
今回は、数学Bで学ぶ「二項分布」について、二項分布を関数化し、その関数を用いて、確率や平均、分散、標準偏差を計算するプログラムを作成します。
二項分布
まず、二項分布について解説しておきます。
二項分布 $${B(n,p)}$$
$$
P(X=r) = {}_nC_r p^r q^{n-r} \ \ (0 < p < 1, q = 1-p)
$$
で与えられる確率分布。ただし、$${r=0,1,2,\cdots, n}$$。
平均、分散、標準偏差
確率変数$${X}$$が二項分布$${B(n,p)}$$に従うとき、
$$
E(X) = np, \ \ V(X)=npq, \ \ \sigma(X) = \sqrt{npq} \ \ (q=1-p)
$$
なお、この二項分布は、記事『高校数学をプログラミングで解く(数学A編)「1-7 反復試行の確率」』で紹介した「反復試行の確率」と同じものになっています。
二項分布の関数化
二項分布を関数として準備しておきます。
二項分布は、異なる$${n}$$個のものから$${r}$$個を取る組合せの総数$${{}_nC_r}$$と、べき乗$${p^r, q^{n-r}}$$の積で表されます。$${{}_nC_r}$$については、記事『高校数学をプログラミングで解く(数学A編)「1-7 反復試行の確率」』で関数として準備したので、それを再利用します。
// 異なるn個のものからr個を取る組合せの総数
int combination(int n, int r){
int p = 1; // 組合せの総数の分子
int q = 1; // 組合せの総数の分母
for(int i=0; i<r; i++){
p = p * (n-i);
q = q * (r-i);
}
int c = p / q; // 組合せの総数を計算
return c; // 組合せの総数を出力
}ソースコード1 異なる$${n}$$個のものから$${r}$$個を取る組合せの総数$${{}_nC_r}$$
べき乗$${p^r, q^{n-r}}$$については、こちらも記事『高校数学をプログラミングで解く(数学A編)「1-7 反復試行の確率」』で紹介しているように pow 関数を利用します。これらを利用すると、二項分布の関数 binomialdistribution を以下のように作成することができます。
// 二項分布の関数
float binomialdistribution(
int n, // 試行回数
float p, // 成功確率
int r // 確率変数の値
){
float P = combination(n,r) * pow(p, r) * pow(1.0-p, n-r);
return P;
}ソースコード2 二項分布の関数
なお、二項分布の関数 binomialdistribution の引数は、
n:試行回数 int型
p:成功確率 float型
r:確率変数の値 int型
とし、返り値は二項分布から計算された確率の値(float型)となっています。
二項分布による確率を計算する
今回は次のような問題を考えてみます。
問題1
1個のさいころを10回投げるとき、偶数の目が出た回数を$${X}$$とする。$${X}$$はどのような二項分布に従うか。また、次の確率を求めよ。
(1) $${P(X=2)}$$
(2) $${P(5 \leq X \leq 7)}$$
(3) $${P(X \leq 8)}$$
なお、今回、「どのような二項分布に従うか」の部分が$${B(10, 1/2)}$$であることはわかっているとして、3つの確率の計算を行うプログラムを作成していきます。
アルゴリズム設計
確率の計算自体は簡単です。偶数の目が出る確率は$${p=1/2}$$であることを考慮して、3つの確率はそれぞれ
$$
P(X=2) = {}_{10}C_2 p^2 q^8
$$
$$
P(5 \leq X \leq 7) = {}_{10}C_5 p^5 q^5 + {}_{10}C_6 p^6 q^4 + {}_{10}C_7 p^7 q^3
$$
$$
P(X \leq 8) = \sum_{r=0}^8 {}_{10}C_r p^r q^{10-r}
$$
で計算することができます。なお、$${P(X \leq 8)}$$については、本来
$$
P(X \leq 8) = 1-\sum_{r=9}^{10} {}_{10}C_r p^r q^{10-r}
$$
で計算するべきですが、今回は二項分布の確率の9個の和で計算しています。
プログラム
では、問題1の3つの二項分布による確率を計算するプログラムを作成していきます。
// 1個のさいころを10回投げるとき、
// 偶数の目が出た回数の確率
void setup(){
int n = 10; // さいころを投げる回数
float p = 1.0/2.0; // 偶数の目が出る確率
// (1) P(X=2)
float p1 = binomialdistribution(n, p, 2);
// (2) P(5≦X≦7)
float p2 = 0.0;
for(int r=5; r<=7; r++){
p2 = p2 + binomialdistribution(n, p, r);
}
// (3) P(X≦8)
float p3 = 0.0;
for(int r=0; r<=8; r++){
p3 = p3 + binomialdistribution(n, p, r);
}
// それぞれの確率の値をコンソールに出力
println("P(X=2) =", p1);
println("P(5≦X≦7)=", p2);
println("P(X≦8) =", p3);
}
// 二項分布の関数
float binomialdistribution(
int n, // 試行回数
float p, // 成功確率
int r // 確率変数の値
){
float P = combination(n,r) * pow(p, r) * pow(1.0-p, n-r);
return P;
}
// 異なるn個のものからr個を取る組合せの総数
int combination(int n, int r){
int p = 1; // 組合せの総数の分子
int q = 1; // 組合せの総数の分母
for(int i=0; i<r; i++){
p = p * (n-i);
q = q * (r-i);
}
int c = p / q; // 組合せの総数を計算
return c; // 組合せの総数を返す
}ソースコード3 二項分布による計算するプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「Probability_BinomialDistribution」としています)、テキストエディタ部分に書いて実行します。
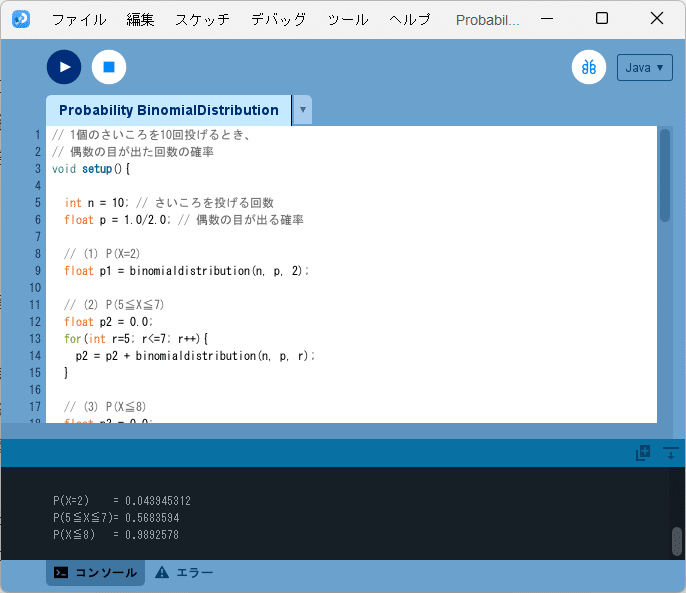
図1のように、3つの二項分布による確率が、
P(X=2) = 0.043945312
P(5≦X≦7)= 0.5683594
P(X≦8) = 0.9892578
とコンソールに出力されます。なお、これらの値を分数で表すと、それぞれ順に
$$
\frac{45}{1024}, \ \ \frac{291}{512}, \ \ \frac{1013}{1024}
$$
となります。
二項分布による平均、分散、標準偏差を計算する
二項分布による平均、分散、標準偏差を計算するにあたり、今回は次のような問題を考えてみます。
問題2
次の二項分布の平均、分散と標準偏差を求めよ。
(1) $${B(8,1/2)}$$
(2) $${B(5,1/4)}$$
(3) $${B(12,2/3)}$$
アルゴリズム設計
この問題は二項分布の平均、分散と標準偏差の公式を利用すれば、簡単に計算することができますが、今回は敢えて二項分布の平均、分散と標準偏差の定義を用いて計算し、公式の結果と比較するようにします。なお、二項分布の平均$${m}$$と分散$${v}$$の定義を用いた計算式はそれぞれ
$$
m= \sum_{r=0}^n r {}_{n}C_r p^r q^{n-r}
$$
と
$$
v= \sum_{r=0}^n (r-m)^2 {}_{n}C_r p^r q^{n-r}
$$
で表されます。
プログラム
では、二項分布による平均、分散、標準偏差を計算するプログラムを作成していきます。なお、このプログラムは問題2(1)の結果を出力するものになっています。
// 二項分布の平均、分散と標準偏差を計算する
void setup(){
int n = 8; // 試行回数
float p = 1.0/2.0; // 成功確率
float m = 0.0; // 平均
for(int r=0; r<=n; r++){
m = m + r * binomialdistribution(n, p, r);
}
float v = 0.0; // 分散
for(int r=0; r<=n; r++){
v = v + (r-m) * (r-m) * binomialdistribution(n, p, r);
}
// 標準偏差
float sigma = sqrt(v);
// 定義による計算結果と公式による計算結果ををコンソールに出力
println("定義による計算結果 平均:",m, "分散:", v, "標準偏差:", sigma);
println("公式による計算結果 平均:",n*p, "分散:", n*p*(1.0-p), "標準偏差:", sqrt(n*p*(1.0-p)));
}
// 二項分布の関数
float binomialdistribution(
int n, // 試行回数
float p, // 成功確率
int r // 確率変数の値
){
float P = combination(n,r) * pow(p, r) * pow(1.0-p, n-r);
return P;
}
// 異なるn個のものからr個を取る組合せの総数
int combination(int n, int r){
int p = 1; // 組合せの総数の分子
int q = 1; // 組合せの総数の分母
for(int i=0; i<r; i++){
p = p * (n-i);
q = q * (r-i);
}
int c = p / q; // 組合せの総数を計算
return c; // 組合せの総数を返す
}ソースコード4 二項分布による平均、分散、標準偏差を計算するプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「MeanandVariance_BinomialDistribution」としています)、テキストエディタ部分に書いて実行します。

図2のように、問題2(1)の二項分布による平均、分散、標準偏差が、定義を用いた場合と公式を用いた場合とで
定義による計算結果 平均: 4.0 分散: 2.0 標準偏差: 1.4142135
公式による計算結果 平均: 4.0 分散: 2.0 標準偏差: 1.4142135
とコンソールに出力されます。
また、問題2の(2)と(3)についても、二項分布による平均、分散、標準偏差を計算するプログラム(ソースコード4)の中の変数 n と p とを問題に合わせて調整することで結果を得ることができます。結果として、問題2(2)は、
定義による計算結果 平均: 1.25 分散: 0.9375 標準偏差: 0.96824586
公式による計算結果 平均: 1.25 分散: 0.9375 標準偏差: 0.96824586
と出力され、問題2(3)は、
定義による計算結果 平均: 8.000001 分散: 2.6666665 標準偏差: 1.6329931
公式による計算結果 平均: 8.0 分散: 2.6666665 標準偏差: 1.6329931
と出力されるはずですので、試してみてください。
まとめ
今回は、数学Bで学ぶ「二項分布」について、二項分布を関数化し、その関数を用いて、確率や平均、分散、標準偏差を計算するプログラムを作成しました。
二項分布は、記事『高校数学をプログラミングで解く(数学A編)「1-7 反復試行の確率」』で紹介した「反復試行の確率」と同じものになっていますので、そのとき作成した$${{}_nC_r}$$の関数を再利用して、二項分布を関数化しました。そして、この二項分布の関数 binomialdistribution を用いて、二項分布による確率を計算するプログラムや二項分布による平均、分散、標準偏差を計算するプログラムを作成しました。
二項分布による平均、分散、標準偏差を計算するプログラムでは、二項分布による平均、分散を定義通りに計算する方法と公式を用いて計算する方法と2通りで計算して結果を比較しました。このように、計算結果や公式が正しいかどうかを確かめるためにプログラムを書くということも有効な場合がありますので、そのような使い方もあることを覚えておいてください。なお、二項分布による平均、分散の公式の証明は和のルールを調整することで比較的簡単にできますので、一度チャレンジしてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
この記事が気に入ったらサポートをしてみませんか?
