
エラトステネスの篩(ふるい)で100までにある素数を見つける方法
素数を見つける方法の1つであるエラトステネスの篩(ふるい)をご紹介します!
エラトステネスの篩とは?
エラトステネスの篩とは素数は「約数が2つしかない(1と自分自身の2つ)」という性質を利用して素数を見つける方法です。まずは動画をご紹介。動画の下部に、文章で説明もしてあります。
最初に1を消します。次に、2は素数ですので「〇」を書きます。ですがその倍数は約数に必ず2が入ってしまうので素数ではありません。
なので2より大きい2の倍数を消していきます。

写真をみてみると消されていないマスの数はどれも2の倍数でではないですよね。消されずに残っているマスのうち一番小さい数はは3になりました。同様に3の倍数も消してみると

だんだん残っている数が少なくなってきましたね。また同じ様に一番小さい何も書いていないマスは5になので同様に5の倍数も消してみます。

何も書いていない数を見ると九九表ではみない数が多くなってきました。
次に7の倍数を消していきます。
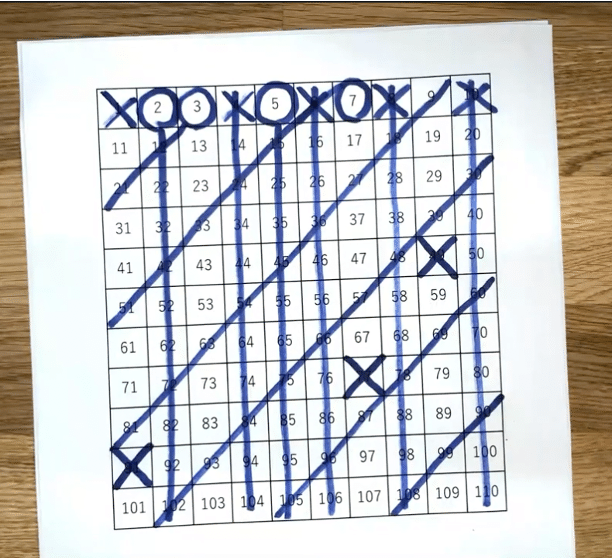
7までくると新たに消すところは3か所とだいぶ少なくなりましたね。
実は7まで調べるとこの方法では120までの素数を探し出すことができます。
(11まで調べると168まで素数を探し出すことができます)
後書きになぜかを簡単に説明します。
エラトステネスの篩、いかがでしたでしょうか?
また、やってみたいという方はぜひ写真で使っているシートをダウンロードして試してみてください!
あとがき
なぜ素数を探し出せるのかを36を例として簡単に説明していきます。
36の約数は1,2,3,4,6,9,12,18,36の9個です。これを以下の様にしてみます。
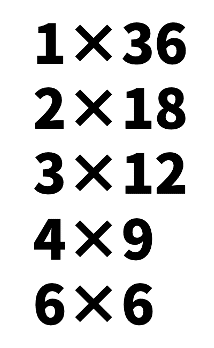
上の式はどの数も答えは36になっていますよね。
この様に約数は元の数を割り切れる数なので約数にある数をかけると元の数に戻ります。
なので
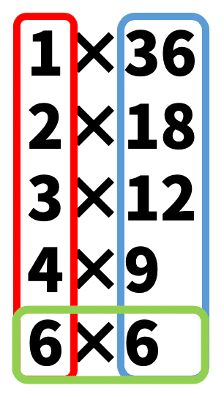
赤い線で囲まれた数字を見つけることができればその数を使って青い線で囲まれた数を見つけることができます。なので、緑色の数字の折り返し地点まで調べれば全ての約数を見つけることができます。
緑色の数は元の数の平方根になっています。数学では√を使って表されます。今回は元の数が36なので√36の正の値である6までの数を調べると全ての約数がもとまります。
37で試す場合も√37はすぐには分かりませんが、平方根の整数部分が7になるのは7×7=49で49以上なので、36≦37<49である37の平方根の値の整数部分は6とわかります。なので37を1〜6までの数で割っていくと全ての約数を求めることができ、もし1でしか割れなかったら37は素数であるとわかります。
今回の表は110まで書いてありますが110の平方根の整数部分は10になります。(10×10=100、11×11=121なので)
10以下の素数は2,3,5,7の4つでこれら全ての倍数を消しているので残っている数は全て素数になります。
この記事が気に入ったらサポートをしてみませんか?
