
2020年東京大学理系第2問
こんにちは。しろ@です。
自分が受験した年の受験校の問題を全部取り上げるシリーズ第1弾(東大)、今回は2020年東京大学理系第2問を取り上げます!
問題
問題は以下の通りです。
平面上の点$${\mathrm{P, Q, R}}$$が同一直線上にないとき、それらを3頂点とする三角形の面積を$${\triangle\mathrm{PQR}}$$で表す。また、$${\mathrm{P, Q, R}}$$が同一直線上にあるときは、$${\triangle\mathrm{PQR}=0}$$とする。
$${\mathrm{A, B, C}}$$を平面上の3点とし、$${\triangle\mathrm{ABC}=1}$$とする。この平面上の点$${\mathrm{X}}$$が
$$
2\leqq\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}\leqq3
$$
を満たしながら動くとき、$${\mathrm{X}}$$の動きうる範囲の面積を求めよ。
問題集にあるような典型問題ではなさそうなのでとっつきにくさを感じます。とりあえず適当に図を描いてみてどうなるか考えてみましょう。
考え方
手始めに、$${\mathrm{X}}$$を$${\triangle\mathrm{ABC}}$$の周または内部にとってみると、$${\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=1}$$になってしまうので不適です。
というわけで、$${\mathrm{X}}$$を$${\triangle\mathrm{ABC}}$$の外部にとることだけを考えます!たとえば、次のような図1だったらどうなるでしょうか。

図1のとき、$${\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=赤+青+緑=2\times赤+\triangle\mathrm{ABC}=2\times赤+1}$$となります。
では、次のような図2ならどうでしょうか。
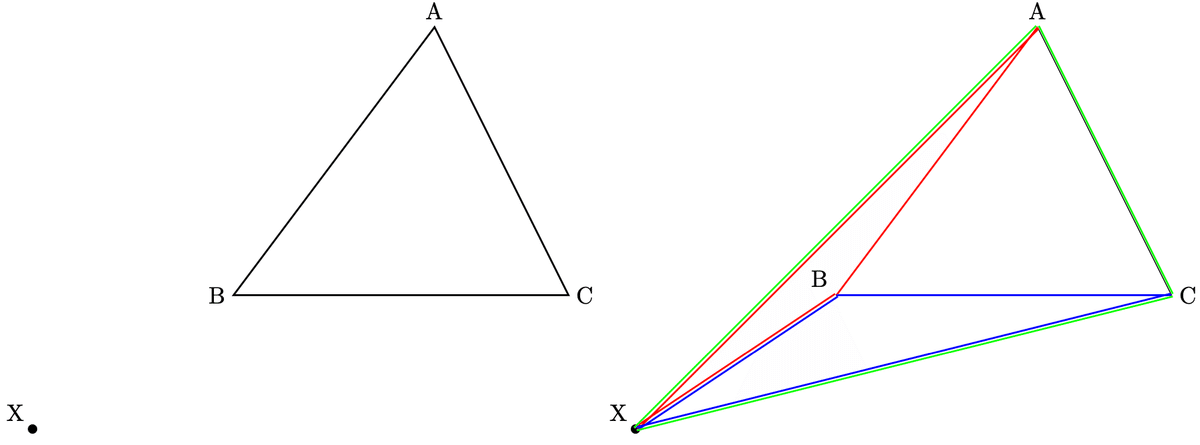
図2のとき、$${\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=赤+青+緑=2\times緑-\triangle\mathrm{ABC}=2\times緑-1}$$となります。
$${\mathrm{X}}$$の位置の分類としてはこの2種類があることが分かるでしょう。もう少し正確に分類するなら、次の図3における①〜⑥のように分類できます。

あとは不等式と照らし合わせて、$${\mathrm{X}}$$がどの位置に来るのか議論すればよさそうです。$${\mathrm{X}}$$が動く範囲だけ求めて、面積の計算を忘れるということがないように!(誰かさんが受験生のとき忘れかけた記憶。)
解答
今回は受験生時代と同じく、縦に分割して解答を書いてみました!いくつか図を描くので分割しないとスペースがもったいないというのもありましたが…逆に1行で書く数式が長い場合などは分割しない方がいいかもしれませんね。

解説
まず、図1と図2の各場合に$${\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=赤+青+緑}$$がどのようになるか求めます。$${赤+青+緑}$$のままだと、$${\mathrm{X}}$$を動かしたときに赤、青、緑が全部動いてしまうので、不等式が成り立つような$${\mathrm{X}}$$の条件を考えづらいです。
そこで、$${赤+青+緑}$$を赤、青、緑のいずれか1つだけで表し、$${\mathrm{X}}$$に合わせて動く文字を1つにできないかと考えます。(イメージとしては、$${x}$$と$${y}$$をつなぐ式を用いて、2変数関数$${f(x, y)}$$を1文字消去して1変数関数$${f(x)}$$or$${f(y)}$$にするのと同じ)
図1の場合は$${2\times赤+1}$$、図2の場合は$${2\times緑-1}$$と書けることが分かります!これらが$${2}$$以上$${3}$$以下になるような条件を求めます。
まず、図1の場合は$${\displaystyle\frac{1}{2}\leqq赤\leqq1}$$となります。$${\triangle\mathrm{ABC}=1}$$ですので、$${\mathrm{AB}}$$を底辺とみて高さを$${\mathrm{X}}$$で調整すればよいですね。
次に、図2の場合は$${\displaystyle\frac{3}{2}\leqq緑\leqq2}$$となります。$${\triangle\mathrm{ABC}=1}$$ですので、$${\mathrm{CA}}$$を底辺とみて高さを$${\mathrm{X}}$$で調整すればよいですね。
あとは面積を求めるだけです!$${\triangle{\mathrm{ABC}}}$$と相似な図形が出てくるので、相似比を使って頑張って求めましょう。
最後にコメント
個人的な難易度は「やや易〜標準」です。時間があれば完答できる人も多いと思いますが、典型問題ではなくその場で考える思考力が必要になるので、初動のとっつきにくさがあります。第1問もそういう性質がありましたね。本問も制限時間内でキレイな解答を仕上げる難しさがあると思います。
また、ベクトルを使った解法や座標に乗っける解法もあるようですが、個人的にはあくまで別解という感じがします。少なくとも自分は初動でベクトルや座標を持ち出すことはない気がします。
自分が受験したときは、$${\mathrm{X}}$$が動く範囲だけ求めて満足して、第3問に進んだ記憶があります。見直しのときに、「これ面積求めるやつじゃん!」と気づき、終了直前でわちゃわちゃ計算した気がします。(たしか間違えた。)
というわけで今回の記事はここまで。
最後までお読みいただきありがとうございました。もしよろしければ、次回以降の記事もお読みいただけると嬉しいです。
それでは、また次の記事で。
2024.02.19
しろ@
この記事が気に入ったらサポートをしてみませんか?
