
2020年東京大学理系第4問
こんにちは。しろ@です。
自分が受験した年の受験校の問題を全部取り上げるシリーズ第1弾(東大)、今回は2020年東京大学理系第4問です!
問題
問題は次の通りです。
$${n, k}$$を、$${1\leqq k\leqq n}$$を満たす整数とする。$${n}$$個の整数
$$
2^m\quad(m=0, 1, 2, \dots, n-1)
$$
から異なる$${k}$$個を選んでそれらの積をとる。$${k}$$個の整数の選び方すべてに対しこのように積をとることにより得られる$${{}_n\mathrm{C}_k}$$個の整数の和を$${a_{n, k}}$$とおく。例えば、
$$
a_{4, 3}=2^0\cdot2^1\cdot2^2+2^0\cdot2^1\cdot2^3+2^0\cdot2^2\cdot2^3+2^1\cdot2^2\cdot2^3=120
$$
である。
(1) $${2}$$以上の整数$${n}$$に対し、$${a_{n, 2}}$$を求めよ。
(2) $${1}$$以上の整数$${n}$$に対し、$${x}$$についての等式
$$
f_n(x)=1+a_{n, 1}x+a_{n, 2}x^2+\dots+a_{n, n}x^n
$$
を考える。$${\displaystyle\frac{f_{n+1}(x)}{f_n(x)}}$$と$${\displaystyle\frac{f_{n+1}(x)}{f_{n}(2x)}}$$を$${x}$$についての整式として表せ。
(3) $${\displaystyle\frac{a_{n+1, k+1}}{a_{n, k}}}$$を$${n, k}$$で表せ。
パッと見で何を言ってるか分からない!最初から読み解いていきましょう。いま、$${n}$$個の整数
$$
2^0, 2^1, 2^2, \dots, 2^{n-1}
$$
があります。この$${n}$$個から$${k}$$個を選んでその積をとります。$${k}$$個の選び方は$${{}_n\mathrm{C}_k}$$通りあるわけですが、その$${{}_n\mathrm{C}_k}$$通りの積をすべて足したものを$${a_{n, k}}$$とするのです。
試しに$${n=4}$$の場合を列挙してみると、
$$
\begin{array}{}
a_{4, 1}&=&2^0+2^1+2^2+2^3\\
a_{4, 2}&=&2^0\cdot2^1+2^0\cdot2^2+2^0\cdot2^3+2^1\cdot2^2+2^1\cdot2^3+2^2\cdot2^3\\
a_{4, 3}&=&2^0\cdot2^1\cdot2^2+2^0\cdot2^1\cdot2^3+2^0\cdot2^2\cdot2^3+2^1\cdot2^2\cdot2^3\\
a_{4, 4}&=&2^0\cdot2^1\cdot2^2\cdot2^3
\end{array}
$$
となります。うーんまぁ計算方法は分かったけど…という感じですが、とりあえず(1)から解いていきましょうか。
解答

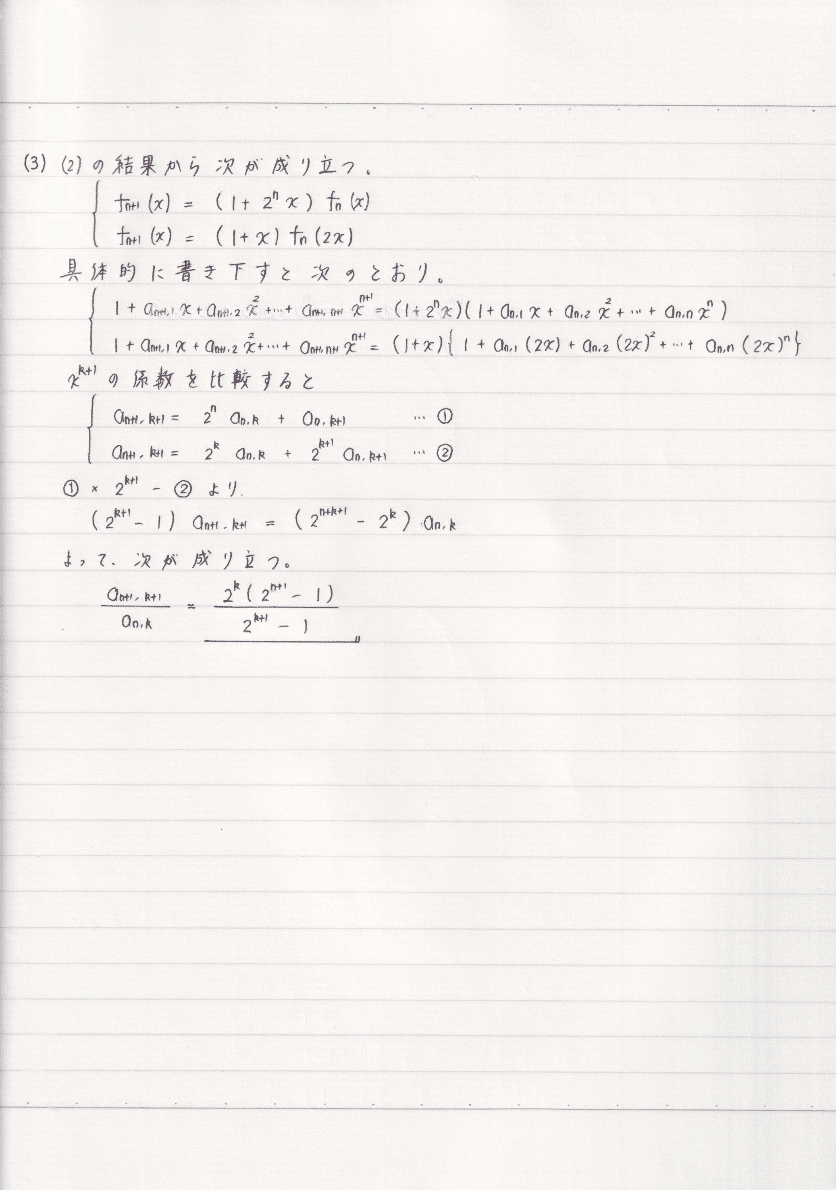
解説
まず(1)です。$${a_{n, 2}}$$とは、$${2^0, 2^1, 2^2, \dots, 2^{n-1}}$$の$${n}$$個から2個選んで積をとり、その積をすべての選び方について足し合わせたものです。
ところで、次の展開式を考えてみましょう。
$$
\begin{array}{}
(x+y)^2&=&x^2+y^2+2\underline{xy}\\
(x+y+z)^2&=&z^2+y^2+z^2+2(\underline{xy+yz+zx})\\
(x+y+z+w)^2&=&x^2+y^2+z^2+w^2+2(\underline{xy+xz+xw+yz+yw+zw})
\end{array}
$$
下線部を確認してみると、各文字から2個選んで積をとり、その積をすべての選び方について足し合わせたものになっています。このことを利用します!$${a_{n, 2}}$$を考えるためには、次の展開式を考えればよさそうです。
$$
(2^0+2^1+2^2+\dots+2^{n-1})^2=(2^0)^2+(2^1)^2+(2^2)^2+\cdots+(2^{n-1})^2+2a_{n, 2}
$$
左辺は、初項$${1}$$、公比$${2}$$の等比数列の初項から第$${n}$$項までの和の2乗となっています。右辺から最後の項を除いた部分は、初項$${1}$$、公比$${4}$$の等比数列の初項から第$${n}$$項までの和となっています。これらから$${a_{n, 2}}$$を求めることができます!
さて、(2)に行きましょう。$${f_n(x)}$$が与えられた展開の形のままでは手も足も出ません。求める分数が$${x}$$についての整式になると言われているので、$${f_n(x)}$$を因数分解したらうまく因数が消えるのではないか?と考えます。
$${n}$$個の中から2つ組、3つ組、4つ組…のそれぞれの積の和が出てくるといえば、次の展開式を思いつくでしょうか。
$$
\begin{array}{}
(x+\alpha)(x+\beta)&=&x^2+(\alpha+\beta)x+\alpha\beta\\
(x+\alpha)(x+\beta)(x+\gamma)&=&x^3+(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x+\alpha\beta\gamma
\end{array}
$$
次数の高い順に係数が、$${n}$$個の中から1つ(組)、2つ組、3つ組のそれぞれの積の和になっています。これをもとに$${a_{n, k}}$$が出てくる形を考えてみましょう。
$${f_n(x)}$$の形も、$${n}$$個の中から1つ(組)、2つ組、3つ組…のそれぞれの積の和が順番に出てきていますが、$${x}$$について昇べきの順に並んでいます。先ほどの展開式は降べきの順に並んでいるので、$${x}$$の係数と定数項を入れ替えてみましょう。
$$
\begin{array}{}
(\alpha x+1)(\beta x+1)&=&1+(\alpha+\beta)x+\alpha\beta x^2\\
(\alpha x+1)(\beta x+1)(\gamma x+1)&=&1+(\alpha+\beta+\gamma)x+(\alpha\beta+\beta\gamma+\gamma\alpha)x^2+\alpha\beta\gamma x^3
\end{array}
$$
こうすると$${f_n(x)}$$の形と似たような形になりました!このことから、$${f_n(x)}$$は次のように因数分解できることが分かります。
$$
f_n(x)=(2^0 x+1)(2^1 x+1)(2^2 x+1)\cdots(2^{n-1}x+1)
$$
この表式を使って$${f_n(x), f_{n+1}(x), f_n(2x)}$$を計算し、求めたい分数式に代入すれば完了です!
最後に(3)です。(2)の結果をまとめると、$${f_{n+1}(x)}$$と$${f_n(x), f_n(2x)}$$との関係はそれぞれ次のようになります。
$$
\begin{array}{}
f_{n+1}(x)&=&(1+2^nx)f_n(x)\\
f_{n+1}(x)&=&(1+x)f_n(2x)
\end{array}
$$
$${a_{n+1, k+1}}$$, $${a_{n, k}}$$はそれぞれ$${f_{n+1}}$$, $${f_n}$$の係数なので、両辺の係数を比較すればよさそうです!$${k+1}$$次の係数を比較するのですが、$${a_{n, k+1}}$$が出てきてしまうので、2式から消去しましょう!
ところで、母関数という言葉を聞いたことがあるでしょうか?ここでは数列の母関数を次のように定義します。
定義1
数列$${\{a_k\}}$$の母関数$${f(x)}$$を$${f(x)=\displaystyle\sum_{k=0}^{n}a_k x^k}$$で定義する。
自分が高3のときの夏の東大実戦模試の第6問で初めて母関数の問題に出会いました。その問題はかなりの難問でしたね。自力で解答を再現するのは愚か、模範解答を理解するので精一杯という感じ。
さて、定義の$${f(x)}$$を具体的に書き下すと、
$$
f(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots
$$
となります。今回の$${f_n(x)}$$は、「$${2^0, 2^1, 2^2,\dots, 2^{n-1}}$$の$${n}$$個の中から$${k}$$個を選んで積をとり、その積をすべての選び方について足し合わせたもの」を$${a_k}$$としたときの母関数となっています!
有名な母関数としては、$${a_k={}_n\mathrm{C}_k}$$とした次の母関数が挙げられます。
$$
f(x)=\displaystyle\sum_{k=0}^{n}{}_n\mathrm{C}_kx^k
$$
これは$${f(x)=(1+x)^n}$$ですよね!つまり、次の等式が成り立ちます。
$$
\displaystyle\sum_{k=0}^{n}{}_n\mathrm{C}_kx^k=(1+x)^n\qquad\cdots(\ast)
$$
この等式$${(\ast)}$$からいくつかの興味深い性質が導かれます。まず、$${x=1}$$を代入すると、次が成り立ちます。つまり、二項係数を右下の文字について和をとると$${2}$$の冪乗になります!
$$
\displaystyle\sum_{k=0}^{n}{}_n\mathrm{C}_k=2^n\qquad\cdots(1)
$$
次に、$${(\ast)}$$の両辺を$${x}$$で微分してみると、
$$
\displaystyle\sum_{k=0}^{n}k{}_n\mathrm{C}_kx^{k-1}=n(1+x)^{n-1}\qquad\cdots(\star)
$$
となります。この式に$${x=1}$$を代入すると、次が成り立ちます。
$$
\displaystyle\sum_{k=0}^{n}k{}_n\mathrm{C}_k=n\cdot2^{n-1}\qquad\cdots(2)
$$
続いては、$${(\star)}$$式の両辺をさらに$${x}$$で微分してみましょう。
$$
\displaystyle\sum_{k=0}^{n}k(k-1){}_n\mathrm{C}_kx^{k-2}=n(n-1)(1+x)^{n-2}
$$
これは次のように変形できます。
$$
\displaystyle\sum_{k=0}^{n}k^2{}_n\mathrm{C}_kx^{k-2}=\displaystyle\sum_{k=0}^{n}k{}_n\mathrm{C}_kx^{k-2}+n(n-1)(1+x)^{n-2}
$$
この式に$${x=1}$$を代入すると、次が成り立ちます。
$$
\begin{array}{}
\displaystyle\sum_{k=0}^{n}k^2{}_n\mathrm{C}_k&=&\displaystyle\sum_{k=0}^{n}k{}_n\mathrm{C}_k+n(n-1)2^{n-2}\\
&=&n\cdot2^{n-1}+n(n-1)2^{n-2}\\
&=&n(n+1)2^{n-2}\qquad\cdots(3)
\end{array}
$$
他にもあったと思うのですが思い出せないので一旦これくらいで。また見つけたらその都度更新します。他にも有名な母関数があるので、気になる方は調べてみてください。今回の問題とは関係ないですが、二項係数も面白いです。
最後にコメント
この問題は正直知識ゲー要素が強いと思います。
(1)の$${a_{n, 2}}$$を求めるのですら経験したことがないと非常に難しいと思います。東大に受かるような人は初見でも解けるのか?(1)は高1の2学期にやった類題が強烈に印象に残っていたので解けましたが(やった時期まで覚えている)。
自分が受験したときは(2)以降はちょっと考えてすぐ捨てました。ここで沼るより他の問題の解答を仕上げる方が点を集められると思ったからです。「捨て問を見極める力」「捨て問を捨てる勇気」が問われますね。
そういうわけで、個人的な難易度は「やや難〜難」です!類題をやったことがないなら難、やったことがあったとしてもやや難はあると思います。しかもこれ文系でも出てるのヤバい。
2020年のセットならこれが一番難しいかな。第6問も結構難しいですが、そちらは(1)が確実にとれる問題なので。ですが、多くの学びを得られる良問だとは思います!他大学でもこれをもとにした類題が出てくるんじゃないかな。
今回はここまで。次回は2020年東京大学理系第5問を取り上げます!
最後までお読みいただきありがとうございました。もしよろしければ、次回以降の記事もお読みいただけると嬉しいです。
それでは、また次の記事で。
2024.02.22
しろ@
この記事が気に入ったらサポートをしてみませんか?
