
楕円曲線とトーラス
前回の続きです。楕円曲線上の点の足し算が不思議なルールだったわけですが、それが実はトーラス(ドーナツの表面)と同型であるという、にわかには信じられない話で終わったのでした。
同型について少しだけ確認します。
たとえば、
{1,-1}に×
{偶数,奇数}に+
{表,裏}に「その状態にする」
などは同型になります。
1×1=1
偶数+偶数=偶数
表を表にすると、初めの状態から見て表
1×(-1)=-1
偶数+奇数=奇数
表を裏にすると、初めの状態から見て裏
(-1)×1=-1
奇数+偶数=奇数
裏を表にすると、初めの状態から見て裏
(-1)×(-1)=1
奇数+奇数=偶数
裏を裏にすると、初めの状態から見て表
良いですね、全部対応しています。つまり
1↔偶数↔表
-1↔奇数↔裏
×↔+↔その状態にする
という綺麗な対応関係があるわけです。そこで、楕円曲線とトーラス上の点との対応関係があるという事実を借りて遊んでみましょう。
トーラスの画像をwikipediaから引っ張ってきました。

いいですね。赤い線がありますが、ここで切断すると、円柱が曲がった形に見えますよね。

そして、赤紫の線で切断すると、円柱が開いて歪んだ紙一枚になります。頑張れば正方形に見えます。

赤い線と赤紫の線はもともとあった位置に対応しています。まあなんという無理矢理な感じもしますね。正方形を曲げて向かい合う辺同士をくっつけるとトーラスになるわけです。なお、南に進むと北から出てきて、東に進むと西からでてくるのは、みなさんご存知、ドラクエ(FFとかでもいい)の世界観ですね。

モンバーバラから南に進むとスタンシアラに着き、スタンシアラから西に進むと海鳴りの洞窟に着き、海鳴りの洞窟から北に進むとパデキアの洞窟に着きます。
つまり、ドラクエの世界はトーラス状の惑星だったわけです。ちなみに、惑星がドーナツ型をしていた場合、内側は無重力状態になることが知られています。どうなっているんだドラクエ世界。
さて、上下と左右の辺がつながっている世界上で足し算を考えましょう。世界の四隅はつながっていますので、ここの点を原点とし、そこからどれだけ進んだか、という量の足し算で表します

はい!windowsの古典アプリ、ペイントで作成しました!ほとんどフリーハンドで数値も目測なので、正確ではありません!それにしてはわりと上手いですよね!
赤い点と青い点を足すと、紫の点になります。座標同士の足し算です。
さて、トーラスの話ばかりしていますが、楕円曲線とどう関係あるのでしょうか?
楕円曲線の式とグラフを再掲します。
![]()

楕円曲線は線が2本ですが、トーラスは平面的です。なので、このままでは完全に対応しきれません。しかし、楕円曲線を複素数にまで拡張すると、しっかりトーラスになります。複素数は視覚的にとらえ辛いので、とりあえず実数のまま遊びましょう。
さて、楕円関数上の点と、トーラス上の点を対応させていきます。1と偶数と表を対応させたように。
ヒントは次の3つ。
無限遠点は単位元(かけ算における1のように、何も変化しない要素)
楕円曲線の右のほうはトーラスのy=0の直線に相当する。
楕円曲線の左側の輪っかは、トーラスのy=0.5の直線に相当する。
さて、ここから頑張って対応を考えます。
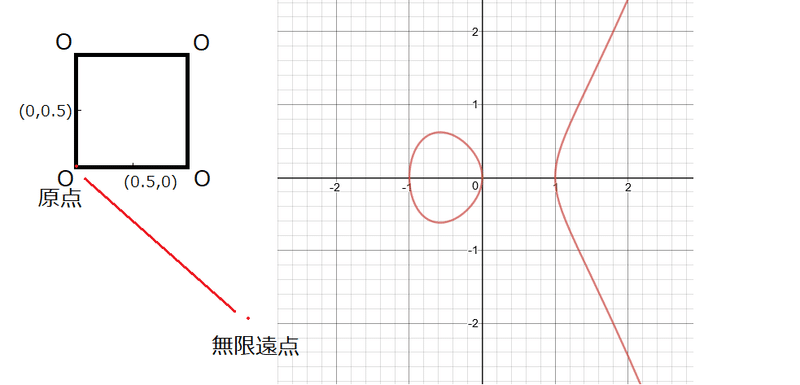
まずは、無限遠点と原点の対応。
さて、トーラス側で二回同じものを足すと原点に戻ってくる点を考えます。
(0, 0) ・・・すでに楕円曲線の無限遠点と対応済み
(0, 0.5)
(0.5, 0)
(0.5, 0.5)
の四つです。この世界においては、1と0は等しいので、
(0, 0.5)+(0, 0.5)=(0, 1)=(0, 0)
となります。さて、楕円曲線上で考えると、二回同じものを足すというのはその点における接線を引くことに相当します。接線を引くと他の点と交わらずy軸方向の無限遠点に到達する箇所は3か所あります。
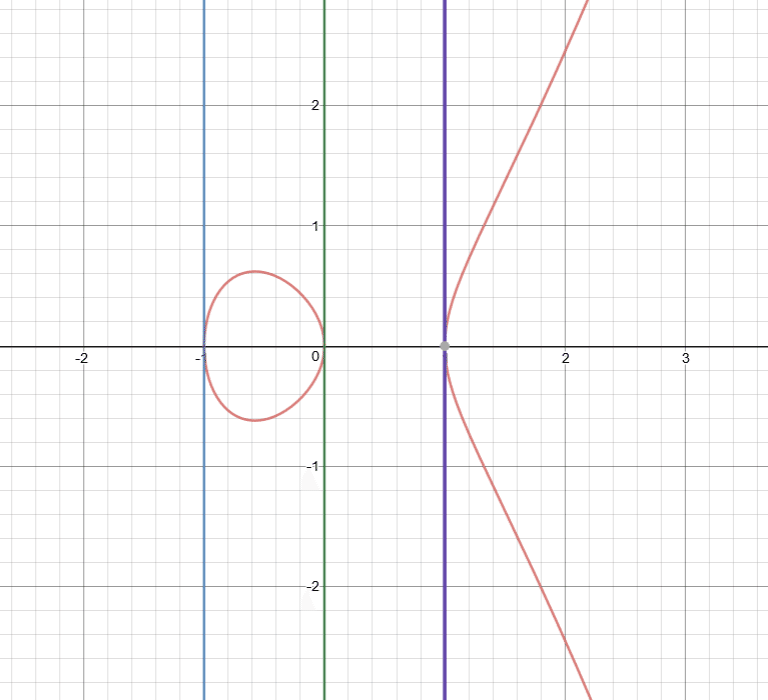
はい、(-1, 0)、(0, 0)、(1, 0)の三点です。・・・早速トーラス側の残りの三つと一致していますね。右側の富士山のほうがトーラスのy=0に相当するので、楕円曲線の(1, 0)とトーラスの(0.5, 0)が対応することがわかりました。

さて、残りの楕円曲線側の(-1, 0)、(0, 0)は、トーラスの(0, 0.5)と(0.5, 0.5)のどちらに相当するんでしょうか。これ、実はどちらに相当しても区別はできなさそうなことがわかるので(解説略)、恣意的に決めてしまいます。楕円曲線の(0, 0)をトーラスの(0, 0.5)に対応させてみましょう。

さて、ちょっとだけ遊んでみます。トーラス側で
(0, 0.5)+(0.5, 0)=(0.5, 0.5)
と計算できます。これは、楕円曲線上で、
(0, 0)と(-1, 0)を結ぶ直線は(0,1)を通る(これはx軸上なので、x軸に対して対称の点を取る必要がない)
となって、見事に一致していますね。なんだかテンション上がってきますよね。でも、まだなんか簡単すぎて感動するというほどでもないので、トーラス上で(0.25, 0.5)という点について考えてみましょう。

この点の特徴は、二回この点について足すと
(0.25, 0.5)+(0.25, 0.5)=(0.5, 1)=(0.5, 0)
となって、下の辺の(0.5, 0)となり、楕円曲線上の点(1, 0)と対応することになります。さて、楕円曲線上で同じ数を二回足す、とは接線を考えるのでした。では、接線が(1, 0)を通るような直線はどのようなものでしょうか。見た目で考えると・・・

ずばり、この二つの直線です!さて、この接点、desmosに計算させると、(-0.414, 0.586)と(-0.414, -0.586)となって、まあ色んな実数の小数展開を記憶している方なら割とすぐに(1-√2, ±(2-√2))だな、と直感が働くと思うのですが、まあそういう方は少数派でしょうし、それに近い値なだけでもしかしたら違うかもしれませんからしっかり計算したいですよね。でも、難しい数学はわからない・・・高校数学まででなんとかわかりたい。
接線といえば、微分です!そう高校で習いましたよね!微分しましょう!
まず、元の式を眺めます。
![]()
う~ん、左辺が二乗されているので微分しずらい。今は実数のみで考えているので、左辺は0以上。ということは右辺も0以上です。なので、そのままルート記号√に入れて正の平方根を取ってしまいましょう。正のyだけ取り出されるので、上半分のグラフになります。
![]()

なぜだか若干興ざめな感じのグラフになりました。さて、(x, y)と(1, 0)を通る直線の傾きはy/(x-1)ですから、y'=y/(x-1)を解けばいいことになります。

これをもとの楕円曲線にx軸に対称な点も含めて図示すると、

んにゃにゃ!?答えが四つ出てきたぞ!なんとびっくり!
と思って、もう一度トーラスの方を確認しましょう。

確かに、二回足して(0.5, 0)になる点は、(0.25, 0.5)のほかに、
(0.75, 0.5)
(0.25, 0)
(0.75, 0)
の三点がありますね。つまり、楕円関数において、接線が(1,0)を通る点は4点あったわけです。見た目は二つにしか見えなかったんですが、式の力は強いですね。トーラスとの関係も強いですね。全ての接線を引いておきます。

どうです、すごいでしょう。思えば右側の富士山は、どの点でも接線が引けて、(1, 0)を除くどの点で引いた接線も、同じく富士山のどこかの稜線にぶつかるようにできている絶妙な曲線なわけですね。(厳密には、変曲点では接線と交点が一致してしまいます。その点はトーラスの(1/3, 0)と(2/3, 0)に対応します。綺麗)
というわけで、トーラスとの完全対応を見ましょう!

わああ、綺麗!ゾクゾクするほど楽しいですよね!
楕円曲線とトーラスの群構造が同型、それは人から聞いた知識であって、証明も何も知りません。でも、高校数学を使って、それを確かめることができる、最高じゃないですか!
微分はもちろんとっても有用で、あらゆる分野に応用が利く素晴らしい数学の概念ですが、こんな風におもちゃとして使ってもとてつもなく面白いものですね。
高校数学はこのような遊びのためだけに手に入れるおもちゃである、という考えも私はそう悪くないと思っています。
最後に、まだ引いていなかった直線を引いて、この同型があまりにうまくいっていることを確かめて、二回に続いた楕円曲線を締めたいと思います。

各曲線の式も同時にお見せします。
あまりにも綺麗ですね!
--ここから先の有料記事ではトーラスの(0, 0.25)に対応する部分を計算してみるおまけです。サポートと同じ感覚でご利用ください--
ここから先は
¥ 100
記事のお読みいただきありがとうございます。 即興演奏を通した様々な活動と、これからの執筆活動のために、サポートしていただけたら幸いです。
