ルドーの「6が出たらもう一度振れる」ルールで1ターンで進める期待マス数は？（解説）

問題はこちら：

答え：4.2マス

　6が出たらもう一度振れるというルールがある場合、1ターンで進めるマス数の期待値は4.2マスになります。ちなみに通常のすごろくの場合は3.5マスなので、6でもう一度振れる恩恵は大きく、その分進行が早くなる事が期待できますね。この期待値がどう算出されるか解説します。

解説：出目とそれが出る確率を掛けて足すと期待値になる

　期待値は「事象の値vとその事象vが出る確率p」を事象すべてについて足し合わせると求める事ができます。日常で良く使ういわゆる「平均（算術平均）」は、各事象の確率が全て等しいとした時の期待値です。　
　
　サイコロは言わずもがなですが出目が1～6まであります。これが事象の値です。そして各出目はそれぞれ1/6の確率で出ます。なので普通にサイコロを振る場合、その出目の期待値は、

となり3.5マスである事がわかります。

　さて、今回の問題は同じサイコロでも「6が出たらもう一度振れる」という追加ルールがあります。これは6＋αの出目があるという事です。ただし6が出たら2回目を必ず振るので、出目として「6」はありません。それらを踏まえて試しにそれぞれの目について具体的な確率を考えてみましょう。

　まず1～5は普通のサイコロと同じで1/6の確率で出ます。6も1/6の確率で出ますが、その場合続けてサイコロを振るため、6という出目になる確率は0。6が出た場合、2回目のサイコロの出目が1～5になる確率も1/6ですが、その合計の出目である7～11になる確率は同時確率なので1/6×1/6=1/6²となります：

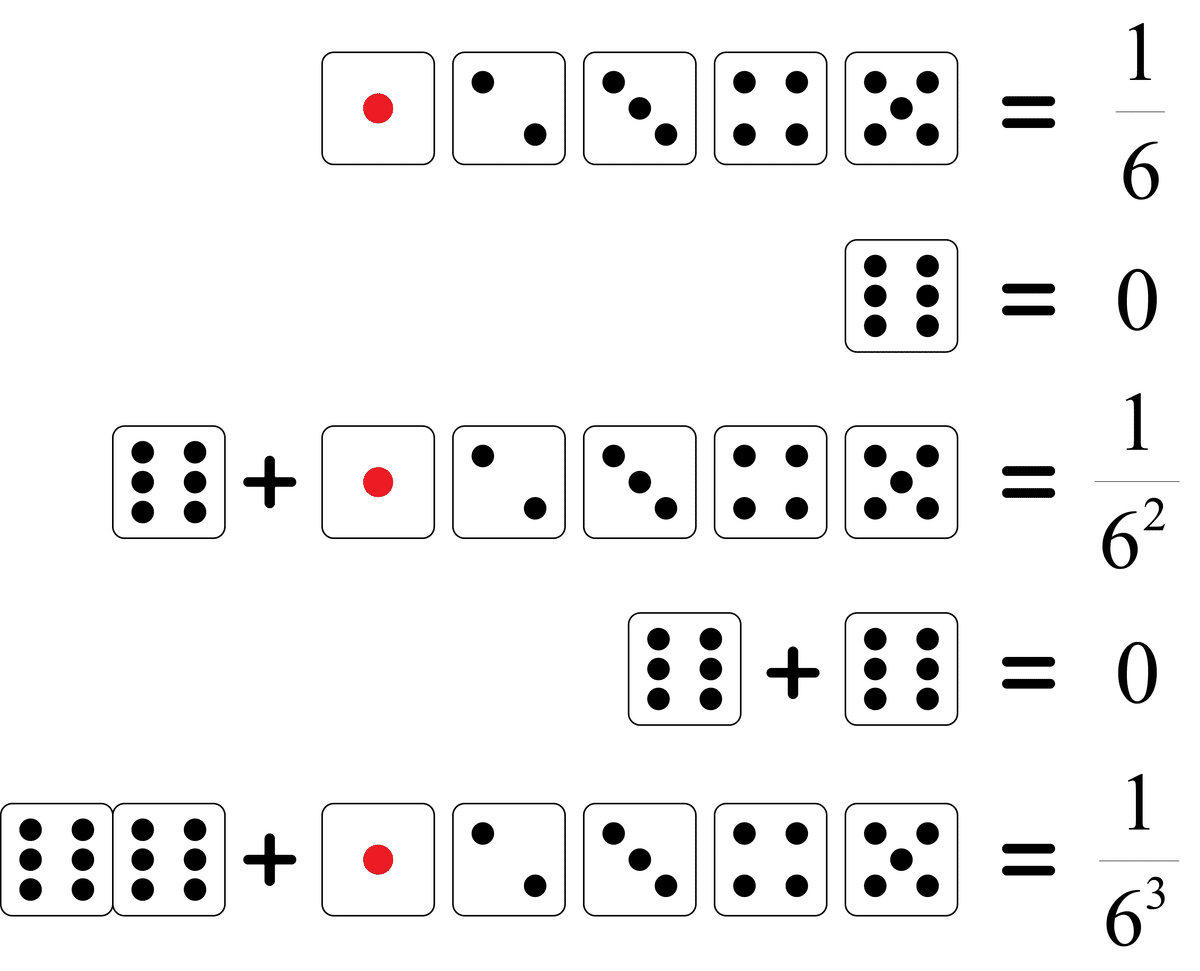
この確率に出目を掛け算して全部足すと期待マス数になります。実際に数式を立ててみましょう：

確率的には凄く低くなりますが、6が出続ける可能性はゼロではないため、100マス進める可能性も、1000マス進める可能性もあり得ます。つまり上の期待値の計算式は無限に続くわけです。

　上の数式の括弧の中はそれぞれ1,7,13…から5つ分の出目を足しています。この法則はこの先の式でも同じです。そして括弧に掛ける確率は1/6の累乗になっています。これらの法則性を踏まえて上式をΣで置き換えてみましょう：

2つのΣ（無限級数の和）に分ける事が出来ました。この無限級数和を次に求めましょう。まず2つあるうちの右側から先に求めてみます。これはいわゆる「無限等比級数の和」で、高校で公式を習っていると思いますが、一応定番の方法で値を出してみます：

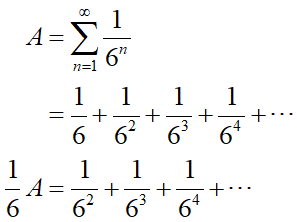
ΣをAと置き、一端ばらして、Aに1/6を掛けた物をAから引き算します：

これによりAは1/5である事がわかりました。ちなみにとても大切な事なのですが、この「1/6を掛けて引く」という作業は本当は「Aが収束する」という条件が必要です。収束しない数列和に対して掛け算して引くという作業をすると計算結果が保障されなくなりますのでご注意下さい（それについては深掘りで）。

　続いて1番目のΣの計算です：

先程と同様にこの無限和をBと置き、いったんばらして、1/6を掛けてBから引き算します。すると、

このように先のAの展開をうまく使えてB=6/25が導けます。これも「Bが収束する」という条件が本当は必要です。

　AとBから期待マス数は、

4.2マスという事がわかりました。

深掘：発散する無限級数の和に対して四則演算してはいけない

　今回の問題で、

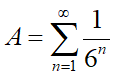
という無限級数の和が出てきました。これは高校で習う「無限等比級数の和」という形になっていて、次のような公式からAを簡単に求められます：

aは0<a<1の範囲にある実数です。a=1/6を代入すれば1/5がすぐに求まります。

　解説ではこの公式は用いずに、Aの両辺に1/6を掛け算してAから引くという作業をしました。おそらく高校でも同じ方法で上の公式を導いたのではないでしょうか？

　しかし、本当はそれは安易に行ってはいけません。その計算が正しくなるには「無限級数の和が収束する」必要があります。今回は0<a<1の時の無限等比級数の和が収束する事が既に広く一般的にわかっている事なので、それを既知として許容しました。

　無限級数の和に対し四則演算する時にどうして収束が必要なのか？その厳密な理由はとても難しい（大学数学のお話）ので、ここでは収束しない無限級数に四則演算を施すとどんな変な事が起こってしまうのか実感する事でその危険性を認識してみましょう。

　次のような自然数の無限級数を考えます：

これが∞に吹っ飛んでいく事はまぁ自明ですよね。ところがやってはいけない操作を駆使するとこのMが具体的な値を持ってしまいます。実際に試してみます。

　まず両辺を2倍してMから引き算してみます：

Mから偶数部分がごっそり抜け落ちるため、奇数のみの足し算になります。まぁ…そうですよね。さらに2Mで引いてみると、

今度は偶数部分がマイナスとして挿入され、上のような式になります。これをTと置きます。これも計算過程としてはおかしくありません。

　上式からTが分かればMも分かるはず。そこで今度はTに-1を掛けてTから引くという作業をしてみます：

1と-1が繰り返す無限級数が出てきました。無限に続く物ですから、無限の先までこの法則は変わらないはず。そこでこれをSと置き、さらにTの時と同じように-Sを引き算すると…

Sの最初の1以外はすべて相殺され、結果S=1/2となりました。Sは1と-1の繰り返しなのに、答えが分数？？もうがっつりきな臭いですよね。このSから、

Tが分かればMもわかるので、

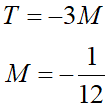
と無限に発散するはずのMの値が定まってしまいました…。

　これは明らかにおかしな事になっていますよね。だってMは自然数を無限に足したもので、どう考えても無限大に発散してしまうはず。仮に収束するとしても自然数の足し算は自然数なのに、上の方法で掛けたり足し引きしたりしたらMはマイナスだし分数だし…。単純に足し引き掛け算をしただけで計算手順としては問題無いのに、何でこんな答えが出てしまうのでしょうか？

　こうなってしまう理由が「収束しない無限級数に四則演算を行う」という事なんです。実は無限級数の和を演算する時にはその配列の足し算の順番を勝手に変えてはいけず、前から順番に足さないといけないという約束があります。それを破るとどうなるか上の計算で出てきたSを例にすると良く分かります：

無限に2個ずつくくって先に計算するとカッコ内は全部ゼロになるので、答えが0にも1にもなってしまいます。もちろんどちらも正しくありません（Sは振動するため答えは定まらない）。SやTやMを計算する時に配列を1つずらして引き算するみたいな事をしましたが、それが変な事になった元凶です。

　「なるほど、じゃあ無限級数の和が収束するかどうかはどう調べたらいいのか？」と言うとですねぇ…これがすこぶる難しいのです。難しいので、高校数学では無限等比級数の和が収束する事を自明として扱っていますし、両辺をa倍して引いて云々という「収束するか分からない物に対してやってはいけない証明」で証明したように見せています。この辺りは正直高校数学の闇です…(-_-;

　今回はサイコロの出目の期待値のお話でしたが、最後は無限級数和の闇のお話に変わってしまいました(^-^;。期待値についてはお話したい事が沢山あるのですが、今回はもうちょっと冗長になってきているので、それは次の機会で。

ではまた(^-^)/