正三角形を囲う最小の正方形は?(解説)
問題はこちら:
答え:


辺の長さ1の正三角形を囲う正方形は、上図のように正三角形の1頂点を角にし、他の頂点までの角度が丁度15°になるようにした時に最小になります。何となくそういう形かなと想像した方は多いのではないでしょうか?ただ、これを証明しようとすると中々大変です。なぜこの長さになり、なぜこれが最小正方形なのかを解説します。
なお以下の証明は僕が導いた一例でちょっと泥臭い印象です。もっとスマートな方法があるような気がしています。思い付いた方は是非コメントで教えて下さい!
「正方形に含まれる最大の正三角形」として考える
この問題、正三角形を囲う正方形を求めようとすると結構てこずります。正方形は頂点が4つあるので、位置や回転などを定義するのが難儀なんです。そこで視点を変えてこの問題を「正方形に含まれる最大の正三角形を求める問題」と読み替えます。こうすると扱う頂点数が減るので式展開が多少楽になります。
とは言っても正方形の中に含まれる正三角形は無数に存在します。最大正三角形が持つ特徴を考えて調べるケースを絞っていきましょう。
最大正三角形の1頂点は正方形の辺上にある
まず正三角形の3頂点がいずれも正方形の内側にあり、辺上に無い状況を考えてみましょう:

この場合、この正三角形よりも大きな正三角形が必ず存在します。正三角形の外心から頂点に向けて放射状に線を引くと、各頂点の外側に拡張する余白があるからです。この余白が無くなるまで、つまり頂点の一つが正方形の1辺に到達するまで大きさを拡張できます。つまり、最大正三角形の頂点の一つは少なくとも正方形の1辺にある事がここからわかります。少し条件を絞れました。
最大正三角形の2頂点は正方形の辺上にある
1頂点が正方形の辺上にある上の赤い正三角形よりもさらに大きな正三角形が存在します:

左辺上の頂点を起点にして正三角形の残り2点に向けて延長線を引くと、外側に余白があるのでより大きな正三角形を描く事が可能です。これはどちらかの頂点が正方形の辺に接するまで拡張できます。つまり、最大正三角形は少なくとも2頂点が正方形の辺上にある事になります。
L字上を動く2頂点で出来る最大の正三角形
という事で、最大正三角形は少なくともその2頂点が正方形の辺上にある事がわかりました。そういう正三角形には以下の3パターンが考えられます:

同一辺型は2頂点が同じ辺に並んでいるケースです。このパターンでの最大正三角形は2頂点が正方形の角にあるケースでしょう:

流石にこれは自明で良いかなと思います。とりあえずこの辺の長さが1のが暫定最大正三角形です。
次にL字のケースを詳しく見て行きましょう:

1辺が1の正方形の左下を原点都市、点Pを正方形のX軸上を動く点、点QをY軸上を動く点とします。PとQの座標はそれぞれ、

です。これを底辺とする正三角形を描き、残りの頂点をRとします。
点Rは正方形の内側になければならないので、その成分(Rx,Ry)はそれぞれ以下の範囲になります:

この点Rの座標を点PとQで表現してみましょう。辺PQの中点Aは、

です。この点Aから引いた辺PQに垂直な線上に点Rがあります。そして正三角形なのでARの長さはPQの長さの√3/2倍です。
垂線を表現するため、まずはベクトルPQを算出します:

ベクトルPQに垂直なベクトルをベクトルnとすると、次のようになります:

2次元のベクトルの垂直ベクトルを求めるには「成分を入れ替えてどちらかの符号を反転」です。入れ替えた後にx成分の符号を反転すると元のベクトルの左側に、y成分のを反転すると右側に伸びるベクトルになります。今回はベクトルPQの右側と定義しました。
ベクトルPQとnは成分の絶対値が等しいので、その大きさも等しいです:

点Aとベクトルnから点Rの座標は以下のように求められます:

ベクトルnをその大きさで割ると単位ベクトル(長さが1のベクトル)になります。Aを起点にそれに正三角形の辺の長さPQを掛けて、それを√3/2倍すれば点Rに届きますよね。||n||=||PQ||である事に注意すれば1段目の大きさの項が相殺されて、下段のシンプルな式になります。
さて、点Rの各成分(Rx,Ry)はそれぞれ0~1の範囲に入っていなければなりません。ここからL字パターンの問題は、

このように「a,bの取りうる範囲と条件が決められている時に正三角形の辺の長さLを最大にするa,bを求めよ」という問題に帰着します。解くのにちょっと難儀しますが、方法を見て行きましょう。
まず1段目のRxの範囲となる不等式からRxの範囲条件を満たす(a,b)を求めます。その為に不等式を展開してbの範囲を抽出しましょう:

式の最後、左辺はaのどの範囲でも常にマイナスなのでbの最小値はaの値によらず0になります。一方bの最大値である右辺はaの値により場合分けが必要です:
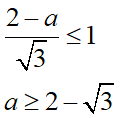
aが2-√3より小さい時は右辺は1以上になるためbの最大値は頭打ちの1、しかしaがそれ以上の場合は右辺が1以下になるため、bの最大値はaの式で表される値に限定されます。まとめると:

このaとbの範囲をグラフに描いてみましょう:
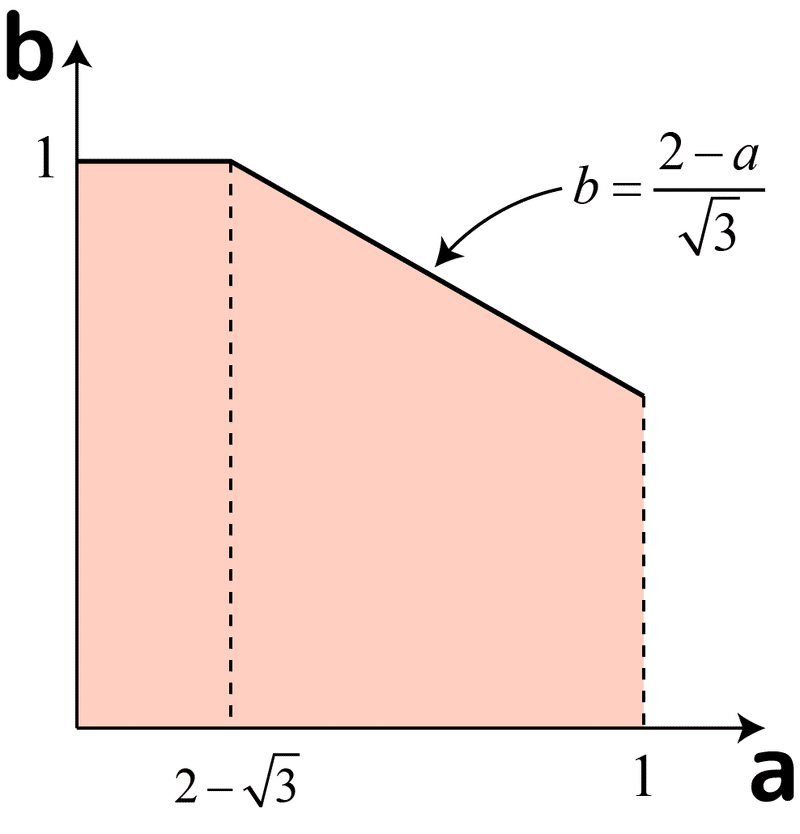
この色が付いている領域が0≦Rx≦1を満たす(a,b)です。ただ、この範囲にあってもRyが0~1の範囲になるとは限りません。そこでRyについても同じようにその範囲を満たす(a,b)を求めてみます:

bの最大値はやはり場合分けが必要です。aが1/√3以下の時はbの最大値は1ですが、それ以上の場合はbの最大値はb=2-√3aと1未満に目減りします:

このRyの領域を満たす(a,b)を先程のRxのグラフに重ねてみましょう:

Rx、Ryそれぞれの条件を満たすのは上の色が付いた領域です。2か所折れている所があり、そこでbの最大値のグラフが変ります。
後はこの領域にある(a,b)からL=√a²+b²の最大値を求めるだけなのですが、ルートがあると面倒なので、代わりにL²=a²+b²の最大値を求めます。
L²の式はこうなっていて、

aが何か固定した値の時にはbがより大きい程Lは大きくなりますよね。つまり先の領域の上端が最大となる(a,b)の候補になります。
0≦a≦2-√3の範囲ではbの最大値は1なので、

単調増加なaの2次関数になります。つまりa=2-√3で、
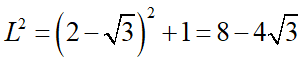
がこの範囲での最大値です。
2-√3≦a≦√3-1の範囲はRx側の直線式を採用です:

展開するとやはりaの2次関数になり、こちらはa=1/2の時に最小値となるので、aの範囲の両端のどちらかに最大値があります:

結果はどちらも同じ最大値になりました。
最後√3-1≦a≦1の範囲はRy側の式を採用です:

こちらも下に凸の放物線で、最小値がaの範囲内にあるので両端のどちらかに最大値があります:

これもどちらも同じ最大値を取るのがわかりました。以上の3つの放物線をグラフに描いてみます:

0≦a≦1の範囲で最大値がこんなにも変化するんですねぇ。結果としてL²の最大値はグラフの折れた個所とa=1の3か所あるのがわかります。それぞれ(a,b)を書き下してみます:

この時いずれも、

うまい事2重根号をはずせてL=√6-√2となり、これがL字パターンでの最大正三角形になります:

いずれも3頂点が正方形の辺上に位置し、その内一つが正方形の角にあるのがわかります。
中々面倒な場合分けでした…が、これで終わりではありません。次は3パターン目の対辺型も同じように調べないといけません。シンドイですが頑張りましょう(^-^;。ただ、細かい所はもう同じなので端折りますね。
対辺を動く2頂点で出来る最大の正三角形
L字型と同様に点PをX軸上を動く点、そして点Qを対辺上を動く点とします:

やる事はL字型の時とほぼ一緒で正三角形の頂点となる点Rをaとbで表します。PQの中点AとベクトルPQ、ベクトルPQの垂直ベクトルnはそれぞれ、

です。ここから点Rは、

このように表現できます。
Rxの範囲からbの範囲をaで表します:

aの範囲によって右辺が0より小さくなるので場合分けをします。結果だけ書き出すと、
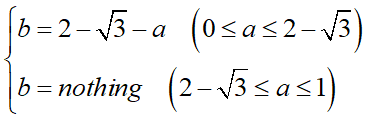
aが2-√3より大きくなるとbがどこにあってもRx>1になってしまうため、有効な(a,b)はありません。
同様にRyの範囲からbの範囲をaで表します:

左辺の最小値はa=1/√3で0境界があり、右辺はa=1-1/√3で1境界があるので、それぞれ場合分けが必要です。全部まるっと考慮するとbは次のようになります:
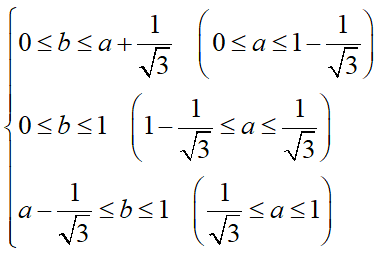
そしてRx、Ryがそれぞれ有効になる(a,b)の領域をグラフにするとこうなります:

Rx、Ry両方の条件を満たすのはRxが存在できる左下の小さい範囲のみである事がわかりました。ここから正三角形の辺の長さLのべき乗が最大になるaを求めます。対辺型の場合Lは、

こういう式になり、ルートの中に(b-a)という差のべき乗があります。という事はL字型と違いあるaに対して常に最大となるbを取れば良い…という訳でもなくなります。aが大きい場合はbを小さくした方が差が大きくなる場合もあるわけです。その分水嶺をグラフに描き込むとこんな感じになります:

青いラインはbの最大値からaを引いた位置をプロットしたものです。この青いラインを境に下はb=0、上はb=2-√3-aののどちらかが候補になり、より距離の長い方が採択されます。各aについて採択されるのが赤いラインで示しているbの値です。グラフからaが(2-√3)/3より小さい間はbの最大値を、それ以上ではb=0を選択するとLはそのaで最大値になれます。
という事で、その範囲でのL²のグラフを描いたのがこちら:

色々細かい事を考慮しましたが、結局のところa=0とa=1の時にそれぞれ同じ最大値を取り、

とL字型の最大値と同じになりました。最大値の時(a,b)=(0, 2-√3), (2-√3,0)です。:

結果的に、L型対辺型いずれも頂点の一つが正方形の角に位置し、残りの頂点が向かいのL字辺上に位置するというのが最大正三角形になりました。そしてそのすべての正三角形の辺の長さLは、

となる事がわかりました。
ここで今回の問題に立ち返ります。問題の正三角形の辺の長さは上のLではなくて1です。そこで上図の正三角形の辺を1とした時の正方形の辺の長さを比例で求めます:

という事で答えは上のようになり、最小正方形の辺の長さはおよそ0.966で正三角形の辺の長さ1よりも短くなる事がわかりました。そして、この値はずばりcos(15°)でもあります:

終わりに
ある図形を囲う最も小さい図形を求める事を「最小境界問題」と言います。囲う図形の事を境界図形と言い、これが回転しなければそれを得るのはそれ程難しくは無いのですが、回転を許すと途端に非常に難しい問題になります。
形状が複雑な図形を単純な境界図形で近似する事で、例えば倉庫に物を詰める時の最適な詰め方を検討しやくすくなったり、ゲームの世界ではワールドに存在するあらゆるものとの衝突を取る時の計算を速くする事ができます。もちろんそこには幾何学的な数学が沢山用いられています。そういう最適化が私達の生活をより便利にしているんですね。
ではまた(^-^)/
この記事が気に入ったらサポートをしてみませんか?
