100個の段ボールを移動する猫を探す最悪手数は？（解説）

問題はこちら：

答え：196回

　100個並ぶ段ボールの中でまったりしつつも移動している猫ちゃんを見つけるのにかかる最悪手数は196回です。これをどう算出するか解説します。

解説：猫が最初偶奇のどちらかに入っていると「仮定」する

　今回の問題、やみくもに箱を開けても埒が明きません。例えば番手の低い段ボールからしらみ潰しに調べようと1番の箱を開けて、猫が移動後次に2番の箱を調べたとします。この時猫が最初2番にいて、次に1番に移動すると、猫はまんまとチェックを通過してしまいます：

（以後視認しやすいよう閉じた箱にいる猫ちゃんを上のように表記します）

　このため端から順に100番まで調べていっても、猫を発見できないケースはいくらでも生じてしまいます。策を講じないと毎回が「猫が100個の箱のどれかに入っている」という最初の状況と一緒で、それだと偶然当たらない限りこの作業は永遠に終わらないんです。

　ですから箱をチェックする度に「猫がいる箱が限られる」「猫がいない箱が確定する」という猫を追い詰める戦略を見つけないといけないんです。この問題の肝はそこです。

1個飛びに猫がいるなら追い詰められる

　100個すべてのどこかに猫が入っている場合、次に猫が移動してもやはり100個のどこかです。これだと状況は一向に好転しません。そこで、仮にですが「猫が1個飛びのどこかにいる」としたらどうでしょうか？要は偶数番にいる、もしくは奇数番にいるという事です：

　例えば上図のように最初偶数番のどこかに猫がいるとします（どこにいるかは不明なので少し猫を薄く表しています）。ここから最初に端の2番を確認します。今最悪手を考えるので残念ながら猫は見つかりません：

でもこの端を確認した時点で「1,2,3に猫がいない」という事が確定します。もちろん最初の仮定の下でですが。

　一つ番手を進めてみましょう。上の状態から猫ちゃんに一つ動いてもらいます：

　先のチェックで1,2,3に猫がいないのは確認済みなので、奇数番に移動した猫の最小番数は3番となります。そこでやはり端である3番を確認します。最悪手ではここにも猫はいないので、この時点で「1,2,3,4に猫がいない」が確定です：

　こうすると、一つ前の状況より猫がいない箱が一つ増えましたよね。また猫が移動したら今度は4番、次は5番と昇順に調べていく。この戦略によって猫を右へ右へ（番手の多い箱へ）徐々に追い詰める事ができるんです。

　今回の問題では段ボールは100個あります。上の追い詰めを続けていくと最後はどうなるか？99番の段ボールで猫が見つかります：

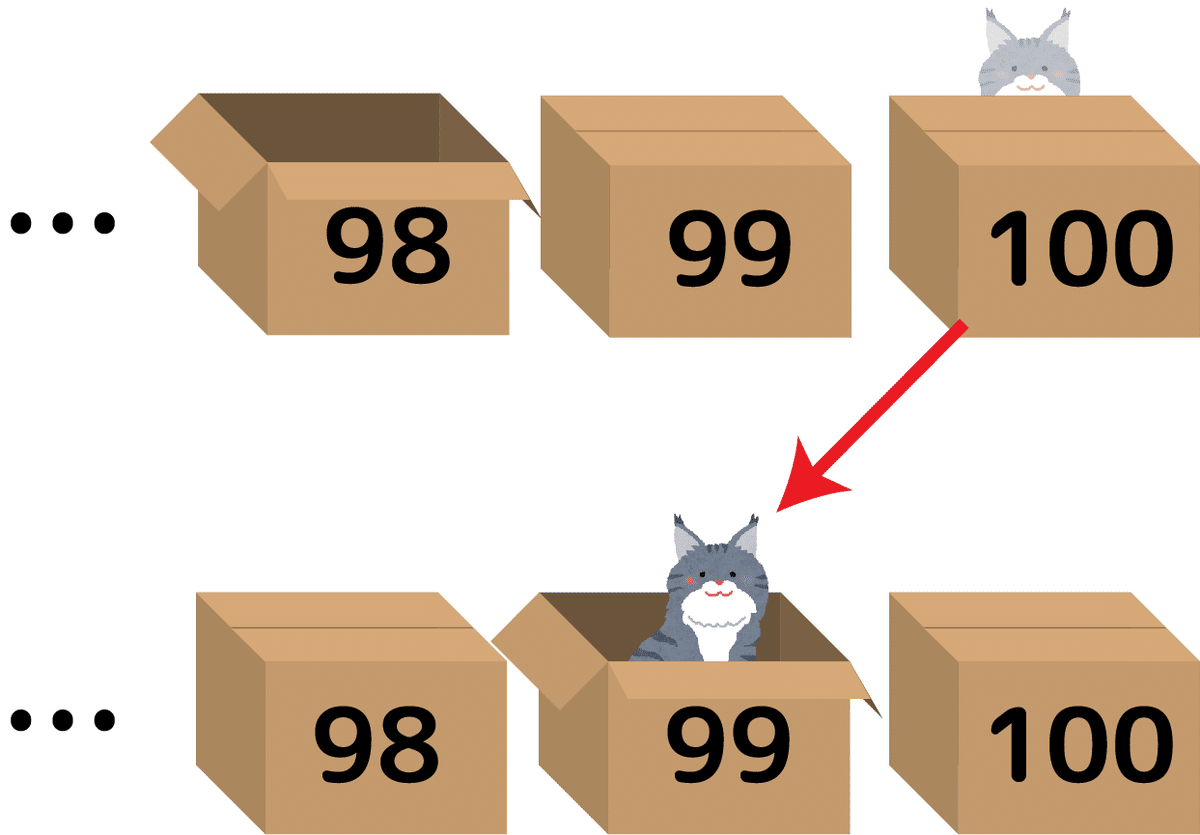
　最後から3番目である98番の段ボールをチェックした時、1～99までいない事が確定します。よって猫は一番右端の100番の段ボールのみに潜む事になります。すると次の手順で99番の段ボールに移動した猫をちょうど発見できる形になります。

　初手で猫が偶数番に潜んでさえいれば上の手順で有限回数で発見できます。

99番まで進めて猫がいなかったら初手で奇数番に猫がいた事が確定する！

　猫が初手で偶数番目に潜んでいて、こちらも偶数番の2番からチェックを始めると、99番の箱で猫が見つかります。しかし、もし猫が最初奇数番に潜んでいたらどうなるでしょう。2番をチェックしている時は奇数番に猫がいて、3番をチェックしている時は偶数番に潜んでいる…とチェックする箱と猫がいる箱の偶奇に掛け違いが起きてしまいます。この場合最後は下図のような関係になり、99番の箱を開いてもそこに猫はいません：

　初手で猫が奇数番にいる場合、冒頭で例に出したようにしらみ潰しチェックの隙間を通り抜けてしまうため追い詰めに失敗してしまうんですね。でもこれで落胆してはいけません。むしろ99番に猫がいなかったという事実から、もっと大きな事実を確認できたんです。そう最初の仮定が間違っていた、つまり「最初に猫は奇数番にいた！」という確定的な事実です。ある仮定の下で手順を進めていたら矛盾が生じた。だから仮定が間違っている。そう、これは数学の背理法です！

　それと同時に、初手ではなく今猫が偶奇のどちらにいるかも判明します。上図のように奇数である99番を開いた時点で、猫はその背反である偶数番のどこかにいるんです。

　99番を開いた後の番手で猫は奇数番のどこかに移動します。と言う事は、こちらも改めて奇数番の端っこから再度チェックしていけば、今度は掛け違いなく偶奇が揃い、確実に猫を追い詰めて最後で発見できます：

　この時上のように1番から昇順にチェックしていくと右端の99番で発見できますが、ちょっとだけ手数を稼ぐなら99番から降順にチェックしていくと2番で猫が見つかります。こちらの方が1手だけお得になります：

試行回数を数えよう

　アルゴリズムが固まったので具体的な試行回数を算出しましょう。まず100個の段ボールの2番から昇順に99番までチェックしていきます。ここまでで100-2=98手。ここで猫がいなくて猫が初手で奇数番にいた事が判明。次は99番から降順で2番までチェックしていき、2番で猫が見つかります。これも同様に98手。2回のチェック作業を合わせると最悪手数は196手となります。

深堀：段ボールがN個の時の最悪手数

　ちょっとだけ深堀します。段ボールがN個の時の最悪手数はどうなるでしょうか？解説でほぼ答えを言っていますが、最初2番からN-1個まで昇順でチェックする事で猫が初手偶数番にいない事が判明するので、ここまででN-2手です。

　N=100の場合、2回目は99番から降順に2番までチェックしました。もし段ボールの個数Nが奇数の場合、例えばN=99の場合、最初のチェックは2番から98番まで行います。最悪手の場合その時点で猫は奇数番にいるので、次からの再チェックで猫は偶数番にいる事になります。つまりまた2番から98番までチェックすれば良いんです。

　Nが偶数の時は2回目は降順で、Nが奇数の時は2回目も昇順でチェックすれば、どちらも、

上式の回数が最悪手数となります。ただしNは3以上です。N=1の時はもちろん1手、N=2の時は片方を確認していなければ猫が移動後もう一度同じ箱を確認すれば見つかるので2手です。

　解説及び深堀のアルゴリズムが最適かと言うと、今回その証明をしていないため厳密にはわかりません。ただ少なくとも一つ確認する度にチェックしなくて良い箱の数を増やしていかないといけなく、そのためには端から猫を追い詰めるしか無いと思いますので、最適に近いアルゴリズムにはなっているように思います。もし今回の解説よりもっと最悪手数が少なくなるアルゴリズムを発見したら、是非SNS等で公表して下さい！

　ではまた(^-^)/