あまりに難し過ぎた伝説の図形問題（解説）

問題はこちら：

答え：5.5cm

　図のxの長さは5.5cmになります。なぜそうなるかを以下で解説しますが、算数の範囲でこれをノーヒントで導くのは本当に難しいです。まずはその算数の範囲で解く方法を、その後に中学数学の範囲での解き方、高校数学の範囲での解き方をそれぞれ解説します。

算数の範囲で解く

　図を見た時、使えそうな特徴が2つあるのがわかります。一つは底辺が2等分されている事、そして∠ADCが135°の有名角になっている事です。

　底辺2等分は頂点から中点に線を引いて三角形を2つに分けた時、双方の面積が同じになります。今回の問題で⊿ABCの面積が15cm²と示されているので、⊿ABD=⊿ADC=7.5cm²である事がわかります。

　算数の範囲で有名角は45°と60°で、いずれも直角三角形にあるとその辺の比がわかります。逆に言うとこれらの角度が問題にある時に直角三角形を探したり補助線を引いて作ったりするのが解き方のセオリーです。

　そこでまず頂点から底辺に向けて垂線を下ろし、その交点をEとします：

すると三角形AEDが直角二等辺三角形になるのでAE=EDが作れます。また⊿ABEと⊿AECも直角三角形になります。

　さてここからがおそらく知っていないと閃けない所です。この問題は面積が絡んでいます。算数の範囲で「直角三角形」と「面積」と言うと、ある定番テクニックが思い当たります：

　面積がS緑の直角三角形を4つ上図のように配置すると、1辺がaの正方形を作る事ができ、その面積もa×aで計算できます。そしてその内側にも青色で示した正方形ができます。この青い正方形の面積S青は外側の正方形の面積（a×a）から直角三角形4つ分の面積を引いたものになるので、aとS緑があればその面積を計算できます。正方形の面積がわかれば、そこから内側の正方形の1辺の長さも求められます。ただし小学生は平方根が使えないので、問題として出される場合はこの辺の長さが手計算でも求まるように調整されます。

　先程の図にも直角三角形が3つあるので、このテクニックを利用できないかなと考えます。そして、3つある内で使えそうなのは唯一斜辺の長さが9.5cmと分かっている⊿AECかなぁ…と想像するわけです。それを適用した図がこちら：

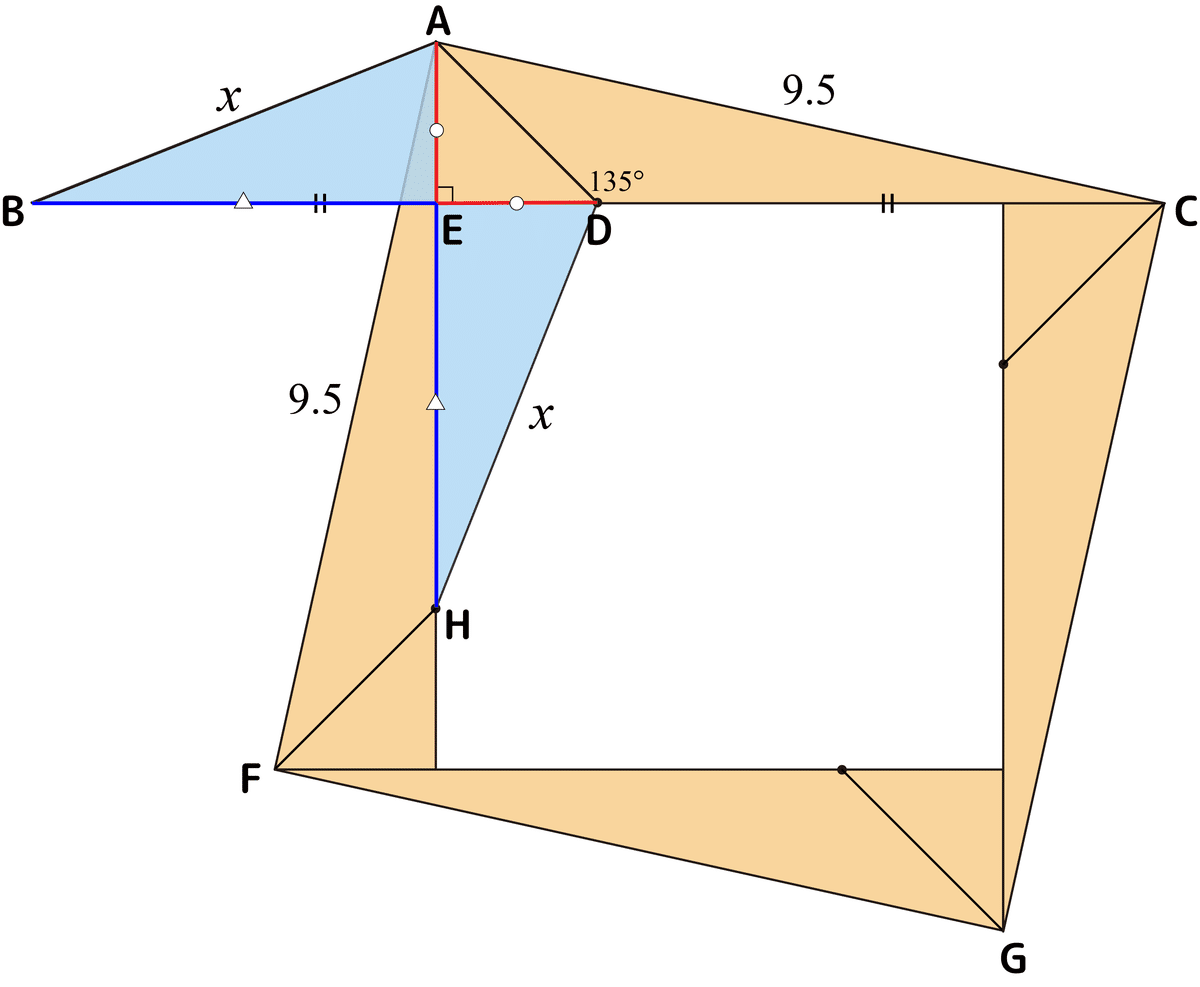
　この問題の最大のポイントがここで、⊿AECだけじゃなく⊿AEDも一緒に含めて先のテクニックに当てはめてしまうんです。この閃きが難し過ぎます(^-^;

　四角形AFGCは正方形で、一辺が9.5cmなので面積は90.25cm²です。ここで⊿EHDと⊿ABEに注目します。これらが直角三角形なのは自明ですね。また⊿AEDが直角二等辺三角形なのでAE=EDです。そしてBD=AHからBE=EHもわかります。ここから⊿EHDと⊿ABEは合同である事が判明します。つまりABと同じ長さがDHに出て来るんです。

　この対応を他の所オレンジの直角三角形にも施すと下図のようになります：

ここで⊿ABCの中にオレンジの直角三角形AECと青い三角形ABEが分かれて含まれている事に注目します。つまりオレンジ＋青＝15cm²です。

　図の1辺が9.5cmの一番大きな正方形の中にはオレンジの直角三角形と青色の直角三角形がそれぞれ4つずつ含まれています。と言う事はそれらを合計した面積は、15×4=60cm²と具体的に計算できます。ここから内側にできた一辺がxの一番小さい正方形の面積Sは、

と求める事ができます。正方形の面積がわかればしめたもので、ここからxの長さは5.5cmと逆算できます。ここがちゃんと逆算できるようにこの問題はできているので算数の範囲で解けるんですね。

　ここまでの過程を限られた時間で閃く事は非常に難しいですよねぇ…。流石ジュニア算数オリンピック伝説の問題です。

中学数学の範囲で解く

　中学数学では平方根や方程式を習うので、三平方の定理や連立方程式が使えます。存分に使いましょう(^-^)

　上図のように補助線AEを引き、その長さをhとします。⊿ABCの面積は15cm²ですが、展開する時に冗長になるのでSと置きます。すると、

と表現できます。

　次に直角三角形AECから三平方の定理より、

がわかります。ここでhy=Sだった事を思い出して代入すると、

となります。右辺は今具体的な数字である事に注意です。

　次にxにからむ直角三角形ABEに注目し、こちらも三平方の定理を適用してみます：

右辺にある2h²+y²は先の式の左辺そのものですよね。それを代入すると、

こうなります。S=15cm²だったので、

このように算数範囲の時のような技巧的な操作をしなくてもxが求まります。

高校数学の範囲で解く

　高校数学になると三角形に纏わる武器が格段に増えます。特に三角関数の威力は絶大です。

　三角形の面積は2辺とその挟む角度が分かれば、

上式で求める事ができます。これを踏まえて問題を見てみましょう：

　⊿ABCの面積をS=15cm²と置きます。ここから⊿ADCと⊿ABDの面積はそれぞれS/2です。⊿ADCは2辺とその成す角度があり、先の公式から面積が求まりますので、式を展開してみます：

このようにaとyを掛けた値が具体的な数値で算出できます。

　次に余弦定理を持ち出します。⊿ADC及び⊿ABDそれぞれで余弦定理より、

これらが成り立ちます。右辺にあるayはもはや単なる数字なので、残るa²+y²を消したい。有難い事に双方にそれが含まれているので、上から下を引き算すると、

右辺に数字であるayのみ残り、式はxについての単なる方程式になりました。ayを戻してあげると、

xが5.5cmと求まります。

閃くために学校の勉強を頑張ろう

　見た事や経験した事が無い問題を解決する時に「閃き」はある程度必要になります。ただその閃きというのがゼロからいきなりポンっと出る事は極めて稀です。多くの場合、「閃き」というのはそれまで培ってきた知識と経験が複合して起こります。三角比を知らない小学生が余弦定理をいきなり思い付くなんて事はまず無いわけです。補助線の閃きも「ここに引けば45°が作れそうだ」とか「こう引けば面積が半分になるな」のように、45度の直角二等辺三角形や面積2等分などの基礎的な性質を知っているからこそ「そう引こう」と閃けるんです。

　数学を含む学問は勿論の事、日々の営みや社会生活で起こる複雑で厄介な問題を解決する時にもこれは同じ事が言えます。「こうやれば問題を解決できそうだ」という思い付きや閃きが起こるには、そもそもにその問題に含まれる基礎となる知識と経験が必要なんです。

　とは言ってもです。学校のテスト問題ならパターンが限られていそうですが、社会生活で起こる問題なんて多種多様過ぎて、閃くのに必要な知識や経験なんてわからないですよね。ここです！だから「学校で様々な分野の基礎を勉強する」んです。人生で何が起こるか分からないのであれば、何が起こっても大丈夫なように、解決までの道筋を見い出せるように、色々な知識と経験を身に付けよう。これが学校で勉強する理由なんです！

　だから皆さん学校で沢山学んで、沢山経験して下さい。勉強は確かに大変ですし面倒くさいですが、それが皆さんのこれからの人生で起こる様々な問題を解決する「閃き」を起こすのに必要な事なんだと知れば、勉強をする意義とか目標もより明確になるはずです。

ではまた(^-^)/