放物線な籠にはまるボールの半径に見られる美麗な関係（解説）

問題はこちら：

答え：ボール1が半径1、ボール2が3、ボール3が5

　問題の条件で籠の中に入るボールはボール1が半径1、ボール2が3、そしてボール3が半径5になります。ここから推測できるように、実は4個目以降も半径が7、9、11…と奇数整数になります。放物線は曲面なのにボールの半径は整数。何とも神秘的です。

　まずは1～3個目の半径を計算してみて、深掘りでそれが整数解になる理由を解説します。

解説1：ボール1の半径は重解がポイント

　まずはボール1の半径を求めてみましょう。ボール1は放物線な籠の底に接する最大サイズのボールです。この意味をまずは把握しましょう。

　そもそも、ボールがすっごく小さかったら籠の底に接地するのは何となくイメージ出来ますよね。一方でボールがある程度大きくなってしまうと、ボールの真下が底に付く前に籠の縁に引っかかってしまいます：

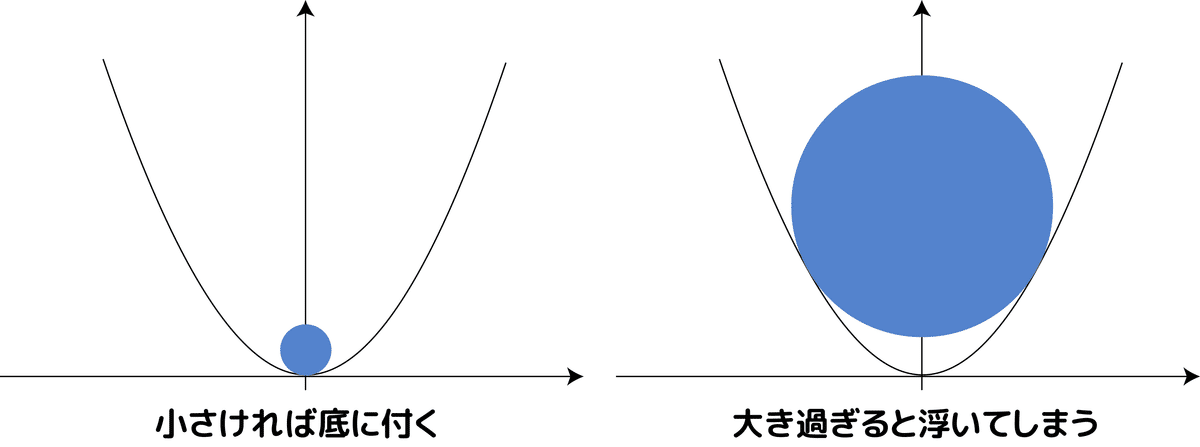
つまりボールの半径を徐々に大きくしていくと、どこかでボールの底が浮く瞬間があるという事です。その半径が最大サイズと言えます。

　ボール1の半径をr1とし、ボール1の真下が放物線の底（原点）に接しているとすると、ボールの中心点P1の位置は、

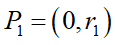
になります。ここからボール1の式は円の方程式より、

と表せます。ボールの底が常に原点にあるため、半径r1が大きくなる程ボールの中心点がその半径分高くなる事が式から分かりますね。

　一方ボールは籠の内側である放物線、

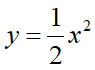
とも常に接します。接する（交わる）というのは放物線上の(x,y)とボール1の円上の(x,y)が共通しているという事なので、ボール1の式と放物線とで連立方程式を立てると交点(x,y)が求まります。放物線の式を、

としてボール1式のx²に代入します。yについて整理すると、

因数分解できる形になります。ここから式を満たすyは、

である事がわかります。y=0の方は原点ですね。これはボール1が放物線の底に接しているので明白です。一方のy=2r1-2は別の交点のy座標です。ボール1が大き過ぎると原点以外にこの交点が生じます：

　今ボール1は籠の底にのみ接っするという条件なので、上図の円の半径を小さくしていき2つの交点を下げていって、それらが原点で重なれば（重解になれば）条件を満たします。つまり、

ボール1の半径r1が1の時2つの交点が原点で重なります。

解説2：ボール2、ボール3の半径も重解がポイント

　ボール2の半径もボール1と似たような手順で導けます。違うのは2個目のボールが1個目のボールのてっぺん、そして籠の縁の2点で接するという事です：

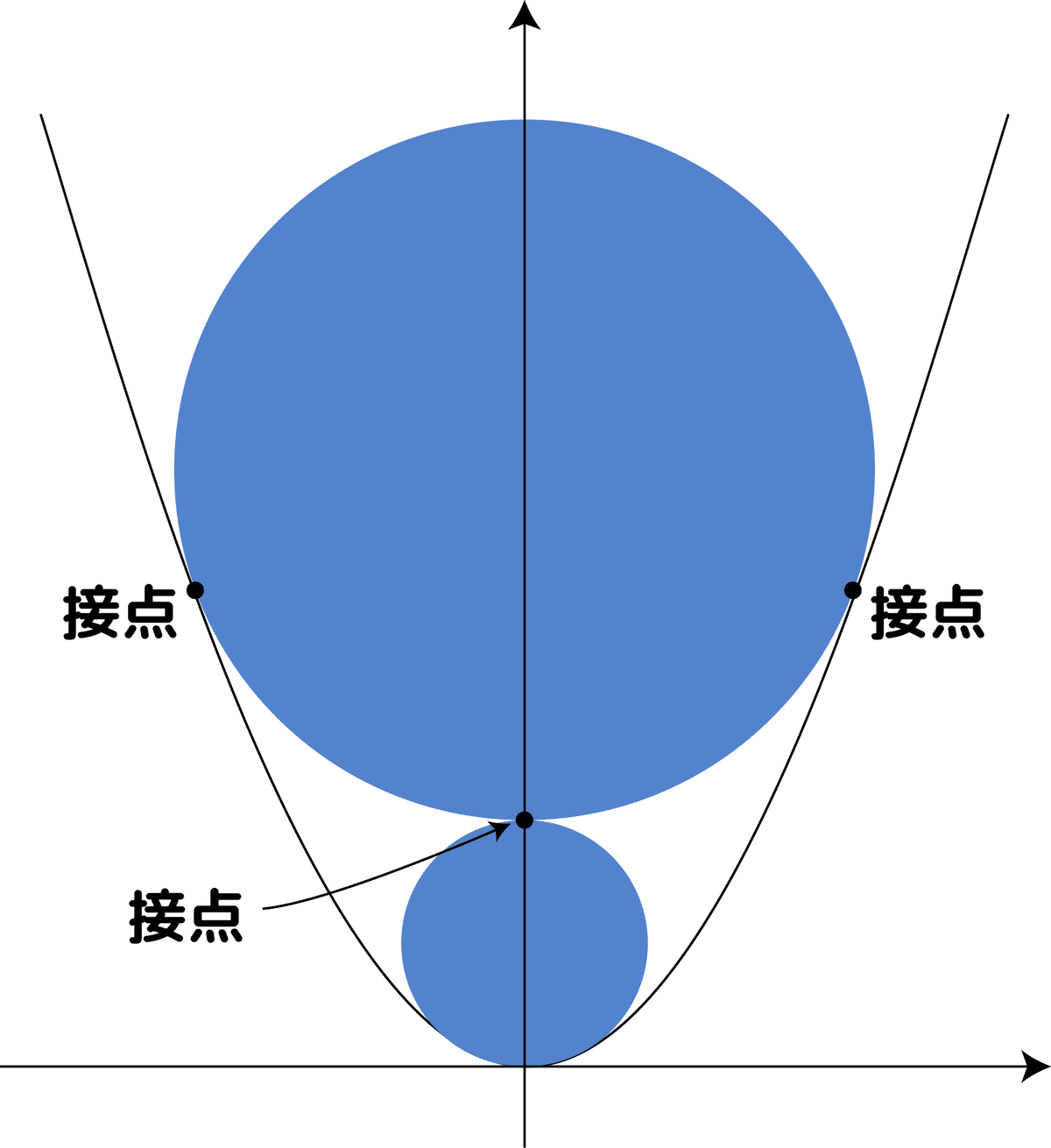
　ボール2の式を立てます。ボール1の半径が1である事から、ボール2の半径をr2とするとその中心点は(0, 2+r2)になります。ここからボール2の式は、

となります。これでボール1との接触は保障です。ボール2は放物線とも接するので同様に、

をボール2式に代入しyについて整理します：

yの2次式なのでyが2つ出てくる事になります。これは下図のようにボールが4点で交差する時の2つのy座標を指しているんです：

今回ボール2は放物線に接する条件です。上図の大き過ぎるボール2の半径を小さくしていくと左右の点はそれぞれ近寄っていき、接する所で一つのy座標のみになります。それは重解であるという事と同意です。2次方程式が重解を持つというのは判別式がゼロであるという事なので、先の式の判別式を書き出してみましょう：

r2のみのシンプルな2次方程式になりました。これはすぐに解けますよね：

r=-1は無いので、ここからボール2の半径r2が3である事がわかりました。

　ボール3の半径もボール2と全く同様の手順で求められます。詳細を省いて式だけで展開すると、ボール3の式は中心点が(0,8+r3)なので、

放物線を代入してyについて整理して、

判別式が、

こうなり、r3を求めると、

という事でボール3の半径は5と求まりました。

　ボール1～3まで半径が奇数整数になるという美しい関係が分かりました。そこから中心点の高さも1、5、13と整数になります。放物線は曲線でボールも曲線なのに半径に整数が出て来るのは不思議ですよね。

　ではその不思議の解明です。「なぜ奇数整数半径が出て来るのか？」について深掘りしてみましょう。

深掘：ボールの半径はなぜ奇数整数になるのか？

　話を統一的に考えるためボールの半径をr、ボールの下のy座標をbとします：

このボールの式は、

です。解説と同様に放物線と接するので、

を上式に代入してyについて整理すると、

このyが重解を持つ（放物線に2点で接する）事が今回の問題のポイントなので、判別式から、

rとbの式が出て来るので、これを整理しrの2次方程式としてrを求めると、

このようにボールの半径rをボール下のy座標bで表す事が出来ます。ただこの式だけ見ると右辺にルートがあり、半径rが整数になりそうな感じはちょっとしないですよね…。でも、ここから美麗な事が起こります(^-^)

　上の式をベースに今回の問題の手順を回してみましょう。まず最初のボールは放物線の底に接します。これをb1=0と表すことにします。このb1を上の式に放り込むと、

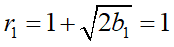
解説で求めたボール1の半径r1がちゃんと出てきました。

　次のボール2の半径r2は、このボールの底b2が、

なので、

ルートの中が上手い事べき乗になり整数解3が出てきました。おいおいマジかとr3も求めてみます。

やっぱり整数解になります！

　もっとそもそもな所にさらに踏み込みましょう。n個目のボールの半径rnは、

であり、n+1個目のボールの底の位置bn+1は

とそれぞれ漸化式で表されます。

　bn+1式の右辺のrnを置き換えると、

bのみの漸化式になります。ルートの中にbnがあるのがちょっと厄介なので、

と置き換えてルートから漸化式を追い出すと、

この右辺はよーく見るとべき乗式になっています：

両辺がべき乗なのでここから、

と2つの漸化式が導けます。プラス側は等差数列、マイナス側は等比数列になりますね。高校数学の漸化式の基本なので、導出過程を省いてパパっと解くとこうなります：

マイナス側は置いておいて(^-^;、プラス側の式をbnの式に戻します：

nは正の整数ですからこの右辺はすべて整数値です！ここからボールの底のy座標は常に整数である事がここからわかります。さらにこのbnをrnの式に戻します：

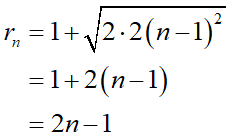
美しくルートが消え、半径が奇数整数になる式が導けました！

深掘2：マイナス側って何？

　上の漸化式を解く過程で出てきたマイナス側のCnって何なのか？これをBn及びrnに戻すと、

双方ともnが奇数番目の時と偶数番目の時でbは0と2、半径rは1と3を行ったり来たりする「振動」を起こしているのが分かりますね。これが意味する所について下図をご覧下さい：

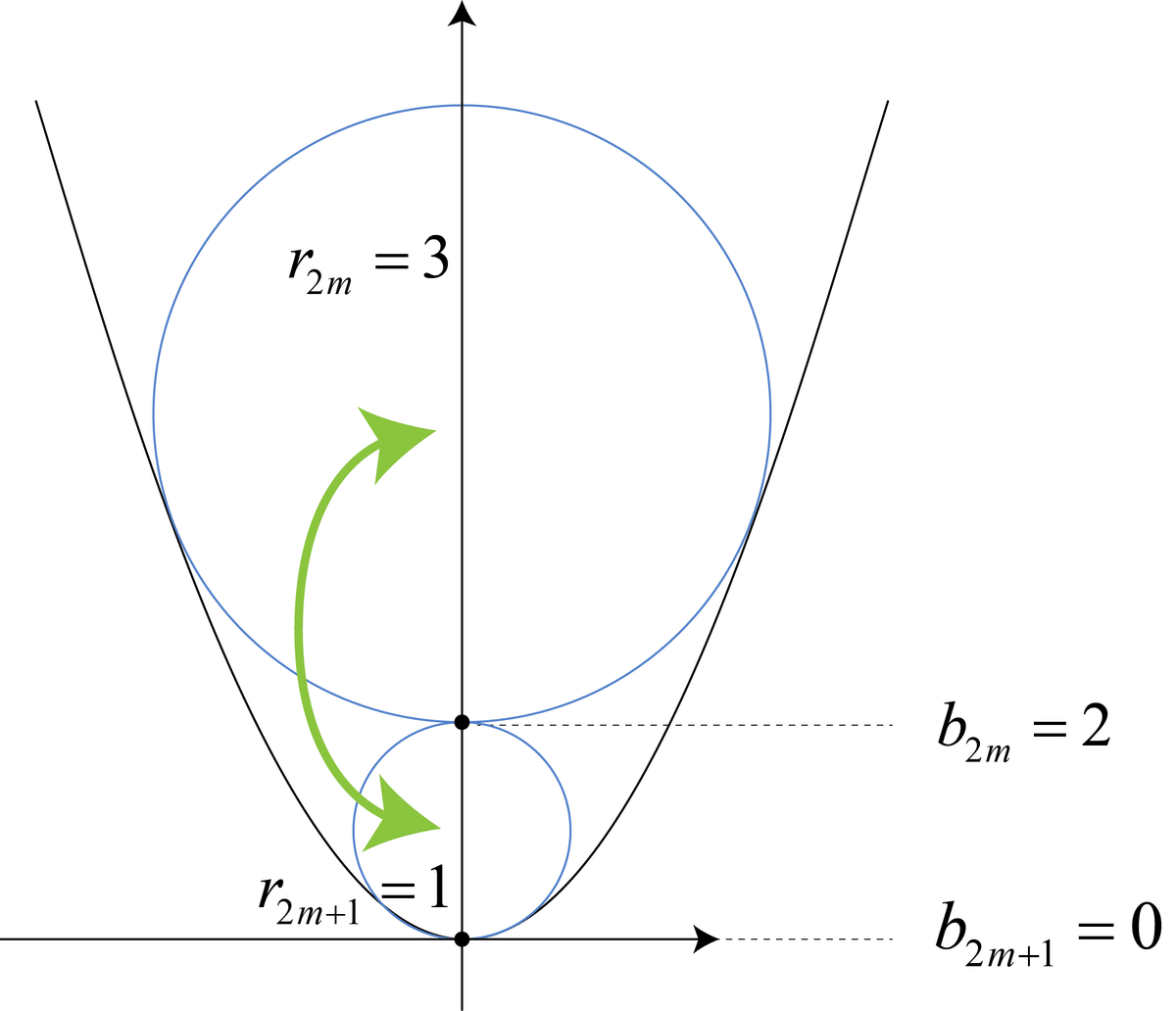
　n=1のボールは半径1で放物線に接します。次のn=2のボールは半径3。ここまではプラス側と一緒。次のn=3の条件は「ボール2に接して且つ放物線に接するボール」です。これ実は上側だけじゃなく下にあるn=1のボールもそれを満たすんですね。ここから奇数番目と偶数番目でボールが行ったり来たりするわけです。マイナス側の式はこれを示していたんですね。

　
　今回はボールの半径が美しく奇数整数になるのを順番に確かめて、その理由を式を展開する事で理解出来ました。式が如実に示す真実は強烈ですね。このように式が最後まで解けるのは有難い事です。そこから色々な現象や性質を読み解く事が出来ますから。でも世の中には解けない式も沢山あります。そういう解けない式からは何も分からないのでしょうか？これは必ずしもそういう訳ではありません。

　例えばちょっと極論的ですがsinθを解く式というのはありません（近似式はあります）。でも「sinθという物がそもそもある」としてしまえば、その範囲で解ける式がたくさん出来る事になります。それらの式はsinθの性質を何らかの形で反映しているので、sinθの性質を研究する事でそこからsinθを含む式が表す現象も読み解く事が出来るんです。

　解けない式のオンパレードと言うと積分を思い出す人も多いかと思います。これも実は同様で、f(x)の積分の解析的な式が無いとしても、答えとしてF(x)があるとしてしまえば、f(x)が含まれる式の積分の多くがF(x)で表された式として解けるようになるんです。この「f(x)の積分が解けないけどその答えをF(x)と定義してしまおう」という発想を活用している一分野が統計学です。例えば統計学で頻出する「正規分布の確率密度」も解析的に解けない積分です：

eの累乗なので解けそうな雰囲気もあるのですが…解けません。でもこれも「誤差関数」という積分式、

があるとしてしまう事で、

このように積分が無い（ように見える）形に解く事が出来ます。式内に誤差関数erf(x)があるので、正規分布の確率密度も誤差関数の性質を持ち合わせている事がわかります。解けない式からでも多くの情報を得られるんです。

　それにしても今回の問題、問題の条件で放物線にはまるボールの半径がうまく整数になるというのはホント神秘的ですよね。そういう神秘的な数学があればまたご紹介したいなと思います。ではまた(^-^)/