感染症のSIRモデル解説
感染症が発生し、どのように流行して終息するのかを数理モデルで表したものがSIRモデルです。今回はSIRモデルを解説します。知識ゼロの読者対象に分かりやすさ重視です。(高校数学の理解を前提としています)
S, I, Rとは?
S : Susceptible
未感染者(今後感染を受ける危険あり)
I : Infectious
自身が感染(他者に移す危険あり)
R : Recovered
既感染者(感染のリスクなし)
※今回は簡単のため死亡者の割合を考慮しません。
SIRモデルは上記の頭文字を取っています。
これらの頭文字を、総人口に対する比率として用い、感染の推移を数式で表していきます。
感染の様子 : S→I→R
総人口は不変 : S+I+R = 1
SIRモデルの基本となる3つの式
SIRモデルの理解の初めに、S→Iに関して感染が起きる条件を考えてみます。
1.2人が感染可能距離にいる
2.S集団とI集団が一人ずつ
3.ウイルスが転移する
感染は上記3つの条件が重なることで発生します。今回は特に2の条件を追っていきます。
「たまたま居合わせた2人がS集団とI集団の組み合わせになる確率」は積 SI に比例すると考えることができます。これを基に、S集団の変化率に関して以下の式が成立します。

S集団の割合の減少の度合い(感染者の増加具合)は積SIに比例し、比例定数を β>0 と置きます。この比例定数 β は感染が起きる条件1と3を反映します。つまり β は人同士の距離とウイルスの転移率によって決まる値です。
次にI→Rを考えていきます。I集団の中から一定の割合で回復者が生じると仮定すると以下の式が成立します。

R集団の割合の増加の度合い(感染者の減少具合)はIに比例し、比例定数を γ>0 と置きます。γは回復率と考えることができます。
最後にI集団を左辺におく式を立ててみます。①の式の右辺から-を除いたものはI集団の増加を表し、②の式の右辺に-をつけたものはI集団の減少を表すため、以下の式が成立します。

感染者の変化率がS,Iで表現されています。上記の式3つをまとめて以下に表示します。

③式を解く
③式はSとIの情報を含む微分方程式です。また、Rは全体からの引き算で求まるため、③式を中心に感染の様子を紐解いていくことができます。
初期段階においては、S≒1, I≒0と近似できるため、③式は以下のように書けます。

このように書くと、β>γ すなわり β/γ > 1のとき、感染者が拡大するきっかけになることが分かります。
今度はより厳密に見ていきます。③式を以下のように解いていきます。(一部大学数学の範囲含みます)

④式はある時点における感染者の割合を表しています。この式において重要な情報が2つあります。
1.感染者の数は時間に対して指数関数的に増減する
2.βS/γは基本再生産数(R)と呼ばれている
R は一人の感染者が何人の未感染者に感染させるかの期待値です。
β, S, γを整理してみます。
S : 未感染者の割合
β : I集団の人がだれかと出会い、ウイルスが転移する確率
1/γ : 感染してから回復までに要する時間 (γ: 回復率)
上記3つの積はつまり、「まさに今感染している人が、未感染者と出会い、ウイルスが転移する数」を表します。
Iを減らすにはβS/γを小さくし、βS/γ < 1 にする必要があります。考えてみれば当たり前ですが、人の行動や技術により上記パラメータを可変できる施策として、
γを大きくする = 回復を早くする = 薬や医療の充実(免疫力up)
βを小さくする = ソーシャルディスタンスを保つ、マスクをつける
これらが挙げられるわけです。
シミュミレーション
③式を離散的に考え、グラフによるシュミレーションを実行します。
適当にβ=1.5, γ=0.5を設定すると、以下のようになります。
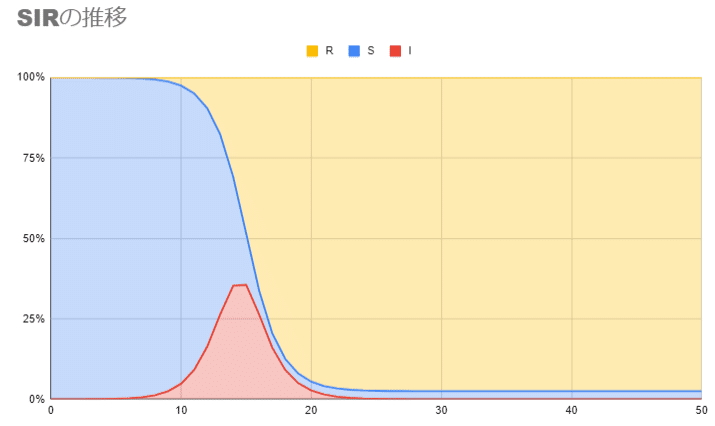
横軸は時間で、縦軸はS, I, Rそれぞれの割合です。大まかな特徴を言葉にすると、S, I, R比率に大きな変動があった後、それぞれ一定の割合に"収束"していきます。(後半Iが小さくなることを世間では終息と表現しています)感染症の推移は一般的にこれに近い経過をたどります。これを眺めてみると、以下3つのポイントが気になります。
1.Iの最大値(ピーク)はどれくらいか?
2.Iの最大値(ピーク)はいつか?
3.最終的なS, I, Rの割合はどのように決まるか?
ここでは1と3を解析的に紐解き、2をシュミレーションで紐解いていきます。(2を解析的に紐解くには高度な数学的技術が必要になります)
Iの最大値
やや突飛ですが、③式÷①式のように両辺同士割り算することを考えます。すると以下の式ができます。

今まではIを時間の関数として考えてきましたが、今度はSの関数として考えていきます。Iの最大値を考えるための道具としてSを利用するようなイメージです。これの両辺を積分することでIとSの直接の方程式を得ることができます。I, Sはそれぞれtの関数であり、IはSの関数でもあります。

⑤式でIとSの直接の関係を導くことができました。次に、Iの増減を調べるために、上記のIをSで微分したものを変形していきます。

右辺の符号はγ/βとSの大小関係で決まります。感染が拡大するきっかけとなる条件はβ/γ > 1 でした。今回は感染拡大後の話なので、0 < γ/β < 1が成り立ち、Sの変域内に存在します。ゆえにSI平面において、Iは上に凸な概形を描き、S = γ/βのときにIは最大値を取ることが分かります。これを⑤式に代入します。

上記の式を以下のように単純化します。x = γ/βと置きます。

これをxで微分します。

0 <x <1 のため導関数が負であり、M(x)は減少関数となります。
つまり、M(x)はγ/βが大きくなると減少していきます。さらにかみ砕いていうと、Iのピークはγ/βを大きくすると抑えられるということです。
収束した先のS, I, Rの割合
S, I, Rの割合は最終的に"収束"していく様子がグラフから分かります。またIは"終息"していくので最終状態(極限値)は、I=0を想定することができます。つまり、SとRの割合、ましてやSの割合のみで考えれば良いわけです。⑤式にI=0を代入すると、以下のようになります。 ここで用いるSは最終状態のときの割合です。

簡単のためx = γ/βと置いています。上記の方程式は一次関数と対数関数の組み合わせなので、値を求めることはできません。しかし、xに対して増加減少なのかを調べる術はあります。上記式の場合、xが決まればSも一つに決まるためSはxの関数です。そこで上記式をxで微分します。

⑥式は最終状態の S の変化率を表し、右辺の符号が分かればxに対する増減が分かります。
分子 : 0 < S < 1より分子 < 0
分母 : x = γ/β であり⑤の議論よりγ/βはmaxIのときのSの値。SI平面は上に凸な関数を描き、Sは1から減少する方向に動くため最終的なSの値はγ/βより小さいところに存在する。よって S< x なので分母 < 0
分子分母両方とも負なので、Sの変化率は正です。つまり、最終状態のSはγ/βが大きくなると増加していきます。かみ砕いていうと、最終状態のSはγ/βを大きくすると大きい割合で収束できるといことです。
γ/βを変えてシミュレーション
γ/βを変えてシミュレーションした結果が以下です。

シミュレーションから、上記2つの検討が正しいことが確認出来ています。また、γ/βが大きくなるとピークのタイミングが遅れることが分かります。ちなみに、γ/βが小さいときRの割合が大きくなり早く収束に向かいます。これが集団免疫で感染症をシャットアウトする考え方の基になる場合もあります。
まとめ
γ/βを大きくすると、良いことがたくさんあるということが分かりました。また、シミュレーションからもそれが正しいことが確認できました。
γ/βを大きくすると、
1.感染者のピークを小さくできる
2.未感染者の割合が大きいまま、収束(終息)を迎えられる
3.ピークのタイミングを遅らせることができる
以上のようなメリットがあります。1は医療崩壊を未然に防ぐことにつながります。2は最終的な死亡者数の抑制につながります。3は薬やワクチン、医療体制の整備の時間を取ることにつながります。
γ/βを大きくするために、、、
①βを減らす
βは感染が起きる3つの条件の1と3を反映しています。
1.2人が感染可能距離にいる
2.S集団とI集団が一人ずつ
3.ウイルスが転移する
つまり、βを減らすには
ソーシャルディスタンスを保ち、感染可能距離に入らない。
マスクをつけることでウイルスの転移可能性を小さくする。
上記のような行動をとる必要があります。
②γを増やす
γは感染者の回復率を表します。γを増やすには
薬の開発や医療の充実
免疫力up
これらが大事になってきます。
SIRモデルを紐解いていくと、現在声高に叫ばれている種々の措置の背景と効果を理解することができました。現状の日々の生活に意味付けすることで、より正しく、かつ納得して感染症と向き合うことができるかと思います。
この記事が気に入ったらサポートをしてみませんか?
