TCGのためのゆるい統計学 5-0したって、それ意味あるの?
「リーグで5-0した」
仲間との調整中よく見る報告である。
Magic Onlineでは5ラウンドのリーグというイベントが常設されているらしく、5回という丁度スコアリングに使いやすいラウンド数をしている。
レストランでも5つ星とかあるし、もっとでかい奇数よりも5というのはしっくりくる。例えば「31戦やって23勝」と言われるより、「リーグで4-1」と言われる方が印象に残りやすいししっくりくるのが人間のようである。前者のほうが断然信頼性が高いデータのはずなのだが。
私のチーム内での役割としては、
「5-0ゆうても5回じゃわからんくない?」
と盛り上がっているところに水を差す側に回ることが多いのだが、否定だけをしても不毛であるし、理由を説明せずに否定されると不快なだけ。
そういうわけで、
①少ないデータ数で出した勝率ってどんぐらい信用できないのか?
②じゃあどんだけデータを増やせば信用できるようになるのか?
③勝ち負け以上の建設的な議論とは何か
を一度まとめてみたくなったので記事を書く。
真の値と観測された値
なぜ戦績から勝率を出すのかというと、そのデッキの真の勝率が知りたいからだ。
真のってなんぞ?
例えば、70%勝てるデッキがあるとする。70%勝てるデッキなら強い。使いたい。
しかし、30%で負けるので、これが5回連続で起こって0-5する可能性もあるわけだ(0.2%ほど)。勝率0%のデッキは当然使いたくない。
この場合、勝率0%が観測された勝率で、70%が真の勝率というわけである。
すごく低い確率
では勝率70%のデッキで5回対戦すると何が起こるかを図にしてみる。

棒の高さが確率である。0-5から5-0の事象がこれぐらいの確率で起きる。期待値としては3.5勝ぐらいで、4-1が35%程度と最も高い頻度で現れるので感覚的にしっくりくるだろう。

一方で棒が潰れてほとんど見えないが、0-5の事象も起こりえる。確率は上にも書いた0.2%。
だが、これを見て
「ほら0-5することもあるじゃん!信用ならん!!」
とはならないはずだ。
大抵、
「すごい低いから無視しようぜ」
となるはずである。
人間、すごく低い確率については無視するものである。
今日も私は普通に外に出て歩道を歩いたが、もしかしたら老人の運転している車が突然突っ込んできて死ぬかもしれない。
だがいつも車が突然突っ込んでくることを考えながら歩道を歩いている人は滅多にいない。それが起こることが極めて稀であるからだ。
とはいえだ。0.2%は切り捨てるにしても15%の事象はどうか?
確かに15%はあまり高くない数字だが、15%で悪いことが起こるとするとかなり嫌だ。
15%で嘘をつく人と真面目な話をしようとは思わないし、15%で車が突っ込んでくると思っていたら絶対に外出しない。
70%のデッキで5回対戦する話に戻ると、じゃあ1-4する確率や2-3する確率はどうなんだという話である。
「0-5したから70%の勝率のデッキであることはまずないね!」
なんて議論がしたい場合もなくはない。
しかし、実際強いか半信半疑でやってみてどうという場合が大半。

図の赤で囲った部分、0-5から2-3の確率を足し合わせてみると16.3%である。まあ結構起こるなという印象の数字。
勝率70%のデッキでも16.3%で負け越す。逆に勝率30%のデッキでも16.3%で勝ち越す。
私がリーグ一回の戦績程度じゃなんもわからんと思っている感覚が伝わっただろうか?
たくさん対戦してみる
5回じゃ少ないからもっと対戦してみよう!というのが自然な発想。
では試しに勝率70%のデッキで100回対戦した場合の棒グラフを作ってみる。
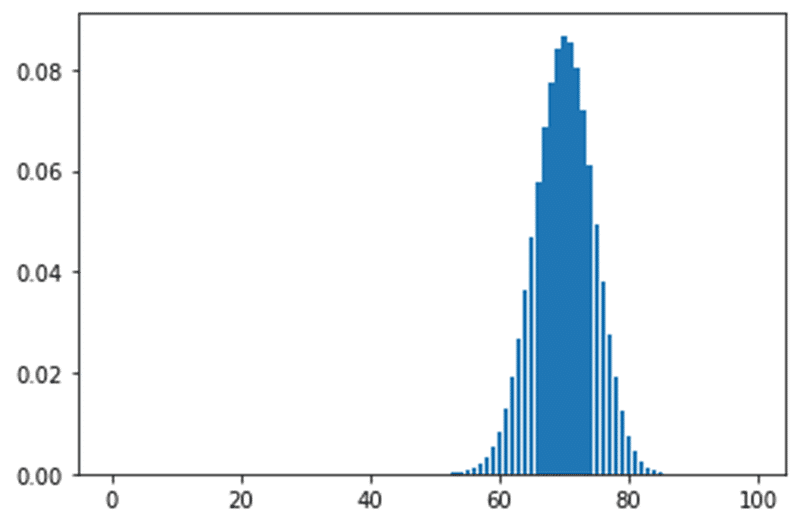
こんな感じ。

負け越す確率、つまり0-100から49-51の確率が赤枠の範囲。
もう見えん。ほとんど見えんとかじゃなくて完全に見えん。
数字にして合計0.02%。こんな確率普通考えない。
どこまで信用できる?
とはいえだ。デッキの勝率が50%より高いことがわかったところでじゃあ使おうとはならない。平均よりちょっと高いだけじゃあ魅力がない。
じゃあもうちょっと上を見て
「70%のデッキを100回回して60%以下しか勝てないなんてことがあるのか?」
と考えてみる。

対戦により60%以下の勝率が出る確率がこの範囲。
見える棒が範囲に入ってきている。数字にして合計2%。
2%か。まだ無視できるか。
さらに65%以下の領域だと12%という具合に、だんだんこれは無視したらよくないなあという数字になってくる。
一貫した議論をするためには
「これ以下の確率ならないと思うことにしよう!」
という基準を決めることになる(有意水準)。
大抵この水準は0.05に設定される。これはつまり95%以上のことであれば、偶然ではない意味のあることだと思うようにしようということ。
確率分布
一旦ここで、「〇〇から〇〇の値の事象がそれぞれ××の確率で起きる」という分布を一般化したい。
今まで使っていた棒グラフは棒が対応している点の事柄しか表すことができない。だが実際は40%と60%には50%があるし、その間には45%もあり、その間、間を考えると連続してずっと値がある。
「勝ち-負け」の二つの事象が試行回数の数だけ出る分布は正規分布というものに近似できる。
これは平均に近い値が出やすく、平均からはなれるにつれてその値が出にくくなるという性質の分布だ。(式をちゃんと勉強したい人はWikipediaでもどうぞ。)
例えば平均が70、分散21の正規分布はこんな感じ。

上の勝率70%のデッキで100回対戦するときの結果の分布と似たような形をしているのがわかるだろう。
数字と数字の間に値のない棒グラフ(50と51の間に50.5はない)と違って、滑らかな線なので0~100の間のどこにも対応する値がある。50.5に対応する値もあれば、50.25に対応する値もあるし、循環小数55.555…やその他任意の0~100の範囲にある無限通りの数に対応する値がある。
観測された勝率ではなく、真の勝率を考えるには連続したものを考える必要がある。
100回対戦したうちの勝った数を勝率(%)とするのであれば、55%の一つ上の勝率は56%。しかし、真の勝率が55%よりちょっと強いデッキはというと、55.5%かもしれないし、55.1%かもしれない。なので連続して値がある必要がある。
ではこれをどう使うかというと、
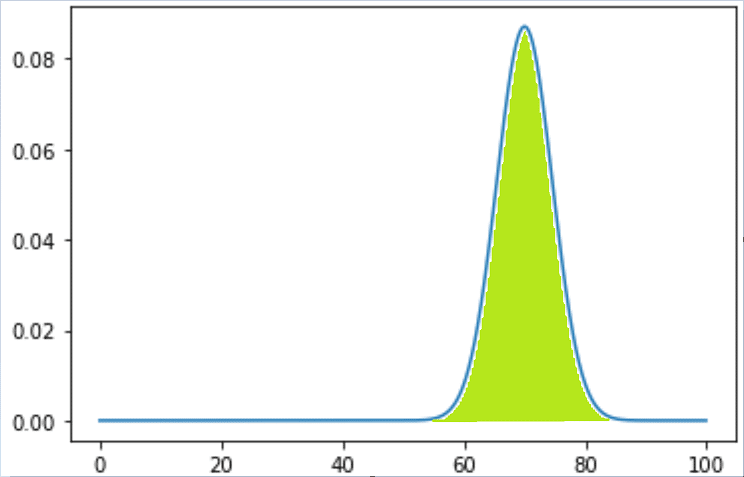
まずこの緑の面積が1になるようにできている。
ここにある分布から0~100までの数字がランダムに出てくるとすると、それが60~80の間にある確率はいくらか?と知りたいとき、

そこに60から80の部分の赤い面積が0.8(計算してない、適当)だとすると、その確率は0.8、つまり80%だということである。
確率密度関数を使うと何ができるかというと、観測された勝率から真の勝率の分布を出すことができる。
例えば5-5したデッキについて、多分これは50%ぐらいで勝つデッキだ。だが55%や45%ぐらいの可能性も高い。すごく低い確率だが5%や95%というのもありえなくはない。
みたいなことを具体的に表すことができる。
信頼区間
これを使えば、対戦による戦績からそのデッキの勝率、例えば
「50%の対戦による勝率のデッキの真の勝率は60%で40%から60%の間にあります」
というようなことが言えるようになる。

50%の±10%の区間より、例えば±20%の区間に入る面積のほうが大きい。
(図を作りやすかったので正規分布を使っているが深い意味はない。)

こんな感じで、95%信頼できる情報が欲しい!となったときにこの区間を広げていって面積が0.95になるようにすればいい。
逆に言えば赤まるのとこの面積の和が0.05以下になるようにすればいい。

こんな感じのがお世話になっている人も多いであろうmtgmetaの勝率マトリクスにも載っている数字。

この[41.2%-69.1%]ってなんぞやというと、信頼区間なのだ。これは95%で信頼できるWilsonの信頼区間である。
Wilsonの信頼区間がなんぞやという話は長くなりそうで数字が沢山出てくるので一番下の付録で。
信頼区間の大きさ
信頼区間の幅は何を意味しているか?
データ数が増えると確率的な広がりが狭まる。

青い分布では40以下や60以上の領域にも分布があるが、オレンジのようなデータ数の多い(分散の小さい)分布では、40~60でほとんどの区間をカバーできる。このようにデータを増やすと真の値に向かって確率が閉じていくイメージ。
ざっくりここまでのまとめ
低い確率でもゼロでなければ起こることはあるぞ
でも全部考えると何も話ができないからある程度起こりづらいことは考えないようにしよう(例えば5%未満でしか起こらないことは考えないようにしよう)
そうすると、対戦結果からこのデッキの勝率は〇%から〇%ぐらいだという感じの主張ができるぞ
対戦回数を増やすと、より正確な主張ができるぞ(例えば4-1したデッキの勝率は36~96%としか主張できなくても、400-100したデッキの勝率なら76~83%と主張できるぞ)
改めて、たくさん対戦してみる
では信頼区間の概念の導入をしたところで、改めて対戦数を増やしてデータの正確性を増すことを考える。冒頭の5回対戦する試行をベースに考察してみたい。
mtgmetaでも使われているWilsonの信頼区間を4-1やそれを何倍かした4-2、12-3について出してみる。計算にはscipyに入っているパッケージを使った。
まず4-1について…
38%-98%!
まあ一回ならこんなもんだろう。やっぱ一回程度じゃ信用ならん。
次に8-2したら
49-94%!
うーん、10回やったら結構信用できるかと思ったら、実は勝率50%以上であることすら示せていない。
じゃあ12-3したら
59-92%!
15回も回したら結構回した感じがするが、それでもまだ8割の勝率を出しているのにしては59%が下限とは悲しい話である…
いったいいつになったらこのデッキなら是非とも使いたいと思える区間にできるのだ…
まどろっこしいので一気にグラフにしてみる。

横軸が試行回数で縦軸が信頼区間の下限。8割勝っているという設定なので、横軸が100のところでは80-20しているということ。
とりあえず70%であるというのに十分な試行回数を見てみる。わかりやすいように0.7のところにオレンジで平行線を引いた。
オレンジの線と交わるのは。80回対戦したあたり!!
・・・あの、多すぎませんか?
本当の勝率が80%あるのに80回も対戦しないと70%の勝率があることすら示せないのか?
信頼度が高すぎたかもしれない。95%なくても90%あれば信頼できるということにしてみる。

少なくとも70%の勝率があることを示すのに必要な対戦回数・・・55回!!
・・・多すぎないか?
多すぎるよ。
少なくとも筆者が凄いデッキができたと思って回してみて、16-4したところで調整仲間に報告して
「いや、20戦?もう30戦やってや」
と言われたらキレる。
いやいや。勝率80%なんてあんまないので特例かもしれない。
もっとありそうな、
デッキの勝率が65%以上であることを示せる7-3あるいは7X-3Xの戦績はどれだけ対戦すれば出せるか
を計算してみる。

まず信頼度95%。
必要な対戦数、340。
無茶を言うな。

次に信頼度90%。
必要な対戦数、270。
ふざけるな。
データを見ることに意味はありません。
いかがでしたか?
・・・というわけではなく、もう少し続く。
データは役に立つのか?
TCGで何かを証明できるような量のあるデータはそうそうないし、作ることもとても難しいということがわかった。
だが、当たり前ではあるが、証明できなくても〇〇かもしれないという示唆を様々なデータが与えてくれることには間違いない。そしてそれがどれだけ信頼できるかを知っておくことには意義がある。
もし今まで信頼区間が何かをわからずに勝率マトリクスを見ていた人が本記事を見たのであれば少しはお役に立てたのではなかろうか。
では、個人として採取するデータに意味はあるのか?一人で取れるデータなんかたかがしれているし、チームを組んだとしても特定のデッキ2つのマッチングあたりのデータ量なんかたかがしれているのではないか?
対戦結果の持つ広がり
チーム調整をしているプレイヤーがよい戦績を出すことは私も経験している。チーム調整の真の価値とはデータ数ではなくデータの質であるということだ。
勝ちor負けはたくさんのデータを二つの値になるまでそぎ落としてしまっている。どのように勝ったのか、あるいは負けたのか。
他のゲームで考えてみると、囲碁は得点があるのでどれだけの差でゲームが終わったかわかる。将棋は何手差という形で差が出る。
マジックでもそうであるはずだ。負けた側はカードが何枚足りなかった、ライフが何点足りなかった、マナがいくつ足りなかったなどの過程がある。
特定の相手に有利か、同じ勝率でもデッキ相性やデッキのぶれのどちらが大きく影響しているかなど、戦績を見ただけではわからないたくさんの評価すべき要素がある。
戦績はそれらの情報の広がりをそぎ落とされてしまった情報だ。
チームのような密なコミュニケーションが取れるところで重視すべきは情報の質である。
以前書いたように、言語化もまた情報をそぎ落とす行為である。個人で取って人に伝えるとき質の良い情報とは、全ゲームログと戦績の間にある情報の中から有益なものを選んで抜き出したものだろう。
有利不利やデッキの強弱は勝敗以外の様々な要素から語ることができる。
すごく月並みな話で恐縮だが、ツールは有効な範囲で正しく使うべきだ。範囲外では別のツールを使おう。
そしてあるツールができないことを知っていれば他のツールをより有効に役立てることもできる。玉石混交の多数のプレイヤーの勝敗という統計からわかること、わからないことを頭に入れておけば日々の練習でより有益な知見を得られるだろう。
参考文献
[1]Wilson, Edwin B. “Probable Inference, the Law of Succession, and Statistical Inference.” Journal of the American Statistical Association, vol. 22, no. 158, 1927, pp. 209–12. JSTOR
[2]mtgmeta
[3]Wikipedia Binomial proportion confidence interval
付録:Wilsonの信頼区間の概要と導出
Wilsonの信頼区間は非対称であることが特徴で、少ないデータ数のものに対しよい性質を持つとされる。
まず、成功数/試行数(ここでは勝数対戦数)を$${p_0}$$、求めたい確率を$${p}$$、試行回数をnとする。
ここで、$${p_0}$$と$${p}$$の差についてカイ値を計算する。有意水準を満たすように選んだ$${\lambda}$$に対し信頼区間の上限および下限の関係は次のようになる。
$$
(p-p_0)^2=\lambda^2p(1-p)/n
$$
有意水準0.05であれば$${\lambda\approx1.96}$$。
これを$${p}$$について解くことで信頼区間の上限と下限が得られる。
$${t=\lambda^2/n}$$と置くと次のようになる。
$$
p=\frac{p_0+t/2}{1+t} \pm\frac{\sqrt{p_0(1-p_0)t+t^2/4}}{1+t}
$$
これがウィルソンの信頼区間の上限と下限。
この信頼区間にどのような利点があるか、試行数と成功数から正規分布を用いて出した信頼区間と比較する。


それぞれ、ロジスティック曲線上を標本平均が動いたとき、n=10,100の場合について信頼区間の上限と下限を示している。
上の図の場合、平均が0あるいは1に近づいたとき2つの問題が起きている。
①信頼区間が存在しないはずの0未満、あるいは1を超えるところまではみ出ている
②0と1近傍で信頼区間がなくなっている(具体的には、全部成功、あるいは全部失敗の場合、100%の信頼度で必ず成功または失敗するという結果になってしまう。極端な話、n=1だと必ず成功するあるいは必ず失敗する試行であるという結果になってしまう。)
下の図を見るとこれらが解決しているのがわかるだろう。
コミュを始めました。面白かったからもっと書けという方は入っていただけるとやる気が出ます!よろしくお願い致します!
おもろいこと書くやんけ、ちょっと金投げたるわというあなたの気持ちが最大の報酬 今日という日に彩りをくれてありがとう
