
統計的な推測~とりあえず二項分布のおさらいまで
Cover Photo by Christopher Burns on Unsplash
数学B「統計的な推測」
統計的な推測について,数学的活動を通して,その有用性を認識するとともに次の事項を身に付けることができるよう指導する。
ア 知識・技能
(ア)標本調査の考え方について理解を深めること。
(イ)確率変数と確率分布について理解すること。
(ウ)二項分布と正規分布の性質や特徴について理解すること。
(エ)正規分布を用いた区間推定及び仮説検定の方法を理解すること。
イ 思考力,判断力,表現力等
(ア)確率分布や標本分布の特徴を,確率変数の平均,分散,標準偏差などを用いて考察すること。
(イ)目的に応じて標本調査を設計し,収集したデータを基にコンピュータなどの情報機器を用いて処理するなどして,母集団の特徴や傾向を推測し判断するとともに,標本調査の方法や結果を批判的に考察すること。
[用語・記号] 信頼区間,有意水準
数学Bでは「統計的な推測」を扱うことになっています。指導要領に示されている内容は上記の通りですが、これ、高校生がやるのですよ。本当か?と思ってしまいます。だって、「確率変数と確率分布」って、めちゃめちゃ抽象的な概念ですよ(書いている本人だって自信がない)。区間推定や仮説検定の方法を理解したら、とりあえず統計学はかなり一人前ですよ。
とはいえ、扱う確率変数や確率分布は、離散型、具体的には二項分布が中心ですし、Nが大きくなると二項分布が正規分布で近似できることを利用して、平均から標準偏差いくつ分離れているから、ということをもとに議論を進める、みたいなところが中心になっているようですけど。それにしたって、コンピュータがちゃんと使えないと計算できませんからね。ハードルはめちゃ高いと思います。
では、順にみていきますが、とりあえず「標本調査」は省略しましょう。中学校で学習したことの復習が中心です。
確率変数と確率分布
さて、確率変数とは何でしょう。「解説」では、「ここで取り扱う確率変数は,標本空間の各要素に対し一つの実数を対応させる写像のことである」と説明しています。難しい!
確率分布として後に出てくるのは、二項分布と正規分布だけで、正規分布の定義については扱わないと書いてあるので、二項分布に絞って考えましょう。問題を具体化します。「サイコロを5回振ったとき、1の目が何回出るか」を考えます。このとき、
「サイコロを5回振って、そのうち1の目が出た回数」が、確率変数ですね。6分の1の確率で成功(1の目)し、6分の5の確率で失敗(2~5の目)になる試行を5回繰り返していることになります。
この確率変数の取り得る値は、0~5の6種類しかありません。それぞれの場合の確率を表したものが確率分布ですね。「成功確率6分の1、試行回数5の二項分布」と表現できます。
たとえばこの確率変数が「1」という値をとる確率を考えましょう。5回のうち1回だけ成功し、残りの4回は失敗するということです。成功する確率は6分の1、失敗する確率は6分の5なので、これを掛け合わせればOKです。
単純にかけ合わせればOKなのは、例えば、1回目の試行と2回目の試行は独立であるからです。つまり、1回目に成功した(1の目)からといって、2回目に成功しやすく(または成功しにくく)なるとは考えられない、ということです。
次の式のようになります。
$$
\frac 16 \times \frac 56 \times \frac 56 \times \frac 56 \times \frac 56
$$
この式ではたまたま1回目に成功、その後は失敗、というパターンになっています。でも、成功するのが2回目だけ、3回目だけ、というパターンも考えなくてはいけません。したがって、
$$
\frac 56 \times \frac 16 \times \frac 56 \times \frac 56 \times \frac 56 (2回目だけ成功)\\
\frac 56 \times \frac 56 \times \frac 16 \times \frac 56 \times \frac 56 (3回目だけ成功) \\
\frac 56 \times \frac 56 \times \frac 56 \times \frac 16 \times \frac 56 (4回目だけ成功) \\
\frac 56 \times \frac 56 \times \frac 56 \times \frac 56 \times \frac 16 (5回目だけ成功)
$$
のようになります。わざわざ書きましたが、これらの式はすべて同じ答えですね。だって、掛け算する順番を変えただけですから。要は、「1回だけ成功するときのパターンは5種類あるから、後から"×5"をしないといけない」ことを理解しておけば良いのです。
では、「1回だけ成功するときのパターンは5種類」はどうやって求めればよいのかというと、5回のうち成功が1回になる組合せの数を、$$_5C_1$$ で計算すればよいのです。
ということで式を整理すると、次のようになります。
$$
_5C_1 \times (\frac16)^1 \times (\frac56)^4 = 0.4018…
$$
Excelの関数でこれを表すと、こうなります。実際には、成功が0回のときから5回のときまでまとめて計算できるように、セルの使い方を工夫し、それに合わせて式も工夫します。
=COMBIN(5, 1) * (1/6)^1 * (5/6)^4そうして計算したものをグラフにすると、確率分布のグラフが完成です。
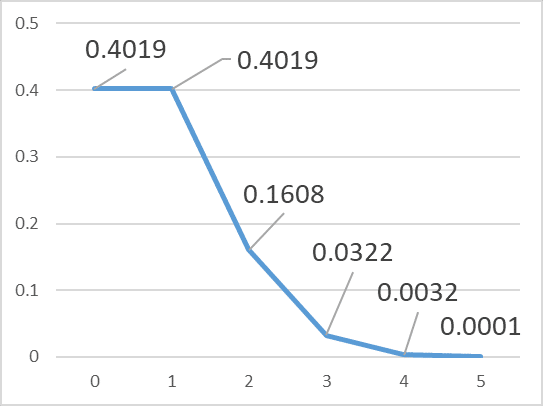
グラフからは、サイコロを5回振って1の目が出るのは、たいてい0回か1回で、3回以上出ることはほぼあり得ないことが分かりますね。
では、確率変数の定義に戻ります。「ここで取り扱う確率変数は,標本空間の各要素に対し一つの実数を対応させる写像のことである」というのが「解説」での定義でした。「標本空間の各要素」とは、ここでは確率変数がとりうるすべての値、すなわち0~6のことを言っています。それに、一つの実数を対応させるのです。確率変数の値が0のとき、確率は0.4019、1のとき0.4019、2のとき0.1608、、、のようにです。
これは別の言い方をすると、確率変数の値の決まり方にはルールがあるのだということを言っています。いま考えている確率変数は、0~6の値を取りますが、でたらめに値が決まるのではなく、0.4019の確率で0になり、0.4019の確率で1になり、0.1608の確率で2になり、というようにルールが決まっているというのです。この「値の決まり方にルール(確率)がある」というところが、通常の「変数」とは異なる、「確率変数」の特徴であると言えます。
二項分布の平均値(期待値)と分散
二項分布の平均値(期待値)と分散は以下の式で求められることがわかっています。
$$
E(X) = np, \ \ V(X)=np(1-p)
$$
ここで、nは試行回数、pは成功確率です。上の例にあてはめると、成功確率は6分の1でしたから、$${p=1/6}$$、サイコロを5回振っていましたから、$${n=5}$$です。よって、次のようになります。
$$
平均値 = np = 5 \times \frac16 = \frac56 \\分散 = np(1-p) = 5 \times \frac16 \times \frac56 =\frac{25}{36} \\ 標準偏差 = \sqrt{\frac{25}{36}}= \frac 56
$$
さて、二項分布の平均値や標準偏差について、グラフと関連づけて理解させる、と「解説」には書いてありますが、上のグラフでは少々無理があります。明らかに、正規分布(山型の分布)で近似できるようには見えないからです。したがって、もう少しnの大きい分布で考える必要があります。
もう、確率変数だけで2800文字も書いてしまっています。
質問です。これ、高校生は理解できるんでしょうか? もちろん、こういう問題にとても興味を持つ生徒や、とても得意な生徒はいることでしょう。しかしねえ、多くの生徒にとって、抽象的で、とてもとっつきにくい学習になりはしないかと。勝手に心配しています。(続く)
