
リソース関数
リソースというとビジネス風吹かしているみたいだけど、ここでは単に時間とか労力のことを指します。他に言葉が見つからなかったので、リソースという用語を使いました。
*
しがない物理学徒、コーシー分布と出会う
物理を勉強していたある日のこと。
コーシー分布(ローレンツ分布)というものに出会いました。
コーシー分布とは、以下のような関数です。
$$
f(x) = \frac{1}{\pi}\frac{\gamma}{(x-x_0)^2+\gamma^2}
$$
$${x_0}$$はコーシー分布の中心、$${\gamma}$$はコーシー分布の幅を意味しています(正式な名前があったと思いますが、忘れました)。
$${x_0=0}$$とし、$${\gamma}$$の値を変えてコーシー分布をグラフ化すると、
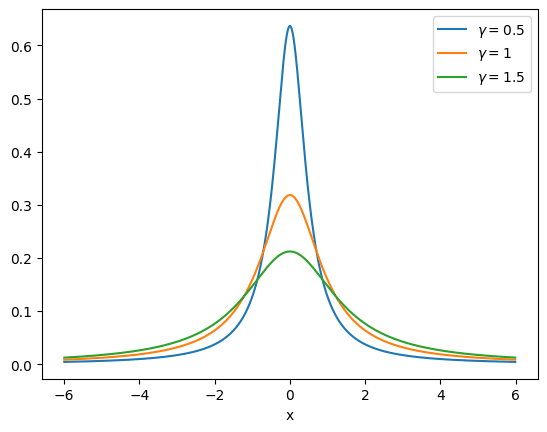
というようになります。
$${\gamma}$$を大きくすると、頂点の高さが低くなり、分布の裾(テールと言ったりもする)が広がっていくのが分かりますね。
逆に$${\gamma}$$を小さくすると、中心で鋭く尖り、裾の広がりが小さい分布になっていきます。
そしてコーシー分布は、$${x=-\infty}$$から$${x=\infty}$$までの全区間で積分すると、積分値が1になるという性質があります。
$${x_0}$$と$${\gamma}$$の値によらずです。
コーシー分布と日常生活
このコーシー分布を勉強した時、「これって、人が使えるリソースとなんか似ているな」と思いました。
どういうことなのかを、今から説明します。
$${x_0=0}$$すなわちコーシー分布の中心には、いま自分が最優先したいことだとします。
つまり、中心から離れていくほど、自分にとっては重要度は下がっていくものだと考えます。
そして縦軸の値は、費やせるリソースの量だとします。
時間やお金、精神的エネルギーなど、そういったもの。
グラフから見ても分かるように、中心から離れていくにしたがって、縦軸の値(すなわち、それに使えるリソース)が小さくなっていきます。
お山のような分布になっていたのを、思い出してください。
念の為にイラストも載せておきます。

さらにここから、コーシー分布の幅を表していた$${\gamma}$$を変化させて考えます。
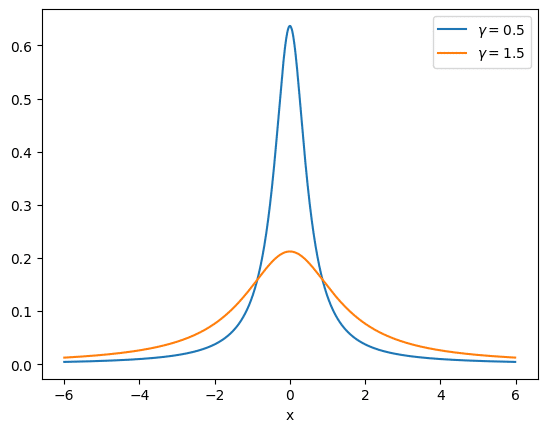
幅を大きくしていくと、優先度の低いものまで手を出せるようになるけど、中心の高さは低くなります。べちゃーっとした山みたいに。
色々なことをやっているけど、使える時間やエネルギーが分散されている状態。
反対に幅を小さくしていくと、中心やその付近の高さは高くなります。とんがりコーンみたいに。
やることを少なくしぼっているけど、それらに使える時間やエネルギーはしっかりある状態。
また、全区間で積分すると必ず1になるということも、自分が使える全リソースが決まっていることに対応づけられます。
コーシー分布の積分値が必ず1になり、$${\gamma}$$の値によらないことは、先ほど説明しました。
まとめ
以上をまとめると、人が使えるリソース量をコーシー分布に見立てたとき
幅を大きくする($${\gamma}$$を大きくすることに対応)と、色んなことに手を出せるが使えるがその分、それらに費やせるリソースは分散されて少なくなる
幅を小さくする($${\gamma}$$を小さくすることに対応)と、限られたことしかできないけど、その代わりにそれらに使えるリソース量は増える
使える全リソース量は1(コーシー分布の積分値が1であることに対応)としている
となります。
結局言いたかったことは、
人間が使えるリソースは限られているので、欲張ってたくさんのことをやろうとすると、どれも中途半端な結果に終わってしまう
という至極当たり前な結論なのでした。
それをグラフにすると面白いなって思っただけで、読者にはここまで付き合っていただきました。すみません。
自分には何が大事で、どのことに集中して取り組んだらいいのか分からない場合は、色んなことに手を出してみることは重要だと思います。
あと、多様なことをやっていると気分転換にもなりますしね。
また、経済学などでリスク管理の話になる際に、今回議論したコーシー分布は出てくるみたいなので気になった方はぜひ調べてみてください。
おまけ
コーシー分布で$${\gamma}$$を小さくすると、グラフが鋭く尖っていくことは説明しました。
では$${\gamma}$$を限りなく0に近づけると、どうなるのでしょうか。
例えば$${\gamma}$$=0.1、$${\gamma}$$=0.01と小さくしていくと、
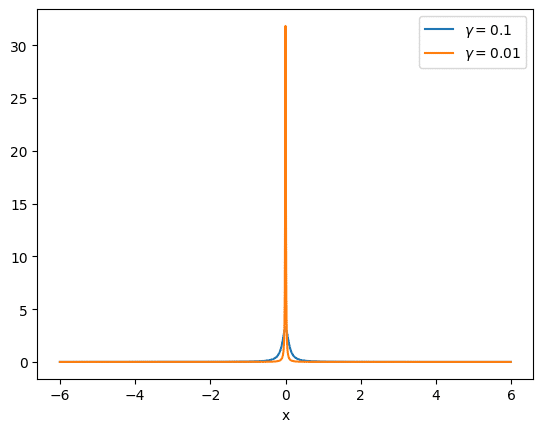
というように、幅がかなり狭くなって、中心近くの縦軸の値も大きくなっていきます。
さらにさらに$${\gamma}$$を小さくして、$${{\gamma}=10^{-8}}$$とすると、とんがりコーンの面影はもう無く、針金みたいになります。
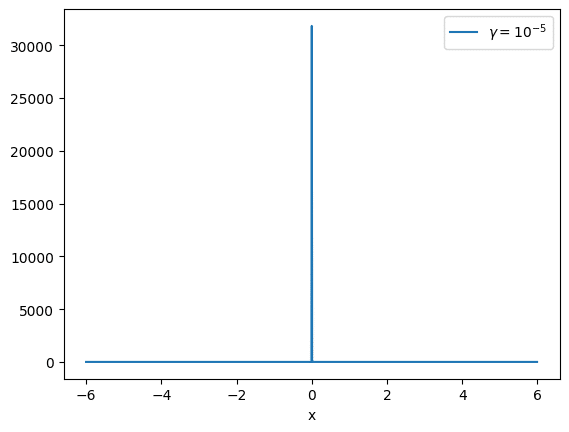
こうやって$${\gamma}$$を限りなく0に近づけると、コーシー分布はデルタ関数と呼ばれるものになります。
デルタ関数は
$$
\delta(x) = \left\{
\begin{array}{ll}
\infty & (x = 0)\\
0 & (x \neq0)
\end{array}
\right.
$$
$$
\int_{-\infty}^{\infty} \delta(x) dx = 1
$$
という性質があります。
グラフの中心では無限大になって、それ以外は0になるんですね。そして積分値は1になります。
リソースの話と関連させれば、一つのことだけに集中して一点突破した状態でしょうか。
そんなの、こわくてできない。
ちなみにデルタ関数は、物理学でよく出てきます。(数学や工学の分野でもそうなのかな?)
この記事が気に入ったらサポートをしてみませんか?
