2023年度下期・電験３種[理論]問１０　　コンデンサ充放電

問９はよくわからなかったので飛ばしました。いけそうなら解いてみます。

問１０は直流回路のコンデンサの充放電回路です。スイッチ入切したりする回路はまぁまぁ頻出な感じもしますが、コイルの時も合わせて苦手意識持ちやすそうなところですね。暗記だと間違えやすそうな問題です。

問題

解答群

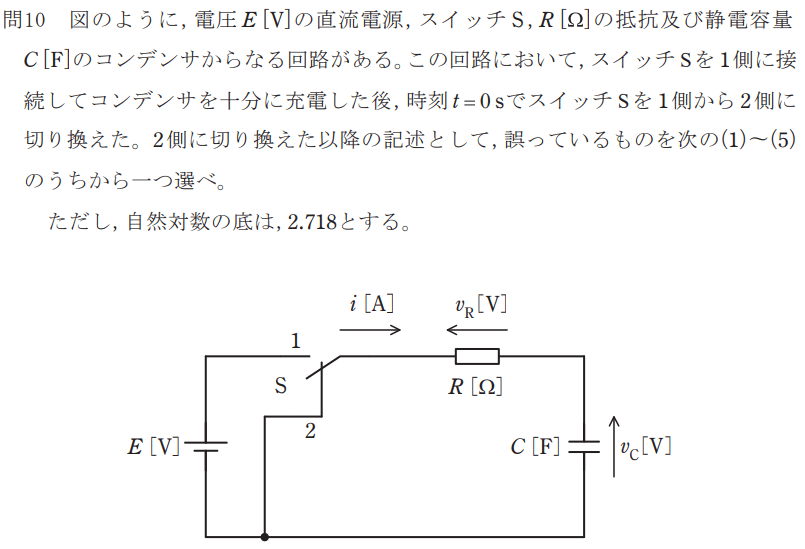
ちゃんと場合分けして進めましょう。
スイッチ１，２が時間で切り替わり、スイッチ１→２に切り替えた時刻が$${t=0}$$です。時刻によって、以下のように分けて回路は書けます。

$${t<0}$$の回路方程式を立ててみると、$${E=Ri(t)+\frac{1}{C} \int_{-\infty}^{t} idt}$$となります。
極値を考えると$${t \to -\infty}$$で$${v_c \to 0}$$、$${t \to -0}$$で$${i \to 0}$$となります。

以上を考慮して回路方程式を解くと、$${E=Ri(t) + \frac{1}{C} \int{i(t)}dt}$$をラプラス変換して、

$$
\begin{array}{}\frac{E}{s}&=&RI+ \frac{I}{Cs}\\
I&=&\frac{E}{s} \frac{1}{R+\frac{1}{Cs}}\\
&=&\frac{E/R}{s+1/(RC)}
\end{array}
$$

となります。ここからラプラス逆変換ですが、あんまり私も覚えてません。しかしながら、コンデンサ直列回路の電流は指数関数的に減少していくことが頭にあれば、なんとなく逆変換後の式の形がイメージできるのかなと思います。

$$
\begin{array}{}\mathcal L ^{-1}[I]&=&\mathcal L^{-1}[ \frac{E/R}{s+1/(RC)}]\\
&=&\frac{E}{R}\exp[-\frac{t}{RC}]\\
&=&\frac{E}{R}\exp[-\frac{t}{\tau}]\\
\end{array}
$$

時定数$${\tau}$$は、初期値の$${1/e=1/2.718=0.368}$$倍になる時間なので、$${t}$$の係数の逆数$${RC}$$が時定数となります。

時定数$${\tau}$$と$${t}$$って同じ式内に使われることが多いですけど、手書きだと見間違えそうで嫌なんですよね。。。

時定数を見ると直列回路の抵抗値、コンデンサ容量に比例します。すなわち、抵抗が大きいほど、またコンデンサ容量が大きくなるほど時定数が大きくなる＝電流の減衰が小さい、ということですね。

次に、$${t>0}$$の回路方程式を立ててみましょう。ただし、電流電圧は問題文に定義されているので、間違えないように気を付けましょう。
コンデンサの初期電荷がある状態ですが、下図のようにコンデンサを電池と見てあげた方がわかりやすいように思います。

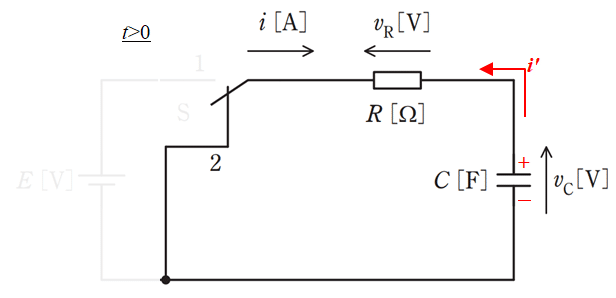
回路方程式は

$$
\begin{array}{}0&=&v_c+v_R\\
0&=&\frac{1}{C} \int_{0}^{t}idt+Ri\\
\end{array}
$$

極値を考えると$${t \to +0}$$で$${v_c \to E、i \to -E/R}$$、$${t \to +\infty }$$で$${i \to 0}$$となります。回路方程式をラプラス変換すると、

$$
\begin{array}{}0&=&\frac{1}{Cs}I+\frac{E}{s}+RI\\
I&=&-\frac{E}{s} \frac{1}{R+1/(Cs)}\\
&=&-\frac{E}{R} \frac{1}{s+1/(RC)}\\
\end{array}
$$

より、逆ラプラス変換して、$${i(t)=-\frac{E}{R}\exp{-\frac{t}{RC}}}$$となります。概ね、以下のようにグラフが書けると思います。

ということで、誤りは（５）ですね。

問題を適当に解いているだけなので、いろいろおかしくなっている部分があったらすみません。。。

出展：令和5年度下期　第三種電気主任技術者試験理論科目