中学生でも解ける！ピザの定理を証明しよう

今日は、ピザの定理と呼ばれる数学の定理をご紹介します。

この定理は1968年に海外の数学雑誌のチャレンジ問題として出題されました。その後、さまざまな証明方法が試みられています。

今回は、中学生でも理解できる方法でピザの定理を証明してみます。

ピザの定理の説明

ピザの定理とはいったいどんな定理なのでしょうか？

ここに1枚の円いピザがあるとします。これをピザカッターで8つのピースに切り分けて、二人で分け合うことにしましょう。

ピザの中心点が分かっていれば、その点を通るようにピザを切っていけばいいので簡単です。

では、中心点が分からないときはどうでしょうか？

実は、このような状況でも二人で分け合うことが可能だということをピザの定理は教えてくれるのです。

ただし、勝手気ままに切り分けてもうまくいきません。ある条件が必要です。

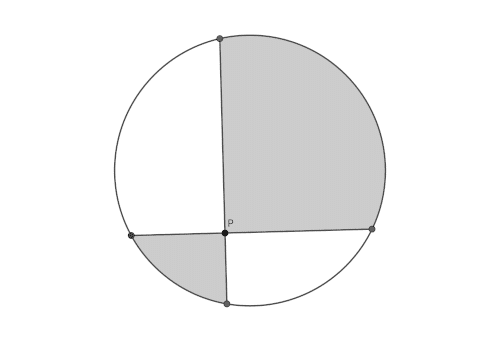
ピザ上に点Pを任意に取り（点Pは円の中心でなくてもかまいません）、点Pを通るように4本の直線を引いてピザを切り分けますが、このとき8つのピースの中心角がすべて45°になるようにしなければなりません。

下図をご覧ください。

この図を見る限り、8つのピースの面積はバラバラなように見えます。

ところが…

これらのピースを二人で交互に取り合うと、同じ面積になる！

というのが、ピザの定理の主張なのです（灰色の面積＝白色の面積）。

ピザの定理の証明

それではピザの定理を証明していくことにしましょう。

補助線として、点Pを通る同心円を引くのがコツです。

この補助円によって、ピザは2つのパーツに分かれます。

補助円の内部（これをAパーツと呼びましょう）。

そして、外側の円環部分（これをBパーツとします）。

証明の方針としては、それぞれのパーツにおいて「灰色の面積＝白色の面積」であることを示していきます。

Aパーツの証明

まずはAパーツから証明します。

4本の直線と補助円との交点は4つあるのでそれらを点I、点J、点K、点Lとします。このとき、四角形IJKLは実は正方形になります（下図を参照）。

この事実は「円周角の定理」から導かれます。例えば、辺IJにおいて、円周角IPJの角度は切り分け方から45°ですので、円の中心を点Oとすると中心角IOJは90°直角になります。残りの辺についても同様です。

あとは、三角形IPJと三角形KPLの面積の和が正方形IJKLの面積の半分になればよいのですが、これは直線IJと直線KLが平行であることから分かります（下図を参照）。

Bパーツの証明

続いてBパーツの証明です。

これには、以下のより強い形の補題を証明すれば十分です。

円環の内側の円周上に点Pと、点Pを通る2直線があり、2直線のなす角がθであるとします。このとき、この2直線によって切り取られる円環の部分の面積の和は、中心角2θのおうぎ形が切り取る円環の面積と等しくなります（下図を参照）。

補題の証明は、まず2直線のうち1本が中心Oを通る特殊な場合について考えます。この場合は下図から簡単に等しいことが分かります。

2直線がいずれも中心Oを通らないときは、中心Oを通る補助線を引くことで特殊な場合へと持ち込むことが出来ます。

以上で証明は終了です。

余談になりますが、この補題は点Pが円環の内部にある場合にも拡張することができます（下図を参照）。

ピザの定理の拡張

ピザの定理はピザを8つのピースに切り分けますが、それ以外の個数で切り分けるとどうなるのでしょうか？

4つのピースの場合

直角で４つのピースに切り分けてみましょう。

切り分けた直線のうち1本がたまたま中心を通ってくれたら等しく分けられます。

そうでない場合は、中心を含むピースがある方の面積の方が必ず大きくなります（下図を参照）。

4の倍数（12以降）の場合

ピースの数が4つならダメで、8つはOK。では12個ではどうでしょうか？

さらには16個、…、一般に4以外の4の倍数の場合は？

実は、この場合もピザの定理が成立します。証明もほとんど同じです（下図を参照）。

4の倍数以外の場合

ここまでくると、4の倍数以外の偶数の場合が気になります。

これについては、残念ながら中学生でもわかるような証明とはいきませんが、英語の論文を見つけることができました（以下のタイトルで検索すればPDFファイルを入手できると思います）。

"Of Cheese and Crust: A Proof of the Pizza Conjecture and Other Tasty Results"

興味のある人はぜひ、証明に挑戦してみてください。

今日はピザの定理の紹介と、その証明を行いました。