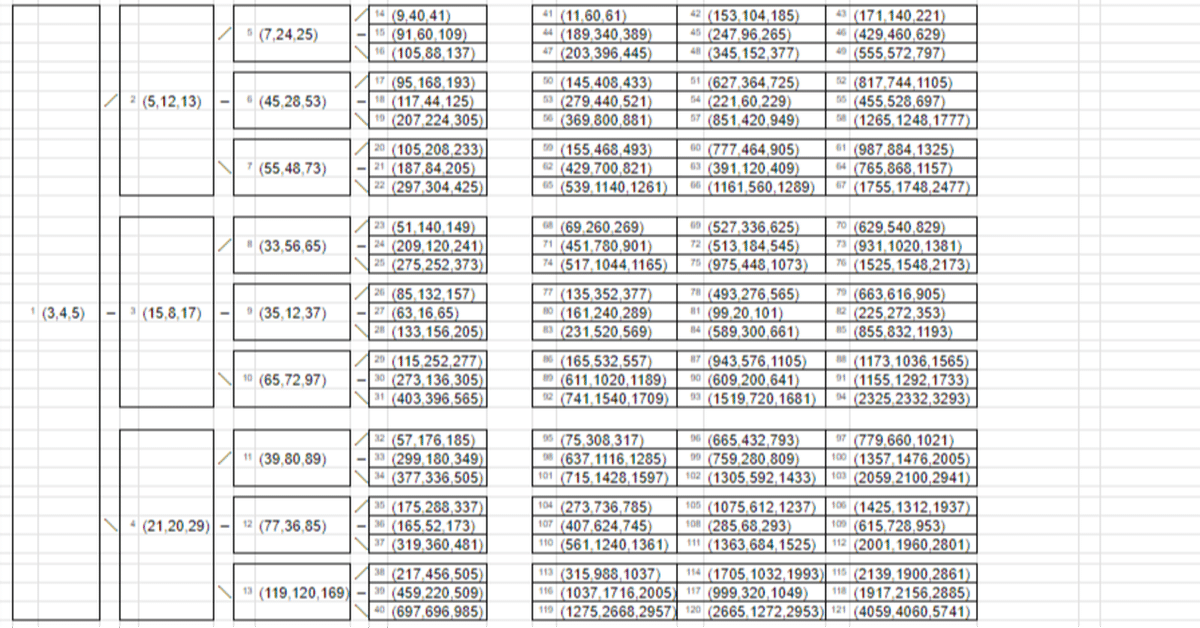
原始ピタゴラス数の整列 ~ ナンバリング
直角三角形にかかわる簡単な問題
問題です。
直角三角形があります。斜辺とある一辺の(長さの)差は3、斜辺ともう一辺の差は6です。三角形の三辺は何でしょうか?
解りましたか?
実はあることに気づけば秒殺できます。
3と6は両方とも3の倍数。
だから3で割った1と2で考え、最後に3倍にすればいいや。
直角三角形と言えば$${(3, 4, 5)}$$とかがあるけど、他には...
あれ!? これ、条件を満たしているじゃないか!
ということは、$${(9,12,15)}$$の三角形が答えだ。
同じような問題です。
直角三角形があります。斜辺とある一辺の(長さの)差は2、斜辺ともう一辺の差は8です。三角形の三辺は何でしょうか?
今度の問題は秒殺とはいきません。
さっきと同じように、最大公約数2で割ると、1と4。
直角三角形で、辺長の差が1と4なのは、... 思い浮かばない。
仕方ない、$${(c-2) ^2+(c-8) ^2=c^2}$$という方程式を
立てて整理。$${c^2-20c+68=0}$$→$${(c-10) ^2=32}$$
$${c=10\pm4\sqrt{2}}$$という解を得る。
斜辺を$${c=10-4\sqrt{2}}$$とした場合、$${c=2-4\sqrt{2}}$$という辺が現れてしまう。これは負なので不適。従って、複合はプラスの方だけ。
$${(2+4\sqrt{2},8+4\sqrt{2},10+4\sqrt{2})}$$ が答えだ!
最初の問題も、$${(c-3)^2+(c-6)^2=c^2}$$ という方程式を立て、
$${c^2-18c+45=0}$$→$${(c-3)(c-15)=0}$$から$${c=15}$$と答えに到ることができますが、このような問題を考えていた時、疑問が浮かびました。
・整数解に落ち着く場合とそうで無い場合があるが、何が違う?
・整数解になる条件は?
・それぞれ、負の辺長になるため除かれた解があるが、どう解釈できる?
この疑問が、全原始ピタゴラス数のナンバリングに繋がるアイデアの種になりました。
整数になる条件
まず、整数になる条件を考えてみましょう。問題はこうなります。
直角三角形があり、斜辺と他の二辺の差をそれぞれ$${p,q}$$とする。これらが整数の時、三辺が整数になる条件は?
直角三角形は斜辺が最も長い。その長さを$${z}$$とすると、この三角形は
$${(z-p,z-q,z)}$$を三辺とする直角三角形。ピタゴラスの定理より
$${(z-p)^2+(z-q)^2=z^2}$$
が成立。整理すると、$${z^2-2(p+q)z+p^2+q^2 = 0}$$となり、
$${z=p+q±\sqrt{(p+q)^2-(p^2+q^2) }=p+q±\sqrt{2pq}}$$
疑問の答えは明確になりました。$${2pq}$$が平方数であること。これが整数解になるための条件です。確かに、最初の問題では、$${2×3×6=6^2}$$ だし、次の問題では$${2×2×8=32}$$で、$${32}$$は平方数ではありません。
辺長が負?
三角形を前提に問題を考えていたので、辺長が負という状況が起こり、その解を棄てていました。しかし、少し一般化し、次のように問題を変えてみましょう。
$${x^2+y^2=z^2, z-x=p, z-y=q}$$
を解け。ただし、$${p, q}$$は正の定数。
実はすでに解けています。前項の結果がそのまま使え、
$${(x,y,z)=(q\pm\sqrt{2pq},p\pm\sqrt{2pq},p+q\pm\sqrt{2pq})}$$ (※)
が得られます。
$${\sqrt{2pq}}$$が気になりますが、実は、次のような関係があります。
$${2pq =2(z-x)(z-y)=2z^2-2(x+y)z+2xy}$$
$${ =z^2+(x^2+y^2)-2(x+y)z+2xy}$$
$${ =(x+y)^2-2(x+y)z+z^2=(x+y-z)^2}$$
$${\therefore \sqrt{2pq}=|x+y-z|}$$
途中でトリッキーな変形を行っています。$${2z^2}$$の一つの$${z^2}$$を$${x^2+y^2}$$に置き換えています。
$${\footnotesize(当時はこの変形がミソだと思っていました。しかしよく見てみると、このような変な}$$
$${\footnotesize 事をしなくても、(※)から直接この関係は引き出せることに気づき、脱力しました。)}$$
$${\sqrt{2pq}}$$が$${x,y,z}$$を使って簡単に表現できました。$${p,q}$$も$${x,y,z}$$と簡単な関係があります。ちょっと整理してみましょう。(※)を元の式に放り込むと、
$${(q\pm\sqrt{2pq}) ^2+(p\pm\sqrt{2pq}) ^2=(p+q\pm\sqrt{2pq}) ^2}$$
が得られます。この$${p,q,\sqrt{2pq}}$$を$${z-x,z-y,|x+y-z|}$$に戻すと、
$${\small {\{z-y\pm|x+y-z|\} ^2+\{z-x\pm|x+y-z|\} ^2=\{2z-x-y\pm|x+y-z|\} ^2}}$$
となります。この式は、
$${\small {\{z-y+(x+y-z)\} ^2+\{z-x+(x+y-z)\} ^2=\{2z-x-y+(x+y-z)\} ^2}}$$
または、
$${\small {\{z-y-(x+y-z)\} ^2+\{z-x-(x+y-z)\} ^2=\{2z-x-y-(x+y-z)\} ^2}}$$
を意味します。前者を整理すると、$${x^2+y^2=z^2}$$というスタート地点の式に戻るだけですが、後者からは、
$${(-x-2y+2z)^2+(-2x-y+2z)^2=(-2x-2y+3z)^2}$$
という、なにやら見慣れない式が現れます。果たして、正しい式なのかと疑問に思い、$${(-x-2y+2z)^2+(-2x-y+2z)^2-(-2x-2y+3z)^2}$$を計算すると、$${x^2+y^2-z^2}$$となります。なるほど、確かに、$${x^2+y^2=z^2}$$が成立するなら、成立する式であると確認できます。
恒等式
「$${x^2+y^2=z^2}$$が成立するなら、
$${(-x-2y+2z)^2+(-2x-y+2z)^2=(-2x-2y+3z)^2}$$が成立」
先ほどは、このように書きました。間違いではありませんが、成果の一面しか表していませんでした。
成果を正当に表現するのは次です。
$${(-x-2y+2z)^2+(-2x-y+2z)^2-(-2x-2y+3z)^2=x^2+y^2-z^2}$$
は、恒等式である。
注目すべきなのは、左辺も、右辺も、$${△^2 + ▽^2 -◇^2}$$という形になっていることです。従って、$${(a,b,c)}$$が$${x^2+y^2-z^2=k}$$の解ならば、
$${a_0=-a-2b+2c,b_0=-2a-b+2c,c_0=-2a-2b+3c}$$ (1)
で定まる$${(a_0,b_0,c_0)}$$ も$${x^2+y^2-z^2=k}$$の解です。
今まで、$${x^2+y^2=z^2}$$つまり、$${x^2+y^2-z^2=0}$$について考えてきましたが、右辺が$${0}$$である必要はありません。
$${x^2+y^2-z^2=0}$$を三次元空間の曲面と見なすと、円錐です。ピタゴラス数の研究は円錐上の格子点の研究といえますが、$${x^2+y^2-z^2=k}$$となると、一葉双曲面、あるいは、二葉双曲面で、これらの研究にもあの恒等式は利用できます。
さらに、$${(a,b,c)}$$が$${x^2+y^2-z^2=k}$$の解ならば、$${(±a,±b,±c)}$$(複合任意)も$${x^2+y^2-z^2=k}$$の解になることに注意すれば、$${(a,b,c)}$$という一つの解から、最大8つの解を導き出すことができます。
符号の違いだけという面白くない解を除いても、通常4つの新たな解を引き出すことができます。
一つ目は、上の(1)の$${(a_0,b_0,c_0)}$$です。見比べるために、再掲します。
$${a_0=-a-2b+2c,b_0=-2a-b+2c,c_0=-2a-2b+3c}$$ (1)
二つ目は、(1)の中の$${a}$$の符号だけを変えたもの
$${a_1=a-2b+2c,b_1=2a-b+2c,c_1=2a-2b+3c}$$ (2)
三つ目は、(1)の中の$${b}$$の符号だけを変えたもの
$${a_2=-a+2b+2c,b_2=-2a+b+2c,c_2=-2a+2b+3c}$$ (3)
四つ目は、(1)の中の$${a}$$と$${b}$$の符号を変えたもの
$${a_3=a+2b+2c,b_3=2a+b+2c,c_3=2a+2b+3c}$$ (4)
具体的な値を入れると、よりわかりやすいでしょう。$${k=0}$$の時、$${(x,y,z)=(3,4,5)}$$は、$${x^2+y^2-z^2=0}$$の解になっています。
$${(a,b,c)=(3,4,5)}$$とすると、
$${(a_0,b_0,c_0)=(-1,0,1),(a_1,b_1,c_1)=(5,12,13),}$$
$${(a_2,b_2,c_2)=(15,8,17),(a_3,b_3,c_3)=(21,20,29)}$$
ここで得られた$${(5,12,13)}$$を新たに、$${(a,b,c)}$$と見なせば、
$${(a_0,b_0,c_0)=(-3,4,5),(a_1,b_1,c_1)=(7,24,25),}$$
$${(a_2,b_2,c_2)=(45,28,53),(a_3,b_3,c_3)=(55,48,73)}$$
この操作を繰り返せば、無限にピタゴラス数を見つけ出すことができそうですが、どうしてこのような方法で新しいピタゴラス数が見つかるのでしょうか?
幾何的意味
$${x^2+y^2=z^2}$$を、空間図形と見なせば、z軸を中心軸とし、原点を頂点とする円錐です。平面$${y=0}$$で円錐を切断すると、$${z=\pm x}$$が現れます。この$${z=\pm x}$$をz軸を中心軸として回転させたものともいえます。
$${(a,b,c)}$$をこの円錐上の格子点としましょう。この点を通り、方向ベクトル$${(1,1,1)}$$の直線が、再びこの円錐と交わる点が$${(a_0,b_0,c_0)}$$です。$${(a_1,b_1,c_1)}$$は、$${(-a,b,c)}$$を通り、方向ベクトル$${(1,1,1)}$$の直線が再びこの円錐と交わる点であり、他の点も同様に捕らえることができます。yz平面、xz平面に関する対称変換と、$${(1,1,1)}$$方向からの射影の組み合わせで、新しい格子点を見つけ出すというのが、この方法の幾何的解釈です。
C と Excel で
ピタゴラス数から、別のピタゴラス数を作り出す式を発見しましたが、実際これらの式を使って、コンピュータでたくさん生成させてみましょう。
#include<stdio.h>
int main(){
int i,j,k,m[3000][3],a,b,c,s1,s2;
m[1][0]=3;m[1][1]=4;m[1][2]=5;
for(i=2;i<3000;i++){
j=(i+1)%3;k=(i+1)/3;
a=m[k][0];b=m[k][1];c=m[k][2];
if(j==0){s1=-1;s2=1;}else if(j==1){s1=1;s2=-1;}else{s1=-1;s2=-1;}
m[i][0]= - s1*a -2*s2*b + 2*c;
m[i][1]= -2*s1*a - s2*b + 2*c;
m[i][2]= -2*s1*a -2*s2*b + 3*c;
}
for(i=1;i<3000;i++){
printf("%d : %d,%d,%d\n",i,m[i][0],m[i][1],m[i][2]);
}
return 0;
}
この C のコードは某所にて、ピタゴラス数の生成方法などを紹介した時に書いたものです。codepad さんのサイトに上げたものなのですが、現在でも確認できるようなのでリンクを張っておきます。リンク先では、実行結果として、2700個弱のピタゴラス数が確認できます。
もう一つ Excelでの生成方法を上げておきます。
Excel上の A1~D1、および、A2~J2 の各セルに、下のコロン(:)以降を書き込み(ペーストし)、二行目を三行目以降にコピーしてください。するとA,B,C 列にピタゴラス数が生成されます。アルゴリズムは全く同一です。
A1:3
B1:4
C1:5
D1:1
A2:=I2*F2+2*J2*G2+2*H2
B2:=2*I2*F2+J2*G2+2*H2
C2:=2*I2*F2+2*J2*G2+3*H2
D2:=D1+1
E2:=int((D2+1)/3)
F2:=INDEX($A$1:$C$1000,$E2,1)
G2:=INDEX($A$1:$C$1000,$E2,2)
H2:=INDEX($A$1:$C$1000,$E2,3)
I2:=if(mod(D2,3)=0,-1,1)
J2:=if(mod(D2,3)=2,-1,1)上手くいくと、下のようになります。

番号 ⇔ 原始ピタゴラス数
本来なら、これらのプログラムの背後について説明を与えるべきですが、少し後回しにして、別の二つのプログラムを上げておきます。
番号を指定してそれに対応する原始ピタゴラス数を表示するものと、その逆、原始ピタゴラス数を与えると、それに対応する番号を表示するものです。こちらは短いので、実行結果も示しておきます。
#include<stdio.h>
int f(int i,int *p){
if(i==1){
p[0]=3;p[1]=4;p[2]=5;
}else{
int j,k,a,b,c,s1,s2,q[3];
j=(i+1)%3;k=(i+1)/3;
f(k,q);
a=q[0];b=q[1];c=q[2];
if(j==0){s1=-1;s2=1;}else if(j==1){s1=1;s2=-1;}else{s1=-1;s2=-1;}
p[0]= - s1*a -2*s2*b + 2*c;
p[1]= -2*s1*a - s2*b + 2*c;
p[2]= -2*s1*a -2*s2*b + 3*c;
}
return 0;
}
int main(){
int i,inputdata[10]={1,10,100,500,1000,2000,2500,10000,100000,1000000},p[3];
for(i=0;i<10;i++){
f(inputdata[i],p);
printf("%d : %d,%d,%d\n",inputdata[i],p[0],p[1],p[2]);
}
return 0;
}1 : 3,4,5
10 : 65,72,97
100 : 1357,1476,2005
500 : 693,2924,3005
1000 : 11505,13552,17777
2000 : 31457,68376,75265
2500 : 65221,56100,86029
10000 : 106329,119720,160121
100000 : 2101677,2246164,3076085
1000000 : 157186369,182904480,241167169#include<stdio.h>
int g(int *p){
if(p[2]<6){
if(p[0]==3 && p[1]==4)return 1;
else return 0;
}else{
int q[3],r;
q[0]=- p[0]-2*p[1]+2*p[2];
q[1]=-2*p[0]- p[1]+2*p[2];
q[2]=-2*p[0]-2*p[1]+3*p[2];
if(q[0]<0){
q[0]=-q[0];
if(q[1]<0){q[1]=-q[1];r=1;}else{r=-1;}
}else{
if(q[1]<0){q[1]=-q[1];r=0;}else{return 0;}
}
return 3*g(q)+r;
}
return 0;
}
int main(){
int inputdata[10][3]={{3,4,5},{65,72,97},{11505,13552,17777},{65221,56100,86029},{120927,107536,161825},
{57785,95448,111577},{55275,17612,58013},{106329,119720,160121},
{2101677,2246164,3076085},{157186369,182904480,241167169}},i,r,*p;
for(i=0;i<10;i++){
p=inputdata[i];
r=g(p);
printf("%d,%d,%d --> %d\n",p[0],p[1],p[2],r);
}
}3,4,5 --> 1
65,72,97 --> 10
11505,13552,17777 --> 1000
65221,56100,86029 --> 2500
120927,107536,161825 --> 9997
57785,95448,111577 --> 9998
55275,17612,58013 --> 9999
106329,119720,160121 --> 10000
2101677,2246164,3076085 --> 100000
157186369,182904480,241167169 --> 1000000補足。下のプログラム内の関数 g は、三つの数字(が入った配列のアドレス)を受けとりますが、その三つの数字が原始ピタゴラス数であること、しかもその順番は、奇数(小)、偶数、奇数(大)であることを前提に組んでいます。試す際はご注意下さい。
ここで番号?
恒等式の項では、ピタゴラス数から別のピタゴラス数を見つける式を示し、最後に「この操作を繰り返せば、無限にピタゴラス数を見つけ出すことができそうですが、...」と書きました。実行例を見て、確かにたくさんのピタゴラス数が生成されるのを確認されたのではないでしょうか。
最初のプログラム、あるいは、Excelの例では、たくさんのピタゴラス数が表示され、その隣には、1から順番に番号が振られています。一見すると、得られたピタゴラス数の「数」をカウントするため、何個目の出力なのか、それをただ表示しているだけのもののようにも見えます。
それも間違いではありませんが、正しくは、原始ピタゴラス数と番号がセットになっていて、それらを併記しています。下の二つのプログラムは、お互いに変換可能であることを示すために組んだものです。
「では、この番号はどのように決められているのか?」
ここからはこの疑問に対する説明を与えたいと思います。
$${a,b,c}$$を非負整数とします。$${(\pm a,\pm b,\pm c)}$$(複合任意)が(1)によって
$${(a',b',c')}$$に変換されたとき、$${(a,b,c)}$$と$${(|a'|,|b'|,|c'|)}$$をお互いに、「隣接」と呼ぶことにします。$${(a,b,c)}$$が、$${x^2+y^2=z^2}$$の解であれば、$${(\pm a,\pm b,\pm c)}$$等全てが解になりますが、とりあえず隣接という概念は、非負整数解同士間の概念としておきます。
すると、ピタゴラス数は、通常4つの隣接ピタゴラス数があるといえます。
隣接する原始ピタゴラス数同士を直線で結び、図示すると、とても興味深いものが見えてきます。ピタゴラス数と呼ぶべきか不明ですが、$${(1,0,1)}$$は、自分自身と隣接しており、伸びている直線は唯一$${(3,4,5)}$$だけ。$${(3,4,5)}$$からは他に三本の直線が伸びています。この三本は、$${(5,12,13),(15,8,17),(21,20,29)}$$へと繋がっており、それぞれが、また別の三本の直線を伸ばしている。このように、$${(1,0,1)}$$を除くと、完全三分木構造が見えてきます。
完全二分木構造と完全三分木構造
完全二分木構造の各ノードに、次のように順番に番号を与えてみます。
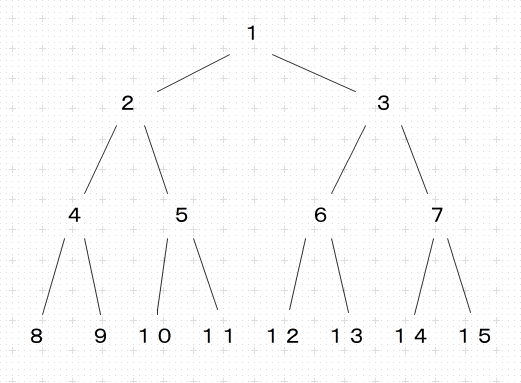
このように設定すると、親と子の番号の間には簡単な関係が見られます。
[〔子の番号〕÷2] が〔親の番号〕で、
〔親の番号〕×2,〔親の番号〕×2+1
等が〔子の番号〕です。似た関係が次のように番号を与えた完全三分木構造にも見られます。
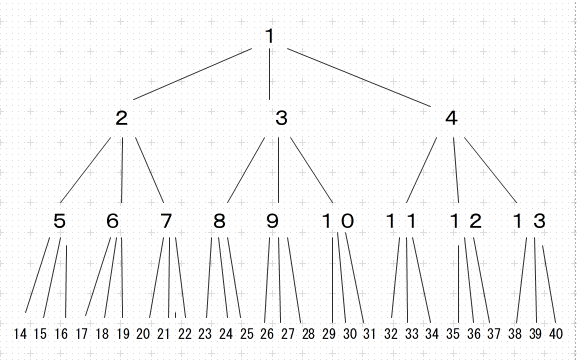
ご覧のように、[ (〔子の番号〕+1)÷3] で〔親の番号〕が解り、
〔親の番号〕×3-1,〔親の番号〕×3,〔親の番号〕×3+1
等が〔子の番号〕になります。
この番号を、同じく完全三分木構造をもつ原始ピタゴラス数に当てはめ、対応させたのが、これまで示してきたピタゴラス数の番号です。
ルール設定に向けて
$${a,b,c}$$を
$${a^2+b^2=c^2}$$、但し$${a,b,c}$$は 互いに素な非負整数 (★)
を満たすものとします。この時点で、$${c}$$が斜辺に対応することが決定しますが、$${aとb}$$についてはまだ入れ替えが可能です。大きさで指定する等の方法もあるのかもしれませんが、それは採用しませんでした。
(★)が満たされていれば、$${c}$$は奇数で、$${a,b}$$は、異なる偶奇を持ちます。そこで、$${a}$$を奇数側、$${b}$$を偶数側と指定することにしました。
すると、変換(1)~(4)では、これら$${a,b,c}$$の偶奇が常に維持されます。
これは大きな利点です。確認しやすいように、(1)を再掲しておきます。
$${a_0=-a-2b+2c,b_0=-2a-b+2c,c_0=-2a-2b+3c}$$ (1)
(★)を満たすものを、(2)~(4)によって変換し、
$${a_1,b_1,c_1,a_2,b_2,b_2,a_3,b_3,c_3}$$等を得ると、これらは全て正整数です。例えば、$${a_1=a-2b+2c}$$なので、$${b}$$が大きければ、負になることもあるのではと思うかもしれませんが、$${c}$$は斜辺なので、必ず$${ b < c }$$が成立し、$${a_1}$$は常に正となります。他も同様です。
他方、(★)を満たすものを、(1)によって変換し、$${a_0,b_0,c_0}$$を得ると、
次の三つのいずれかになります。
$${a_0<0,b_0≧0,c_0>0}$$ (2.1)
$${a_0>0,b_0≦0,c_0>0}$$ (3.1)
$${a_0<0,b_0≦0,c_0>0}$$ (4.1)
これらはそれぞれ、
$${(|a_0|,b_0,c_0)}$$に対し、変換(2)を行うと$${(a,b,c)}$$が得られる場合
$${(a_0,|b_0|,c_0)}$$に対し、変換(3)を行うと$${(a,b,c)}$$が得られる場合
$${(|a_0|,|b_0|,c_0)}$$に対し、変換(4)を行うと$${(a,b,c)}$$が得られる場合
に対応しています。変換(2)~(4)をどのようにして作ったのかを思い出すと、実は当たり前です。
つまり、変換(1)は、親となる隣接ピタゴラス数を見つけるだけで無く、$${a_0とb_0}$$の符号の組み合わせよって、(2),(3),(4)のいずれの変換によって、生成されたかという情報も与えてくれる変換なのです。
番号当てはめのルール
・(★)を満たすピタゴラス数において、$${a}$$は奇数、$${b}$$は偶数
・原始ピタゴラス数$${(3,4,5)}$$の番号を1とする
・変換(2)によって生成される子の番号は 〔親の番号〕×3-1
・変換(3)によって生成される子の番号は 〔親の番号〕×3
・変換(4)によって生成される子の番号は 〔親の番号〕×3+1
これらをルールとして設定し、コード化してます。
最後に
次回は、本件と関係が深い「ナゴヤ」等についての考察を記したいと思います。
また、原始ピタゴラス数のナンバリングについて考察していく中で、ここを細工すれば暗号の技術として成立するのではというアイデアが浮かびました。公開すべき鍵と秘密にすべき鍵をどのように組み合わせるか、利用する式にどれほどの自由度を設けるかなど、考えが纏まっていません。
もしかすると公開できるかも。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
