因数分解を学んだ僕たちが手にした圧倒的スキル
「学校の勉強なんて社会に出たら役に立たない」
今までに何度も言われてきた。今でも言われる。「そんなこと勉強して何になるの?」と。
僕は時間があれば勉強をする。政策学や社会学がメインだが、数学や物理学に興味が湧いてくることもある。別に研究者になろうって訳ではないし、アカデミックな才能がある訳でもないから、高度な事はよくわからない。あくまで大学1年とかでやるような教養科目くらいのレベル感だ。
確かに、意味などないのかもしれない。少なくとも、収入が増えたとか、モテるようになったとか、そういった形で確認できるメリットは今のところない。
不思議なことに、子どもの頃は「勉強しなさい」と言われるのに、そこそこいい歳になってくると「そんなの役に立たない」「頭でっかちになると社会で生きていけないぞ」「学力より人間力を高めろ」などと訳の分からないことを言われるようになる。(そもそも人間力ってなんだ?)
それでも僕は勉強を続ける。勉強という言葉が重く感じるのなら、学習でもいい。
わからないことを調べることは当たり前のことだし、何がわかっていないかをわかることも大切だ。毎日同じ仕事をしていると、「わからない」という感覚がなくなってくる。慣れによって、頭を使わなくてもできるようになっていく。折に触れてアカデミックなテーマに触れることは良い刺激になる。
それに、僕が好きな上司は皆、電車に乗っている時や休憩時間に勉強している。ニュースをみて、わからない言葉があれば調べる。僕が詳しそうなテーマであれば、部下である僕にも教えを乞う。それで気まずくなったりはしないから、人間関係には恵まれているのだと思う。
《アパレル店員に学歴はいらない。しかし・・・》
僕の仕事は服屋で服を売ること、いわゆるアパレル店員だ。
正直言って、学歴なんかいらない。東大で博士号を取ろうが、論文で賞を取ろうが、そんなことは関係ない。にっこりと挨拶できない人間は必要ないし、お客様が不快感を感じた時点で失格だ。
それこそ、理論ばかり勉強していて実際に接客をしたことがない「ノウハウコレクター」的な人はほぼ確実に嫌われる。だから、余分な知識を付けずにフィーリングで勝負した方がいいという意見もある。
ただし、学歴はいらないにしても、教養は必要だろうと強く思う。ニュースなどの時事的な話題からお客様との会話が弾むこともあるし、「貿易関係の仕事をしています」というお客様がいれば貿易関係の話で合わせるのが無難だろう。海外出張のあるお客様ならば、行き先の気候によってオススメするモノも変わってくる。自分に知識があれば、「そこって暑いんですか?」なんて無駄なヒアリングは省略できる。
専門家レベルまで鍛える必要はないし、そんなことは不可能なのだけど、大学1年の教養科目程度の知識を幅広い分野で持っていれば、多様な場面で対応できる大きな武器になる。
いや、中学レベルでも十分だ。多くの人は中学レベルの勉強も理解していないし、僕も理解できていない部分がある。クイズ番組とか、常識テストとかの問題も、中学レベルの教養があればそこそこ正解できる。(頭脳王みたいなのは無理だろうけど)
《義務教育レベルの知識も身に付いていない人》
アパレル店員に学歴はいらないと言ったが、義務教育レベルはこなせないといけない。
30%OFFの金額を出す時に0.7を掛けるが、「なんで0.7を掛けるんですか」と後輩に聞かれたことがある。
お客様対応に支障が出るといけないから教えるのだけど、正直言ってこのレベルの質問に答えるのは面倒臭い。一体学校で何を習ったのだろう。どうやって高校を卒業したのだろうと疑問である。
「寒冷前線通過したせいか急に寒くなったね」「なんですかそれ」
「この製法は19世紀のイギリスで・・・」「19世紀っていつですか」
こういう会話をしているとさすがに腹が立ってくる。義務教育で習うことというのは国民が共通認識として持っておくべきことだから、そこを疎かにすると会話にならない。
中学の勉強は中学生しかしてはいけないというきまりはないから、大人になっても中学の勉強をすればいいと思う。
《因数分解について。その前に因数について》
こんなことを偉そうに言っている僕だが、因数分解の話になった時にうまく説明できなかったことがある。
もちろん因数分解のやり方は知っているし、高校入試で出題されるような問題は一通り解けるのだけど、「因数分解とは何か」といった根本的で定義的な話となると、あまり考えたことがないなあと思う。
一応説明しておくが、因数分解とは、一つの整数あるいは整式(多項式)を、いくつかの整数あるいは整式の積の形に変形することである。要するに、式を掛け算の形にするということだ。
じゃあ因数ってなんだという話ではあるが、整式が、幾つかの整式の積の形で表されているとき、その各構成要素を因数という。
例えば12という数字は3×4と表現できるので、「3と4は12の因数である」というような言い方をする。(2と6でもいい)
12を3×4に分解する作業のことを因数分解という。
学校のテストとかで出るのはこういうことだ。
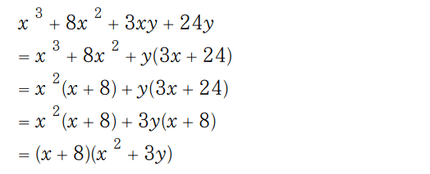
今これの解き方を解説することはしないが、複雑な多項式を積(掛け算)の形で表現することによって後の処理が楽になることがあるということは押さえていただきたい。
《服屋で働く僕が因数分解をする時》
因数分解について調べている時、「そういえば僕は毎日因数分解をしているなあ」と思い至った。
もちろん数学の入試問題を解いているという意味ではなく、もっと抽象的な話ではあるけれど。そして、これこそが今回のテーマだ。
自分の仕事において、自分の力で変えられることと変えられないことを考える時、そして何をどう変えていくかを考える時にこのような数学的思考になっていたと気が付いた。
ビジネスとして服を売る限り、利益を出さなければならない。売り上げからコストを引いたものが利益だから、
利益=売上ーコスト
と表現できる。商品の仕入れ代やテナントの家賃、人件費などが主なコストとして考えられるが、これらに関しては現場のスタッフが変えられる部分はとても小さい。
だから、自然と「どうやって売上を上げるか」という思考になる。多くの企業で売上目標があるのもこのためだと思う。
次に、どうすれば売上が上がるのかについてだが、ここで因数分解をする。
売上は客単価(一人のお客様が何円使うのか)と客数(何人のお客様が買い物するのか)の掛け算で考えるとわかりやすい。
売上=客単価×客数
「売上が伸びない・・・」となった時に、こうやって掛け算になおすことで、「一人当たりの使う金額が少ない」のか「お客様が少ないことが問題」なのかを明確にできる。
客単価を更に分解すると、一品単価と購入点数に分けられる。
客単価=一品単価×購入点数
このように分解することで「安物ばかり売れて高額な商品が売れていない」のか「まとめ買いしてもらえない」のかがわかる。
客数に関しても同じで、来店者数と購入割合に分けることができる。
購入客数=来店者数×購入割合
この数字を見れば、「そもそも人が来ていない」のか「来たけど何も買わずに帰ってしまう」のかがわかる。
これまでの話をまとめると以下のようになる。

このように分解すると大きなメリットがある。問題の所在を明らかにしやすいという点だ。
一品単価が低いのだとすれば、高額商品を売る努力をすべきだろう。それは、ディスプレイの変更かもしれないし、高額商品の魅力を伝える話術かもしれない。
購入割合が低いのだとしたら、店には来ているけど何も買わずに帰ってしまうお客様が多いということだから、何か気を引くような工夫が必要だろう。店員が不愛想で購買意欲をなくしてしまっているという可能性もある。
話が長くなるので省略するが、この調子で掛け算の要素に分解していけば、かなり具体的な問題に落とし込むことができる。何が課題なのかがわかれば後は改善をするかしないかという問題になる。
《多変数関数を整理するということ》
考えてみれば、服屋の売上を左右する要素は無数にある。商品の質、スタッフの能力、お店の立地といった企業側の抱える要素だけでなく、お客様の好み、地域性といったお客様側の都合や天候等の操作不可能な要素もある。
商品の質というのも曖昧で、デザイン、機能性、価格、生地や縫製のグレードなど様々である。
スタッフの能力というのも一概に言えるものではなく、話術に優れている人、細やかな気配りができる人、レジやパソコンなどの機械操作に強い人、目を引くポップ広告を作るのが上手い人など様々だ。自分の持っている能力やその時の状況によって、レジをスムーズにこなす練習をするべきか、他のスタッフとの協力関係を強くするべきかといった様々な手立てが可能性としてある。
大まかに考えて、「売上を上げよう!」と言われても、具体的に何をしたらいいのかわからない。
しかし、上記のように因数分解をしていくことで、問題を細かくしていくことができる。自分たちにとってネックとなっている点を明らかにすることで、それに特化した対策を練ることもできる。(何かに特化した結果、別の何かを犠牲にすることもあるので注意が必要だ。)
繰り返しになるが、売上を左右する要素は無数にある。売上という一つの従属変数に対して、独立変数があまりに多すぎる。
「何kgの小麦粉から何個のパンが作れるか」というのとは比較にならないくらい、「スタッフの提案力が上がれば売上が伸びる」という因果関係を確かめることは難しい。
そもそも「スタッフの提案力」を測定すること自体が不可能に近く、しかもそれが売上に寄与したかどうかを測定することは更に難しい。先程も述べたように、売上を左右する変数は他にいくらでもあるからだ。
だからこそ、少しでも問題を細かく分解して、何か具体的な案を思いつきやすくした方がいいというのが僕の考えだ。完璧な方策というのは存在しないが、成功確率の高そうな方策を探すことはできる。「ここが大事っぽい」という感覚を客観的に理解できる形で確かめるという意味でも、因数分解によって要素に分けることは有効だと思う。
《明確さは力だということ》
「問題を細かくしたほうがいい」と繰り返し述べるのは、その方が改善につなげやすいからだ。
例えば、スタッフの知識不足によって高額商品を上手く案内出来ていないことが問題だとする。その場合、インターネットで調べたり、知っていそうな人に聞くなどして知識を補えばいい。
「売上を伸ばそう」よりは「商品知識をつけよう」の方がわかりやすいし、取り組みの道筋も見えやすい。道筋が見えたほうがモチベーションも上がるだろう。
一般論として、抽象的な目標を立ててしまうと、具体的にどうしたらいいのかわからなくなる。「ビッグな男になりたい」とかもそうで、そもそも「ビッグな男とは何か」がわからないので目指し方も分からない。「月に100万稼ぎたい」とかの方が少しは考えやすい(月100万稼げばビッグなのかという問題は置いておくとしても)
とにかく、「何をするべきか」を明確にすることが改善に繋がる。繋がらない人もいるだろうけど、繋がりやすくはなる。明確さは力だ。
そしてその明確さを支えるのが、「問題を細かくする」ということだ。
問題を細かくする上で、因数分解的な思考が役に立つ。
《いくらでも応用できる》
これは別にアパレル業界に限ったことではない。多くの分野でこの考え方は応用できる。
例えば営業などをしている人もシビアに数字を求められるだろう。
成約件数○件という目標があったとして、
成約件数=アプローチ数×成約率
と考えて、過去の実績や同僚などと比較すれば、そもそもアプローチが少ないのか、沢山声をかけているのに成約に至っていないのかがわかる。
もし成約率が低いとなれば、話を聞いてもらえるにまでも至っていないのか、じっくり話し合った結果断られているのかを考えてみるのもいいだろう。自分がどの段階で手詰まりになっているのかを自覚できるまで考えるべきだ。
極端な話、ナンパなどでも理屈は同じだ。
そもそも声をかける回数が少ない人と、声をかけた結果断られている人ではやるべきことが違うはずだ。お茶まではいけてもその後はいけない場合もあるだろう。どの段階で課題があるのかを把握する上で、因数分解は役に立つ。
《あとはやるかやらないか》
因数分解というと数学的で難しく聞こえるが、考え方自体は至ってシンプルで、「要素の掛け算に分ける」というだけのことだ。数学の言葉ではあるが、数学の世界だけで切り離された概念ではなく、より広く捉えることで日常生活にも応用できる。
誰にでもできることだし、幅広い分野において同じ考え方を適用できることもわかっていただけると思う。
あとはやるかやらないかの問題であって、問題解決に対してどれだけ向き合っていくかという問題だろう。
今回の話で僕が伝えたいことは、「因数分解は数学の世界だけで完結するものではなく、日常生活にも応用できる」ということと、「義務教育レベルの知識でも敷衍していくことで大きな武器になる」ということなのだが、いかがだろうか。改めて中学の教科書を読み返してみるのもいいと思う。何か思わぬ発見があるかもしれない。
あなたにとっていいことがありますように。それでは、また。
放送大学在学中の限界サラリーマンですが、サポートは書籍の購入にあて、更に質の高い発信をしていきます!
