31.09 ベクトルの初歩（図形への利用 その３）

ベクトルの一意性を用いる解法についての話です。

ベクトルの一意性

平面上の任意のベクトル$${\vec{p}}$$は、与えられた２つの平行でないベクトル
$${\vec{a}\neq\vec{0}, \: \vec{b}\neq\vec{0}}$$によって

　　　　　　　　　　　　$${\vec{p}=k\vec{a}+\ell\vec{b} \:\: (k, \ell \in \mathbb{R})}$$

と表すことができます。しかもその表し方は１通りだけです。この１通りであることを一意性といいます。

これは、３つのベクトル$${\vec{a}, \: \vec{b}, \: \vec{p}}$$の始点を揃え、与えられた２つのベクトル$${\vec{a}, \: \vec{b}}$$を含む２本の直線を引き、$${\vec{p}}$$の終点を通りそれぞれの$${\vec{a}, \: \vec{b}}$$に平行な直線を引くと、$${\vec{p}}$$を対角線とする平行四辺形がただ一つできます。これが一意性であることに関係しています(※1)。

同様のことが空間ベクトルについても成り立ちます。つまり

空間内の任意のベクトル$${\vec{p}}$$は、与えられた同一平面上にない３つの空間ベクトル$${\vec{a}, \: \vec{b}, \: \vec{c}}$$によって

　　　　　　　　$${\vec{p}=k\vec{a}+\ell\vec{b}+m\vec{c} \:\: (k, \ell, m \in \mathbb{R})}$$

と表すことができます。しかもその表し方は一意 (一意的) です(※2)。

ベクトルの一意性は、１つのベクトルが２通り以上で表現されたとき、それらのベクトルの表し方が同じでなければならないことから、係数の値がただ１つ決まります。もちろん、使われているベクトルは同じものです。
この性質は線分の比を求めたりするときによく使われますが、ここでは、ベクトルを表す問題にしてあります。

例題１（平面図形編）

三角形△ABCにおいて、線分ACの中点をM、線分BCを２:１に内分する点をNとし、AN, BMの交点をＰとする。このとき、ベクトル$${ \overrightarrow{\mathrm{AP}}}$$を２つのベクトル$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AC}}}$$で表せ。

《考え方》まずは図示しましょう。

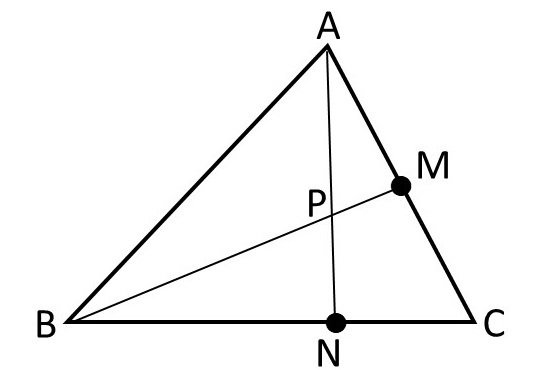
「$${ \overrightarrow{\mathrm{AP}}}$$を$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AC}}}$$で表す」には、何が分れば求められるかを考えます。理想は BP：PM または AP：PN ですね。

解くだけなら、メネラウスの定理または補助線で解決します(※3)。でもここの目的はベクトルの一意性の使い方を理解することです。

ベクトルの一意性を使うには、１つのベクトルが２つ以上の方法で表現されている必要があります。

とりあえず、$${ \overrightarrow{\mathrm{AP}}}$$を表したいのだから、BP：PM=s : (1-s) とすると

　　　　　　$${ \overrightarrow{\mathrm{AP}}=(1-s)\overrightarrow{\mathrm{AB}}+s\overrightarrow{\mathrm{AM}}=(1-s)\overrightarrow{\mathrm{AB}}+\dfrac{1}{\:2\:}s\overrightarrow{\mathrm{AC}}}$$

と表すことができます。さらにAP：AN=t : 1 とすると

　　　　　$${\overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AN}}=t(\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:3\:}\overrightarrow{\mathrm{AC}})=\dfrac{1}{\:3\:}t\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:3\:}t\overrightarrow{\mathrm{AC}}}$$

と表せます。これは「３点A, P, Nが同一直線上にある」と考えても同じ結果が得られます。
※ BP：PM=s : (1-s)と置ける理由は 31.07 をご覧ください。動画でも説明をしています。

$${\overrightarrow{\mathrm{AP}}}$$が２通りで表せましたが、ベクトルの一意性によって、表現の仕方が一致してなければなりません。つまり

　　　　　　　　　　$${1-s=\dfrac{1}{\:3\:}t \:\: かつ \:\: \dfrac{1}{\:2\:}s=\dfrac{2}{\:3\:}t}$$

でなくれはならないのです。これを解くと

　　　　　　　　　　　　　$${s=\dfrac{4}{\:5\:}, \:\: t=\dfrac{3}{\:5\:}}$$

を得るので、$${\overrightarrow{\mathrm{AP}}}$$を表している式の一方に代入すれば終わりです。

　　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\dfrac{1}{\:5\:}\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:5\:}\overrightarrow{\mathrm{AC}}.}$$ ▮

注：比を求める問題であっても、$${s, t}$$を求めるところまでは同じです。その後は

　　　　　　$${BP：PM=s : (1-s)=\dfrac{4}{\:5\:}:\dfrac{1}{\:5\:}=4:1}$$

または

　　　　　　$${AP：PN=t : (1-t)=\dfrac{3}{\:5\:}:\dfrac{2}{\:5\:}=3:2}$$

とすればいいのです。

解答例　BP：PM=s : (1-s) とすると

　　　　　　　$${ \overrightarrow{\mathrm{AP}}=(1-s)\overrightarrow{\mathrm{AB}}+s\overrightarrow{\mathrm{AM}}=(1-s)\overrightarrow{\mathrm{AB}}+\dfrac{1}{\:2\:}s\overrightarrow{\mathrm{AC}}}$$

と表せる。AP：PN=t : (1-t) とすると

　　　　　　$${ \overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AN}}=t(\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:3\:}\overrightarrow{\mathrm{AC}})=\dfrac{1}{\:3\:}t\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:3\:}t\overrightarrow{\mathrm{AC}}}$$

と表せる。$${\overrightarrow{\mathrm{AP}}}$$が平行でない２つのベクトル$${\overrightarrow{\mathrm{AB}}\neq\vec{0}, \: \overrightarrow{\mathrm{AC}}\neq\vec{0}}$$を使って
２通りで表せたが、ベクトルの一意性によって

　　　　　　　　　　$${1-s=\dfrac{1}{\:3\:}t \:\: かつ \:\: \dfrac{1}{\:2\:}s=\dfrac{2}{\:3\:}t}$$

でなければならない。これを解くと

　　　　　　　　　　　　　$${s=\dfrac{4}{\:5\:}, \:\: t=\dfrac{3}{\:5\:}}$$

を得るので

　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\dfrac{1}{\:5\:}\overrightarrow{\mathrm{AB}}+\dfrac{2}{\:5\:}\overrightarrow{\mathrm{AC}}.}$$ ▮

注：ベクトルの一意性を使うときは
　　　　　　「平行でない２つのベクトル$${\overrightarrow{\mathrm{AB}}\neq\vec{0}, \: \overrightarrow{\mathrm{AC}}\neq\vec{0}}$$」
を確認します。
もしも$${\overrightarrow{\mathrm{AB}}=\vec{0}}$$なら、どんな実数$${k}$$に対しても
　　　　　　　　　　　　$${ k\overrightarrow{\mathrm{AB}}=k\vec{0}=\vec{0}}$$
となってしまうからです。
特に記述式では減点対象になります。また、大学のセミナーでは条件を確認していないとツッコミが入ります。

例題２（立体図形編）

直方体ABCD-EFGHにおいて、対角線AGと△BDEの交点をＰとする。このとき、ベクトル$${ \overrightarrow{\mathrm{AP}}}$$を３つのベクトル$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AD}}, \: \overrightarrow{\mathrm{AE}}}$$で表せ。

《考え方》まずは図示。

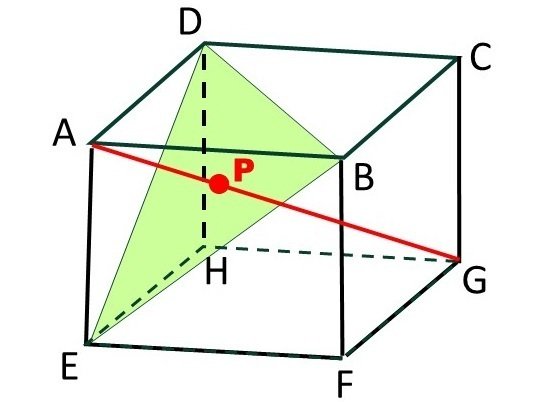
「$${ \overrightarrow{\mathrm{AP}}}$$を$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AD}}, \: \overrightarrow{\mathrm{AE}}}$$で表す」には、何が分れば求められるかを考えます。理想は AP：PG ですね。

３点A, P, Gが同一直線上にあるので

　　　　　　　$${ \overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AG}}=t(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}) \:\: (t\in \mathbb{R})}$$

と書けます。
※ AP：AG=t : 1 または AP：PG=t : (1-t) としても同じ結果を得ます。どの表現を使うかは好みです。

平面図形とは違い次の一手が難しいのですが、幸い、今はベクトルの一意性の使い方を学んでいるので、やることは分かっています。$${ \overrightarrow{\mathrm{AP}}}$$の別の表現を考えたいのです。

初見でこれに気づくのはかなり難しいと思います。ということは、比またはベクトルを表す１つの方法として「ベクトルの一意性」を使う方法があることを認識しておきましょう。

さて別の表現ですが、点Pは平面BDE上の点なので

　　　　　　　　　　$${ \overrightarrow{\mathrm{EP}}=r\overrightarrow{\mathrm{EB}}+s\overrightarrow{\mathrm{ED}} \:\: (r, s\in \mathbb{R})}$$

と表すことができます。「平面上のベクトルは、平行でない２つの零でないベクトルで表せる」ことを使いました。これは最初に述べたことで、一意性を除いた部分です。

「$${ \overrightarrow{\mathrm{AP}}}$$を$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AD}}, \: \overrightarrow{\mathrm{AE}}}$$で表す」のが目標なので、$${\overrightarrow{\mathrm{EP}}=r\overrightarrow{\mathrm{EB}}+s\overrightarrow{\mathrm{ED}}}$$を次のように変形します：

　　　　　　　　　$${ \overrightarrow{\mathrm{EP}}=\overrightarrow{\mathrm{EA}}+\overrightarrow{\mathrm{AP}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AP}}.}$$

同様に

　　　　　　　$${\overrightarrow{\mathrm{EB}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AB}},\quad \overrightarrow{\mathrm{ED}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AD}}}$$

と表せます。こらを代入して整理します。

　　　　　$${ \overrightarrow{\mathrm{EP}}=r\overrightarrow{\mathrm{EB}}+s\overrightarrow{\mathrm{ED}}}$$

　　$${\iff (-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AP}})=r(-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AB}})+s(-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AD}})}$$

　　$${\iff \overrightarrow{\mathrm{AP}}=r\overrightarrow{\mathrm{AB}}+s\overrightarrow{\mathrm{AD}}+(1-r-s)\overrightarrow{\mathrm{AE}}}$$

$${\overrightarrow{\mathrm{AP}}}$$が２通りで表せたので、以下は平面図形のときと同じようにして解けます。係数を比較すると

　　　　　　　　　　　　$${r=t, \: s=t, \: 1-r-s=t}$$

を得、前半２つの式を最後の式に代入すれば

　　　　　　　　　　　　　　$${1-t-t=t}$$

となるので $${t=\dfrac{1}{\:3\:}(=r=s)}$$ と求められます。

よって

　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AB}}+\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AD}}+\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AE}}}$$

となります。解答例は次の通りです。

解答例　３点A, P, Gが同一直線上にあるので、実数$${t}$$を用いて

　　　　　　　　$${ \overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AG}}=t(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}})}$$

と書ける。また、点Pは平面BDE上の点なので、２つの実数$${r, s}$$を用いて

　　　　　　　　　　　　$${ \overrightarrow{\mathrm{EP}}=r\overrightarrow{\mathrm{EB}}+s\overrightarrow{\mathrm{ED}}}$$

と書ける。ここで

　　　　$${\overrightarrow{\mathrm{EP}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AP}}, \quad \overrightarrow{\mathrm{EB}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AB}},\quad \overrightarrow{\mathrm{ED}}=-\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AD}}}$$

より

　　　　　$${ \overrightarrow{\mathrm{EP}}=r\overrightarrow{\mathrm{EB}}+s\overrightarrow{\mathrm{ED}}}$$

　　$${\iff \overrightarrow{\mathrm{AP}}=r\overrightarrow{\mathrm{AB}}+s\overrightarrow{\mathrm{AD}}+(1-r-s)\overrightarrow{\mathrm{AE}}}$$

となる。$${\overrightarrow{\mathrm{AP}}}$$が同一平面上にない３つのベクトル$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AD}}, \: \overrightarrow{\mathrm{AE}}}$$を使って
２通りに表せたので

　　　　　　　　　　$${r=t, \: s=t, \: 1-r-s=t}$$

でなければならない。これを解くと$${t=\dfrac{1}{\:3\:}}$$ であるから

　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AB}}+\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AD}}++\dfrac{1}{\:3\:}\overrightarrow{\mathrm{AE}}.}$$ ▮

注：立体図形の場合は、平面図形のときより一意性を使うための条件がかんたんです。でも平面と立体では条件が異なるのでなかなか覚えられないと思います。だから使う度たびに、間違っても気にせず条件を取り敢えず書いてみてから、条件を確認しましょう。そのうち覚えられます。

注２：以前少し触れているのですが、条件の部分はもっとかんたんに言い換えることができます。「線形独立 (一次独立)」を用いるのですが、大学以降の数学です(※4)。教科書や参考書によっては紹介されているようです。

※ 高校数学ではふつう学ばない専門用語などを使うと採点は厳しくなりがちです。「など」には定理も含みます。

例題が解けるようになったら、一意性を使う練習をしましょう。