31.07 ベクトルの初歩（図形への利用）

平面上または空間内のベクトルの続きです。三角形ABCとあった場合、平面上の図形と捉えても構わないし、空間の図形と捉えても構いません。
今回は、線分の内分点、中点、外分点および三角形の重心に関するものを扱います。

ベクトルは、向きと長さが等しいければ同じものと考えるので、１点を固定し、それを始点としたベクトルで考えることをよくします。

内分点と中点

例１　３点A, B, Cを頂点とする△ABCを考え、$${\vec{b}:=\overrightarrow{\mathrm{AB}}, \: \vec{c}:=\overrightarrow{\mathrm{AC}}}$$とし、線分BCを$${3:1}$$に内分する点を$${\text{P}}$$とするとき、$${\overrightarrow{\mathrm{AP}}}$$を$${\vec{b},\: \vec{c}}$$で表してみましょう。

AからPへの移動をA→B→Pと考えると
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BP}}}$$
となります。
$${\text{BP}:\text{PC}=3:1}$$なので
　　　　　　　　　　　　　$${\overrightarrow{\mathrm{BP}}=\dfrac{\:3\:}{4}\overrightarrow{\mathrm{BC}}}$$
と表せます。ここで
$${\overrightarrow{\mathrm{BC}}}$$は、BからCへの移動をB→A→Cと考えて
　　　　　　　　　　$${\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AC}}=-\vec{b}+\vec{c}}$$
です。以上をまとめると
　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BP}}}$$
 　　　　　　　　　　　  $${=\overrightarrow{\mathrm{AB}}+\frac{\:3\:}{4}\overrightarrow{\mathrm{BC}}}$$
　　　　　　　　　　 　  $${=\vec{b}+\frac{\:3\:}{4}(-\vec{b}+\vec{c})=\dfrac{\:1\:}{4}\vec{b}+\dfrac{\:3\:}{4}\vec{c}}$$
となります。▮

この考え方は基本で、修得したいものの一つです。
ただこの場合は、平面幾何の知識を利用すると最後の結果がかんたんに得られます。

（別の考え方）
点Pを通りベクトル$${\vec{b}}$$と平行な直線と線分ACとの交点をC'、点Pを通りベクトル$${\vec{c}}$$と平行な直線と線分ABとの交点をB'とします。

すると$${\overrightarrow{\mathrm{AP}}}$$は平行四辺形AB'PC'の対角線とみることができるので
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{AB'}}+\overrightarrow{\mathrm{AC'}}}$$
となります。ここで次のように着目すると

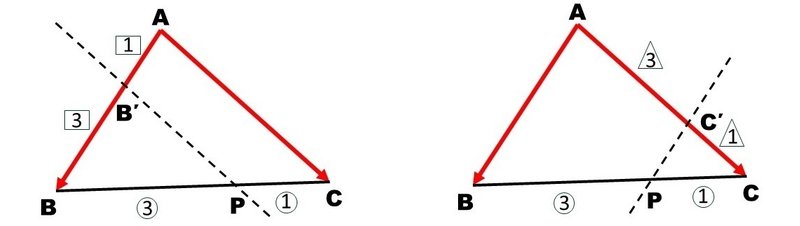
$${\text{B'P}/\!/\text{AC}}$$より
　　　　　　　　　　$${\text{BB'}:\text{B'A}=\text{BP}:\text{PC}=3:1}$$
となり
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AB'}}=\dfrac{\:1\:}{4}\overrightarrow{\mathrm{AB}}=\dfrac{\:1\:}{4}\vec{b}.}$$
同様に考えて
$${\text{AB}/\!/\text{C'P}}$$より
　　　　　　　　　　$${\text{AC'}:\text{C'C}=\text{BP}:\text{PC}=3:1}$$
となり
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AC'}}=\dfrac{\:3\:}{4}\overrightarrow{\mathrm{AC}}=\dfrac{\:3\:}{4}\vec{c}.}$$
よって
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AP}}=\dfrac{\:1\:}{4}\vec{b}+\dfrac{\:3\:}{4}\vec{c}.}$$ ▮

説明をしているので長く感じますが、図を見れば最後の式が書けます。

前半または後半の考え方を一般化すると次のようになります：

内分点に関する公式

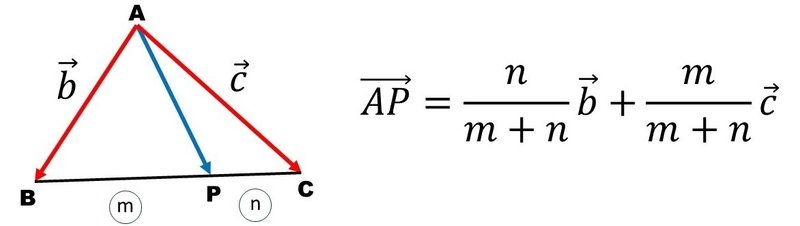
暗記をしてもいいですが、後半を理解すればかんたんに選られます。

問題　△ABCにおいて、線分BCの中点をMとするとき、$${\overrightarrow{\mathrm{AM}}}$$を$${\overrightarrow{\mathrm{AB}}, \: \overrightarrow{\mathrm{AC}}}$$で表せ。

問題の答え
　　　　　　　$${\overrightarrow{\mathrm{AM}}=\dfrac{\:1\:}{2}\overrightarrow{\mathrm{AB}}+\dfrac{\:1\:}{2}\overrightarrow{\mathrm{AC}}}$$
解説　内分の公式を使うなら、BM:MC=1:1と考えて、$${m=n=1}$$を当てはめます。後半の方法なら真ん中なのでそれぞれ半分です。▮

三角形の重心

例２　三角形△ABCにおいて、$${\vec{b}:=\overrightarrow{\mathrm{AB}}, \: \vec{c}:=\overrightarrow{\mathrm{AC}}}$$とし、三角形の重心を$${\text{G}}$$とするとき、$${\overrightarrow{\mathrm{AG}}}$$を$${\vec{b},\: \vec{c}}$$で表してみましょう。

この問題を解決するには、三角形の重心に関する知識が必要ですね。まずは中線ですが、中線とは頂点とその対辺の中点を結んだ直線のことで、重心とは三角形の３中線が１点で交わるその交点です。そしてその重心の性質は中線AGを２:１に内分します。

これらを踏まえると、重心の性質から
　　　　　　　　　　　　　$${\overrightarrow{\mathrm{AG}}=\dfrac{\:2\:}{3}\overrightarrow{\mathrm{AM}}}$$
と分かります。
MはBCの中点なので
　　　　　　　　　　　　$${\overrightarrow{\mathrm{AM}}=\dfrac{\:1\:}{2}\vec{b}+\dfrac{\:1\:}{2}\vec{c}}$$
です（問題の答えを参照）。
よって以上から
　　　　　$${\overrightarrow{\mathrm{AG}}=\dfrac{\:2\:}{3}\overrightarrow{\mathrm{AM}}=\dfrac{\:2\:}{3}(\dfrac{\:1\:}{2}\vec{b}+\dfrac{\:1\:}{2}\vec{c})=\dfrac{\:1\:}{3}\vec{b}+\dfrac{\:1\:}{3}\vec{c}.}$$ ▮

（別の考え方）例１の別解のように考えることもできます。次の図で理解できると思います：

ここで一旦、知識を確認しましょう。