
31.06 ベクトルの初歩(空間図形の話)
各自の直観に頼って、ベクトルの話を進めることも可能だと思うのですが、その直観はこれまでの生活の中で育まれるものなので、どうしても理解のできないことも出てくると思います。
多くの場合は直観でわかると思いますが、いざというときのために、論理を準備しておきます。高校数学では定義・公理・定理が曖昧に書かれていますが、ここでは明確にします。
なお、この話を読み飛ばしても、特に空間ベクトルで困ることはないと思います。高校数学の教科書 (昔の中学数学の教科書) で十分です。
大切なこと:実際に図を描いて読み進めると理解が深まります。
空間図形の話をすることにした動機
問題 正四角錐O-ABCDにおいて、辺OCの中点をMとするとき、線分ABおよび点Mを含む平面で立体を切断したときの切り口の図形を答えよ。また、その理由も述べよ(※1)。
切り口の図形は等脚台形です。ではその理由を説明できますか。
例えば
線分ABと平面OCDが平行なので、平面で切ったときの辺ODとの交点をNとすると、AB//NMである。AB//DCより、NM//DCとなる。したがってNはODの中点である。さて、△OBM≡△OANよりBM=ANである。以上から四角形ABMNは等脚台形である。▮
と説明できそうです。でもこの説明には欠陥があります。
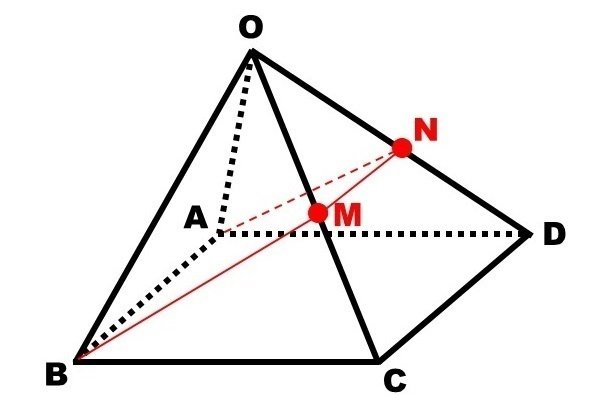
なぜ「線分ABと平面OCDが平行」なのでしょうか。
かんたんに説明できると思っていたのですが、なかなか出来ません。皆さんはできそうですか。
これを解決する過程で知ったのですが、空間内において、3本の直線$${\ell, \: m, \: n}$$において
$${\ell /\!/ m, \; \ell /\!/ n \implies m /\!/ n}$$
は、平面図形のときとは違い、説明するのはかんたんではありません。
「線分ABと平面OCDが平行」の結果を利用すると得られることが分かりました。それまでは直観的に空間図形を扱っていたので気づかなかったのです。
空間の幾何に要請するもの
平面の幾何では点と直線が基本図形でしたが、空間の幾何では点と直線そして平面が基本図形となります。これらは定義せずに使います。また、特別な場合を除き、大文字A, B, C …で頂点を、小文字a, b, c …で直線を、$${\alpha, \beta, \gamma}$$などのギリシャ文字で平面を表すことにします。
平面の幾何で要請した公理は、平面上で考えるときには引き続き用います。空間の幾何では、これに加えて次のことを要請します (公理)。このとき平面の幾何の公理に矛盾してはいけません。
①2点を結ぶ直線が唯1つ定まる。
②1本の直線とその直線上にない1点は平面を1つ定める。
③同一直線上にない3点は平面を1つ定める。
④1点を共有する2直線は平面を1つ定める。
⑤同一平面上にある2直線は1点で交わる、または平行である。
⑥2つの平面が1点を共有するなら、その2平面はその点を通る直線を共有する。
⑦ある直線を含まない平面は、その直線と1点より多く共有点を持たない。
※ 図を描いて確認してみると、当たり前と思われることばかりだし、覚える必要もありません。使うときにそのつど確認すれば十分です。
①は "2点は直線で結べる" という基本的要請です。
②~④は平面の決定条件です。
⑤の対偶をとると、平行でなく、交わらない2直線があれば、その2直線は同一平面上にないということです。このような2直線はねじれの位置にあるといいます。
⑥の2平面から得られる直線を交線といいます。
共有点を持たない2平面は平行であるといいます。
直線と平面が共有点を持たないとき、直線と平面は平行であるといいます。
注1 "ねじれの位置" は、同一平面上にない2直線とも言えるし、平行でなく、交わらない2直線とも言えます。分かりやすい方で理解してください。
注2 "平行" は2直線、2平面および直線と平面の関係で使われるので、何と何が平行なのかを確認しましょう。
平面の幾何については次をご覧ください。
問題1(基本用語の確認①)
次に当てはまるものをすべて答えよ。
1.直方体ABCD-EFGHにおいて
①直線ABとねじれの位置にある直線
②直線ABと平行な平面
③平面AEFBと平行な平面
2.正四角錐O-ABCDにおいて
①直線OAとねじれの位置にある直線
②直線OAと平行な平面
③直線ABと平行な平面
④平面OABと平行な平面
問題1の答え
1.①直線DH, CG, EH, FG ②平面EFGH, DHGC ③平面DHGC
2.①直線BC, CD ② ↓ ③平面OCD
②④四角錐の頂点でつくられる平面には存在しない
注意:1②③は素直な答え方の一つです。他の答え方として
②を平面EFGと答えても正解です。 ③を平面CGHDと答えても正解です。
2②④は捻くれた感じの問題と答えですが、基本用語を理解するには必要なことかと思い出題しました。テストでは出題されないと思います。
成す角(2直線、2平面、直線と平面)
2直線の成す角 (なす角) とは、2直線のつくる角のことです。
(注意) 交わらない2直線の場合は、平行移動させて交わるようにしたときの2直線のつくる角のことです。

上図の2直線$${\ell, \: m}$$の成す角は ● または▲です。なので、成す角$${\theta}$$に制限を付けて、$${0\leqq \theta \leqq \dfrac{\:\pi\:}{2}}$$(または 0度以上90度以下)とすることもあります。
※ これについては判断できるように書かれているものです。
2平面の成す角とは、交線上に任意の点を取り、その点を通る2平面上の直線の成す角のことをいいます。(下図参照)

直線と平面の成す角とは、与えられた直線$${\ell}$$と平面$${\pi}$$の共有点をPとする。点Pを通る平面上の直線たちと$${\ell}$$との成す角の中で最小の角のことをいいます。

垂直(2直線、2平面、直線と平面)
2直線$${\ell, \: m}$$の成す角が直角であるとき、2直線は垂直であるといい、記号で$${\ell \perp m}$$と書きます。特に、2直線が直角に交わるときは、直交するともいいます。
2平面$${\alpha, \: \beta}$$の成す角が直角であるとき、2直線は垂直であるといい、記号で$${\alpha\perp \beta}$$と書きます。2平面の場合は必ず交わるので、直交するともいいます。
直線と平面の場合も同様に定義しても良いのですが、"最小の角" というのが扱い難いので、次のように定義します:
直線$${\ell}$$が平面$${\pi}$$上のすべての直線と垂直であるとき、直線$${\ell}$$と平面$${\pi}$$は垂直であるといい、記号で$${\ell\perp\pi}$$と書きます。
注1:定義から、直線$${\ell}$$と平面$${\pi}$$が垂直であるとき、平面$${\pi}$$上の任意の直線と$${\ell}$$は垂直です。
注2:直線と平面が垂直であることをいいたいとき、定義に従って平面上のすべての直線と垂直であることを確認するのは実用的ではありません。有難いことに、「直線$${\ell}$$が平面$${\pi}$$上の交わる2直線と垂直であることが確認できれば、$${\ell\perp\pi}$$である」という定理 (直ぐ下) があります。
注3:平行$${/\!/}$$と垂直$${\perp}$$の記号は乱用されます。
定理(直線と平面の垂直条件)
直線$${\ell}$$が平面$${\pi}$$上の交わる2直線と垂直であれば$${\ell\perp\pi}$$である。▮
高校数学の教科書等では証明を省略し事実として認めますが、とてもよく使う定理なので、後ほど証明の流れを示します。やさしくないので幾何の証明が苦手な場合は飛ばしてください。
定理を使うと次のことが分かります。
例 正四面体ABCDにおいて、辺ABの中点をMとするとき、線分ABと平面CDMは垂直である。実際、△ABCは正三角形なのでAB⊥MC.同様に、△ABDにおいてもAB⊥MDとなる。▮

問題2(基本用語の確認②)
次に当てはまるものをすべて答えよ。
1.立方体ABCD-EFGHにおいて
①直線ABと垂直な直線
②直線ABと垂直な平面
③平面ABCDと垂直な平面
④2平面ABCDとABGHの成す角の大きさ (鋭角)
2.正四角錐O-ABCDにおいて
①平面ABCDと垂直な平面
②平面OACと垂直な直線
③平面OACと垂直な平面
問題2の答え
1①直線AE, AD, EH, DH, BF, BC, CG, FG ②平面AEHD, BFGC
③平面AEFB, BFGC, CGHD, AEHD ④$${\frac{\:\pi\:}{4}}$$(45度, $${\frac{1}{\:2\:}}$$直角)
2①平面OAC, OBD ②直線BD ③平面OBD, ABCD
空間内で垂線を引く方法(三垂線の定理)
問題 平面$${\pi}$$上にない点Pから$${\pi}$$に垂線PHを下ろせ。このとき、平面幾何の知識(平面上のある点から直線に垂線を引く作図、直線上の点を通る直線に対する垂線を引く作図)は仮定する。
この問題が解けるようなら、もうこのページから得るものはないと思います。最初に提示した問題も自力で解決できると思います。
答え 以下の手順で垂線が引けます。
①平面$${\pi}$$上に任意の直線$${\ell}$$を引く
②$${\ell,}$$Pを含む平面において、点Pから直線$${\ell}$$に垂線を下ろし、その足をAとする
③平面$${\pi}$$において、点Aを通り直線$${\ell}$$に垂線な直線$${m}$$を引く
④$${m,}$$Pを含む平面において、点Pから直線$${m}$$に垂線を下ろし、その足をHとする(完成)

$${\text{PH}\perp\pi}$$である理由
平面$${\pi}$$上の2直線とPHが垂直であることを示せば、定理から$${\text{PH}\perp\pi}$$であることがいえます。④から直線$${m}$$とPHは垂直なので、直線$${\ell}$$とPHが垂直であることを示せば良いですね。
②から$${\ell}$$⊥PAです。③から$${\ell}$$⊥$${m}$$です。したがって、定理から直線$${\ell}$$と平面PAHは垂直であることが分かります。
よって垂直の定義から、直線$${\ell}$$と平面PAH上の直線PHとは垂直であることが分かりす。
以上から、$${\text{PH}\perp\pi}$$であることが確認できました。▮
これは "三垂線の定理" と呼ばれているものの1つです。
三垂線の定理
① $${\text{PH}\perp\pi, \: \text{AH}\perp\ell \implies \text{PA}\perp\ell.}$$
② $${\text{PH}\perp\pi, \: \text{PH}\perp\ell \implies \text{AH}\perp\ell.}$$
③ $${\text{PA}\perp\ell, \: \text{AH}\perp\ell, \: \text{PH}\perp\text{AH} \implies \text{PH}\perp\pi.}$$ ▮
③が問題に対応します。
①②の証明は、問題の説明が理解できれば分かります。ポイントは
「直線$${\ell}$$と平面PAHは垂直である」
です。
三垂線の定理は、どういう仕組みかを理解すれば書き出せるようになります。でも暗記が好きな人は覚えても構いません。
例 立方体ABCD-EFGHにおいて、EGとFHの交点をOとするとき$${\text{AO}\perp\text{FH}}$$および$${\text{AG}\perp\text{FH}}$$であることが分かります。
※ 細かい部分は各自の課題とします。三垂線の定理が理解できれば、当たり前にしか見えなくなると思います。
実は、2平面AEGC, BFHDが垂直であることを示す方がらくです。
定理(直線と平面の垂直条件)の証明の流れ
定理 直線$${\ell}$$が平面$${\pi}$$上の交わる2直線と垂直であれば$${\ell\perp\pi}$$である。▮
平面$${\pi}$$上の交わる2直線$${m, \: n}$$を描き、交点をOとする。点Oを通り2直線に垂直な直線$${\ell}$$を描く。(与えられた仮定)
何を示せばよいか分かりますか。(証明はここが大事)
定義から、平面$${\pi}$$上の任意の直線が$${\ell}$$と垂直であることを示せばよいと分かります。
そこで任意の直線を描きますが、2直線の垂直の定義から、点Oを通る任意の直線を考えれば十分であることが分かります。$${m}$$または$${n}$$に重なる直線なら、何も示す必要はありません。なので重ならないように描き入れてください。
次に、描き入れた直線および2直線$${m, \: n}$$と交わるように、平面$${\pi}$$上の直線を描き、2直線$${m, \: n}$$との2交点をA, B (位置関係が逆でも構いません)、先の直線との交点をCとします。さらに、直線$${\ell}$$上に2点P, QをPO=OQとなるように取ります。(準備完了)
確認:直線OCは平面$${\pi}$$上の任意の直線です。
なので示すのは PQ⊥OC です。

これまでもそうでしたが、逆転の思考を続けます。
PQ⊥OC を示すには ∠POC=∠QOC を示せばよい。
∠POC=∠QOC を示すには △POC≡△QOC を示せばよい。
△POC≡△QOC を示すには PC=QC を示せばよい。
PC=QC を示すには △PAC≡△QAC を示せばよい。
△PAC≡△QAC を示すには PA=QA かつ ∠PAC=∠QAC が示せればよい。
PA=QA を示すには △PAO≡△QAO を示せばよく、これは示せる。
∠PAC=∠QAC を示すには △PAB≡△QAB を示せばよい。
△PAB≡△QAB を示すには PA=QA かつ PB=QB を示せばよい。
PA=QA はすでに示されている。
PB=QB を示すには △PBO≡△QBO を示せばよく、これは示せる。
長ーくなりましたが、これを逆に辿れば証明できます。
シャーロックホームズは「△PAO≡△QAO, △PBO≡△QBOより明らか」と言って相手を驚かし、ワトスン博士は「これらの流れをきいて、"Obvious!" と言うのです。
難しく感じるのは、視点をあちらこちらへと変えるからです。この中でもっとも難しいのは、△PAC≡△QAC が示せることに気づくことです。あとは難しくありません。長いだけです。
では確認します。
△PAO≡△QAO, △PBO≡△QBO は2辺挟角相等で確認できます。挟角は仮定 (前提) である$${\ell\perp m, \: \ell\perp n}$$から分かります。2辺相等は共通の辺およびP, Qの取り方(PO=OQ)からです。
残りは各自に任せます。
証明を完成させるよりも、むしろ、どのように考えたのかの方が大切だと思います。▢
参考文献
黒須康之介 著『平面立体 幾何学』(培風館)
寺阪 英孝 著『幾何とその構造』(日本評論社)
高校数学の検定教科書
この記事が気に入ったらサポートをしてみませんか?

