
29.01 微分の初歩(微分の動機 その1)
シリーズ29, 30 では多項式で表される関数の微分と積分を紹介します。内容的には高校数学Ⅱの微分と積分で、基本的な考え方と使い方を紹介します。
※この記事はほとんどすべて無料で読めます。
高校数学で学ぶ微分・積分は論理よりも直観に頼る説明になります。先人の微分と積分との関係の発見は、現代数学の見地に立つと、直観に頼ったものでした。その後の数学者たちが欠点を補い現在に至ります。数学史を学ばずとも、微分積分の本を読めば多くの数学者の名前が出てくるので気づくと思います。
シリーズ29, 30 はあまり細かいことを気にせず、全体像をつかみましょう。細かい部分は大学以降の数学で学びます。パソコンを使うために機械言語からはじめる人がいないように、まずは使ってみようという感じです。
注意:29.01~29.03は退屈かもしれないので、基本的なことに興味ない場合は読み飛ばしてください。
平均変化率
平均変化率はすでに紹介しています。中学数学で変化の割合と呼ばれているものです。詳しくは シリーズ15, 17 (マガジン3) をご覧ください。
確認(平均変化率)
集合 $${X}$$上で定義されている関数 $${y=f(x)}$$において、$${x}$$の増分に対する$${y}$$の増分比を平均変化率と呼びます。
$${x}$$が$${a}$$から$${b}$$まで変化するとき、$${x}$$の増分は $${b-a}$$であり、これに対する$${y}$$の増分は$${f(b)-f(a)}$$なので、平均変化率は式
$${\dfrac{f(b)-f(a)}{b-a}}$$
で表されます。関数 $${y=f(x)}$$のグラフで考えると2点$${(a, f(a)), \: (b, f(b))}$$を結ぶ直線の傾きを表しています。
例 関数 $${y=x^2 \:\: (x\in \mathbb{R})}$$において
$${x}$$が$${-2}$$から$${1}$$まで変化するときの平均変化率は
$${\dfrac{f(1)-f(-2)}{1-(-2)}=\dfrac{1^2-(-2)^2}{1-(-2)}=\dfrac{1-4}{1+2}=-1.}$$
$${x}$$が$${1}$$から$${-2}$$まで変化するときの平均変化率は
$${\dfrac{f(-2)-f(1)}{(-2)-1}=\dfrac{(-2)^2-1^2}{(-2)-1}=\dfrac{4-1}{-3}=-1.}$$
結果的に、$${x}$$が$${-2}$$から$${1}$$まで変化するときも$${1}$$から$${-2}$$まで変化するときも平均変化率は同じになります。
図形的に考えると、どちらも2点$${(-2, f(-2)), \: (1, f(1))}$$を結ぶ直線の傾きを考えることになるので当然です。
注:昨日の気温が18℃で今日が15℃であれば気温の変化量は -3℃ です。このように 18℃から15℃に変わったのなら $${15-18=-3}$$と計算するのが自然です(※1)。でも日常的には $${18-15=3}$$として3℃下がったと考えるのがふつうですね。
上の例で平均変化率が $${-1}$$なので減っていることを意味していますが、$${x}$$が$${-2}$$から$${1}$$まで変化するとき $${y}$$の値は減り続けているのでしょうか。
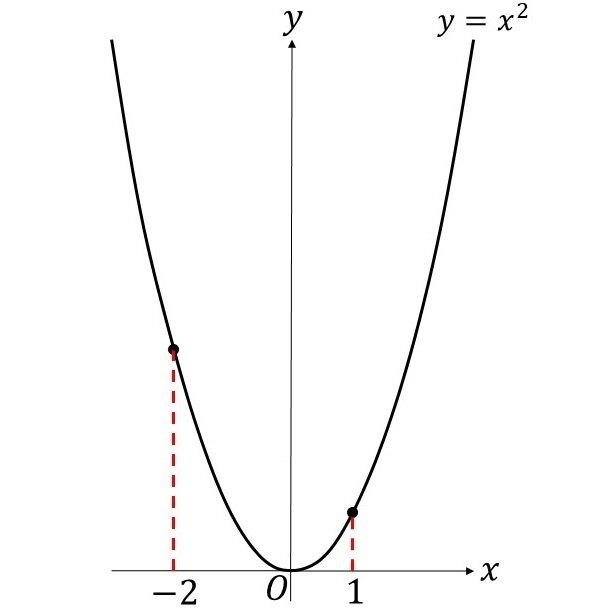
グラフをみて分かるように $${-2}$$から$${0}$$までは単調に減少し、$${0}$$から$${1}$$までは単調に増加しています。このことからも平均変化率が平均の変化率であることが分かります。
そこで気になるのは瞬間的な変化率です。感覚的には非常に狭い範囲での変化の様子のことです。
瞬間の変化率
上のグラフを見てみると、$${-2}$$の近辺, $${0}$$の近辺そして $${1}$$の近辺の変化率がそれぞれ異なっていることが読み取れると思います。
例えば $${-1}$$の近辺での変化率を知りたいと思ったら次のようにすれば求められそうです。$${-1}$$付近での $${x}$$の増分を小さくして
$${-1.1}$$から$${-1}$$までなら $${\dfrac{f(-1)-f(-1.1)}{(-1)-(-1.1)}=\dfrac{(-1)^2-(-1.1)^2}{0.1}=-2.1}$$
$${-1.01}$$から$${-1}$$までなら $${\dfrac{f(-1)-f(-1.01)}{(-1)-(-1.01)}=\cdots=-2.01}$$
$${-1.001}$$から$${-1}$$までなら $${\dfrac{f(-1)-f(-1.001)}{(-1)-(-1.001)}=\cdots=-2.001}$$
ここまで増分を小さくすれば十分に感じますが、もっともっと小さくして
$${\dfrac{f(-1)-f(-1.000001)}{(-1)-(-1.000001)}=\cdots=-2.000001}$$
のようにできます。直観に頼るのですが $${x=-1}$$での瞬間の変化率は $${-2}$$と考えるのが妥当でしょう。
いま$${-1.1}$$から$${-1}$$までのように $${-1}$$の左側で考えましたが、試しに $${-1}$$の右側でも考えてみましょう。
$${-1}$$から$${-0.9}$$までのとき $${\dfrac{f(-1)-f(-0.9)}{(-1)-(-0.9)}=\dfrac{(-1)^2-(-0.9)^2}{-0.1}=-1.9}$$
$${-1}$$から$${-0.99}$$までのとき $${\dfrac{f(-1)-f(-0.99)}{(-1)-(-0.99)}=-1.99}$$
$${-1}$$から$${-0.999}$$までのとき $${\dfrac{f(-1)-f(-0.999)}{(-1)-(-0.999)}=-1.999}$$
となり、瞬間の変化率は $${-2}$$に近づいていきます。なので$${x=-1}$$での瞬間の変化率は $${-2}$$と考えてよさそうです。この考え方が微分です。
次回、別の視点で瞬間の変化率を考えます。▢
※1 このように割り算や引き算は順番が大切です。掛け算や足し算は実数までの範囲で考えている限り交換可能なので順番に拘る必要はありません。
一方、例でみたように平均変化率は結果的に一致していますが、$${x}$$が$${-2}$$から$${1}$$まで変化するときの平均変化率を
$${\dfrac{f(-2)-f(1)}{(-2)-1}=\dfrac{(-2)^2-1^2}{(-2)-1}=\dfrac{4-1}{-3}=-1}$$
と求めるのは不自然です。増分を理解していないと考えらえるからです。
他方、2点$${(-2, f(-2)), \: (1, f(1))}$$を結ぶ直線の傾きを求める場合は
$${\dfrac{f(-2)-f(1)}{(-2)-1}, \quad \dfrac{f(1)-f(-2)}{1-(-2)}}$$
のどちらで計算しても構いませんが、教科書等では右が多いようです。数学の場合、左から右に増えるという考えがあるからだと思います。▮
余話
こういう話は大多数の子供たちが飽きてしまうようです。これまでの数学と違い、考え方ばかりでなかなか微分の計算に入らないからです。数学というと計算や解き方を覚え、テストで点数を取るのが目的となるので仕方ないのかもしれません。如何に速く答えを出すのかが受験競争で求められ、社会でもそれを求めています。
数学科に入ってくる学生の多くは数学を得意にしてきた人たちばかりです。教科書程度の問題なら瞬時に答えを出す上に、いろいろな定理や公式を知っていて巧みに問題を解いてしまいます。ロピタルの定理、コーシー・シュヴァルツの不等式、テイラーの定理など序の口です。
でも数学科に入ると授業では証明ばかりで、計算もなくはないのですが、これまでの数学と違うことに気づきます。実数が連続なことは知っているのにいちいち実数について述べたり、数字が縦横にたくさん並んでいる行列というものを扱ったりと意味不明です。教えている側からすれば数学する上での超基礎的な部分をやっているのですが、受け手側からすれば高校数学とのギャップに驚き、進学先を間違えたと感じるものです。学生の多くは数学が嫌いになり、そうでない一部の学生だけが数学の世界を謳歌します。
数学を謳歌する学生は入学前に数学の啓蒙書を読んでいたり、強者になると大学1,2年で学ぶ数学を読んでいたりします。余程のことがない限り、3年次には追いつくものなので気にする必要はありません。
学部時代は他学科だったけど、大学院から数学を専攻する人もいます。物理学科出身の人は精密な理論に惹かれたと言ってました。他に、ある数学者の自伝を読んで代数学に興味を持ち代数を独学した人、イプシロン・デルタ論法の哲学的な部分に興味を持ったという人、経済学で数学を学んで興味を持ったという人、教育学部からの人もいます。工学部の機械科では数学をかなり使うそうです。
数学科は理系に区分されていますが、私のように物理オンチの人も少なくないようです。
試験でない限り速く問題を解くことは求められません。大学以降の数学は、たとえ受験数学が制限時間内で解けなくても、教科書で扱っているくらいの計算力と教科書を読み進められる (節末問題が解ける) 力があれば対処できると思います。身構えたりせず、これからも数学をたのしみましょう。▮
最後になりますが、マガジンを購入してくれるとうれしいです。マガジン1は無料です。
これより先は特にありません。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?

