
2023共通テスト数学IAの各問の正答率を見ていきます
こんにちは。こもくです。
少し前の話になりますが、2023同年1月に行われた共通テストについて、大学入試センターが小問ごとの正答率を公表しました。
「数学IAの平均点は55点!」というざっくりとしたデータではありません。
「数学IAの大問1(ア)を正解した人は60%!」というかなり細かいデータです。

問題ごとの正答率が大学入試センターから公表されたのは初めて見ました。
予備校の中には受験生に頼んでこのデータを集計しているところもあるようですが、公表はあまりされていないように思います。Z会が少し公表しているくらいでしょうか。
要するに、問題ごとの正答率は貴重なデータということです。
本記事ではこのデータを参考に、共通テスト数学IAにおいて取りやすいところや差がつくところなどを見ていきたいと思います。
はじめに
本記事では令和5年度の共通テスト数学IAを取り扱います。問題は以下リンクから見ることができます。
問題を片手に、本記事を読み進めてみてください。
なお、解説は東進ハイスクールのWebサイトなどに載っています。
大問1
(アーエ)

絶対値混じりの不等式です。正答率が高めなのは一番はじめの問題ということもあるでしょうね(解けるまで考えたみたいな)。
(オーク)

(アーエ)のxが少し複雑に置き換わり、その後少々の変形を求められる問題ですが、正答率ががくんと落ちています。「よって」でつながっている時はその前の事柄を使う意識が大事ですね。
(ケーコ)

正答率がさらに下がります。(ク)までの不等式を使わず、等式のみの処理です。
最後の文章「〜であることが、等式➀、②、③の左辺を展開して比較することによりわかる」というところを読めば、(ク)までの話は関係なく、この問題は等式➀、②、③に着目して解くことがわかります。
問題の前の文章だけでなく、後の文章にもしっかり注目したいですね。
(サーシ)

三角形ABCの内部に点O入るのか入らないのかという細かい論点はありますが本問を解く上ではあまり関係なく、(サ)は正弦定理で一発、(シ)はsinとcosの関係式で一発・・・なはずですが正答率が意外と低いです。正弦定理の使い方や鈍角の意味がわからなかった受験生がまあまあいたようですね。
(スーソ)

円に内接する三角形の面積が最大になる時の問題。ここまでで一番の難所かもしれません、正答率は低め。
(ス)ができれば(セーソ)もすぐに出るように思いますが、意外と落差があります。(ス)は選択式の解答なので、ヤマカンで当たった人がある程度いたのでしょうね。
(タート)

リード文で球が出てきて不穏ですが、(タート)は完全に平面の話です。余弦定理と三角形の面積。リード文だけ読んで問題の難しさを判断しないようにしたいです。
(サ)の正弦定理、(ターチ)の余弦定理、正答率がともに8割を切っています。こういう基本定理はしっかり確認しておきたいですね。
(ナーハ)
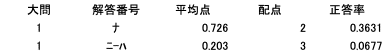
間違いなくここまでで最難問。(サーソ)の平面での話を空間での議論に拡張しています。何が何だかわからなかった受験生も多かったのでは。(ニーハ)は目標点次第では一旦捨てるのもありでしょう。
(ナ)の正答率は少し高いのは、選択式の解答ゆえ何となくであてた人もいるからでしょうか。一つだけ特徴的な選択肢ですし。受験当日は勘でも何でもあっていればそれでよしです。とりあえずマークは全部埋めましょう。
大問2
(アーウ)

共通テストを象徴するクソ長リード文の登場です(データの分析の長文はセンター試験でもありましたが)。長々書いているくせに、"52市"という情報以外は要らないという。
データの総数をリード文に混ぜるのはよくあることなのでそこだけはしっかり読みましょう。
基本的な問題ということもあり、正答率は高めです。第1四分位数のように"数"の問題よりも四分位範囲のように"範囲"に関する問題の方が正答率は下がる印象です。(ウ)のような範囲の幅の問題は、演習を解いておく必要があります。演習しておけば解けます。
(エ)

正答率90%超え。本問は答えがわかりやすかったのもあるでしょうが、箱ひげ図の問題はしっかり取りたいですね。
(オ)

分散の定義を問うてるだけの問題ですが正答率は意外と低め。言葉の定義はしっかり確認しておきたいです。
(カ)

相関係数の定義さえ覚えていればあとは計算の問題。正答率は7割程度。
結果的には、リード文はあまり読む必要がないですね。
(キーコ)

共通テストを象徴する長文問題。リード文は読み飛ばせますが、「仮定」は一文も読み落とせない仕様です。
設定を厳密にする必要があるので長文になるのは仕方ないといえば仕方ないですが、解く側にしたら嫌な話です。
読み取ってさえしまえば本問は「二次関数の決定」「二次関数の頂点の算出」という基本問題ですが、問題自体の簡単さに比べると正答率が低めの印象。
(サ)
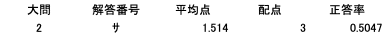
頂点のx座標の比較の問題。これは解説を聞けば誰しもがわかる問題だと思いますが、四択問題にも関わらず正答率は50%と低め。受験生が長文の読み取りに苦労している様子が伺えます。
(シーソ)

これも解説があればただの代入問題であることに納得できると思いますが、いかんせん設定が複雑なため正答率が低め。「問題文をしっかり読み取れれば実は単純な問題」であることは共通テスト数学の大きな特徴です。
(ターチ)

二択と四択の完答問題。概ね確率通りの正答率で、かなり低め。これも解説を聞けば「ああ、そういうことか!」とすぐなるであろう問題ですが、同じく正答率の低かった(シーソ)の解答を使うのが厳しかったですね。
大問3
(アーウ)

本大問は場合の数より出題。大問2に比べてリード文も短く、設定も理解しやすいです。正答率高め。
(エーオ)

正答率高め。(アーウ)より高いのには少し驚きました。
(カーキ)

少しづつ設定が凝ってきたため、正答率も落ちてきています。
(クーケ)
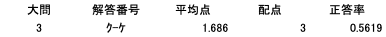
(カーキ)とほぼ同じ正答率。考え方が掴めてきた人はスイスイいけてそうですね。
(コース)

ほぼ繋がっている問題ですが、(コ)に比べて(サース)の正答率は低め。(コ)が五択問題だったのでとりあえずマークして当たった人がいるのでしょうね。わからなくてもマーク、本当に大事です。
(セーチ)

「ここまで誘導付きでやってきたけど、誘導なくても再現できるよね?」という問題。これも共通テストの大きな特徴です。正答率は当然低め。
大問4
(アーイ)

さて、整数問題です。462と110の両方を割り切れる"素数"を求める問題。最大公約数の22もマークにはまってしまうのが罠でした。まずまずの正答率。
(ウーカ)

直接的に言葉は出てきませんが、要するに最小公倍数を求める問題。正答率高め。
(キーシ)
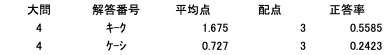
整数問題なのに式が一切与えられていないので、自分で式を組み立てていく必要がありました。繋がっている問題ではありますが、(ケーシ)の問題は難しかったようですね。
(スーチ)

最小公倍数と最大公約数を求める問題。時間的に苦しかったであろうことも考えると、正答率は高めといってよいでしょう。
(ツーナ)

ただの最小公倍数を求める問題でした。(スセソ)と(タチ)を前提にしているのでそれらより正答率は当然低め。
(ニーノ)

「これらのことと、〜であることから〜」と本大問を総括する問題。難しいし、何より時間がなかったでしょう。正答率は超低め。
大問5
(アーイ)

参考図しか与えられておらず、完成図は自分でかく必要があります。時間に追われながら冷静に丁寧に図をかくのは本当に大変です・・・。ただ、本問は接線という言葉から90度を連想できればそれでOKでした。正答率は高め。
(ウ)

これは図を正確にかけないと解けない問題。正答率が下がってきました。
(エーオ)

この辺はもうとりあえずマークだけした人も多そうですね、時間的な問題で。ともに五択問題ですが正答率は低めです。
(エ)から(オ)を求めるはずなのに(オ)の方が正答率が高いですね。ちなみに(オ)の答えは③です、適当にマークする際は③にする人が多いのでしょうかね。
確かに困ったら③っていうアドバイス(?)はよくある話です。
(カ)

厳密に求めるのであれば(エーオ)が前提になっているにも関わらず、正答率はかなりアップ。図を正しくかけていれば精度の高い予測ができたことの証左でしょうか。
最後の一文「この円が点(ウ)を〜」という文では何も求める必要がなさそうで一安心。
(キ)

問題が切り替わっていよいよ最後の小問。手順1とは直線の引き方を変えたみたいです。
本問は(エ)とほぼ同じ問題。正答率も同じくらい。
(クーサ)

さあ、最終問題。正答率は当然のごとく低め。厳密に求めていくと難しいですが、図を正しくかけていて(1)との繋がりを理解していれば、「細かいことは知らないけど多分この四点が同一円周上にあるのだろう」みたいに"何となく"解ける問題でもあります。とにかく時間に追われる共通テストでは必要以上に考え込まずに時には割り切ることも大事です。
大問ごとの平均点

大問1と大問2に関しては平均点がいくつでも平等ですが、選択式問題で差が出ているのはどれを選ぶかで少し運命が違ったことを意味しています。本年は場合の数と整数の選択がよかったということでしょうか、完全に結果論ですけども。
大問5は選択問題が多めの構成だったので、それを見た受験生が「時間がもうないから選択問題が多くて勘でもワンチャンある大問5にしよう!!!」と駆け込んだ結果平均点が少し下がった可能性もあるように思います。
共通テスト数学IAの直前期の勉強法
本記事の投稿日は2023年12月2日で、いわゆる直前期にあたります。応援の意味も込めて、勉強法のお話を最後にしておきます。
受験生が直前期にやることの選択肢は、大きく分けて三つになります。
1.センター試験の過去問
2.共通テストの過去問
3.共通テストの予想問題集
それぞれ使い方を考えてみます。
1.センター試験の過去問
「共通テストを戦う上でセンター試験の過去問をやることに意味があるのか」というのは賛否両論です。
「センター試験の過去問を20年分解けと言われた」
「傾向が違うから、センター試験の過去問を解くのは意味がないと言われた」
などの学生の声を現場で聞きました。
私の今のところの結論としては以下になります。
センター試験の過去問は時間を測って通しで解く必要はない。
苦手分野の問題集として使うとよい。
センター試験と共通テストでは時間の制約が全然違い、共通テストの方がーー主に文字数の問題でーー俄然キツイので、センター試験の過去問を60分測って通しで解くことにはあまり意味を感じません。
ではセンター試験の過去問を解くことには意味がないかというとそうでもなくて、苦手分野を潰す上でこの上ない問題集です。
例えば二次関数が苦手であれば、センター試験の過去問の二次関数の問題だけをひたすら解くということです。
センター試験と共通テストは、問題の魅せ方が違うだけで、問われていること自体は似通っている部分があります。その"問われていること自体"を、まずは問題文がシンプルなセンター試験の過去問を通して、解けるようになろうということです。
そもそもなぜ共通テストの対策にセンター試験の過去問を使うか否かが議論になるかというと、共通テストの過去問だけでは圧倒的に数が足りないからです。センター試験の過去問の数の多さを生かして、苦手分野を潰していきましょう。
2.共通テストの過去問
どういう状況でもこれは必ずやることになります。最優先です。最低でも本試3回、できれば追試3回も解いて本番に臨みましょう。
※追試まで収録されている書籍は意外と少ないので、問題と解答は大学入試センターで見て、解説はネットで探すという感じになります。
問題リンク
解説参考リンク
3.共通テストの予想問題集
大手予備校が予想問題と冠して出している書籍です。中には、本試の過去問も掲載されているものもあります。
これは70分の時間を測って通しで解きたいものです。
上で正答率を見てきましたが、
"問われていること自体は基本定理なのに、問題の言い方が複雑なせいで正答率が低い"
という問題がいくつもありました。問題文の長さや読解に慣れるためには共通テスト用の演習を積む必要があります。
特別な苦手分野ある場合はセンター試験の過去問が優先されますが、自分の中で満遍なく取れるようになってきたら、あとは予想問題集で共通テスト用の頭に仕上げていくのがよいと思います。
ちなみに、全教科の予想問題が入った"パック"というものも毎年発売されています。
私は自身が受験生の時、試験本番の一週間前に、試験本番の時間割通りにパックを解いて本番に備えました。この使い方がおすすめです。有用なリハーサルになります。
まだ受験が先の人に向けての勉強法
上で直前期の勉強を紹介しましたが、現在高校一年生や二年生で、受験までまだ時間がある人に向けてもおすすめの参考書・問題集を紹介しておきます。
ど定番ですが黄チャートがおすすめです。
チャート式の問題集はその厚さが驚異的ですが、何も一気に全問をやる必要はありません。
各問題の難易度が五段階評価されているので、一周目は難易度1と2、二周目はその復習に難易度3を加える、といったようにまずは難易度が低い問題から段階的に手をつけていく使い方をお勧めしています。
また、解く順番も頭からである必要はなく、苦手単元からやっていけばよいです。
このようにしておくと、少し気が楽に取りかかれると思います。
なお、持ち歩きが重くて大変な場合は分解という手があります。
まとめ
頑張れ受験生!合格を祈っています!

この記事が参加している募集
いかんせん低年収男ですので記事を気に入っていただけたらサポートしていただけると本当に嬉しいです。どうぞよろしくお願いいたします。
