3度の作図

中学1年のとき、なぜか作図にハマっていました。

今回はそのときに見つけたお話をしようと思います。

問題

$${3^{\circ}}$$は作図可能である。
また、角の2倍は作図可能なので、3の倍数の角度は作図可能である。

今回は$${3^{\circ}}$$の作図方法を紹介します。

作図のルール

定規とコンパスのみで作図する。

正五角形の作図

正五角形の対角線の長さ

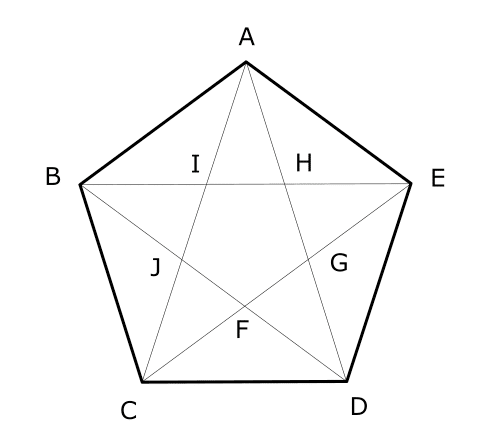
一辺の長さが1の正五角形を考える。

三角形ABJと三角形ACDは相似である。また、三角形DJCは$${\text{DJ} = \text{DC} = 1}$$の二等辺三角形である。

よって、対角線ACの長さを$${x}$$とすると、

$$
\begin{split}
\text{AB}:\text{AC} &= \text{BJ}:\text{CD} \\
1 : x &= x-1 : 1
\end{split}
$$

より、

$$
\begin{split}
x(x-1) &= 1 \\
x^2 - x + 1 &= 0 \\
x &= \frac{1\pm \sqrt{5}}{2}
\end{split}
$$

$x>0$より、

$$
x = \frac{1 + \sqrt{5}}{2}
$$

となる。

正五角形の作図方法

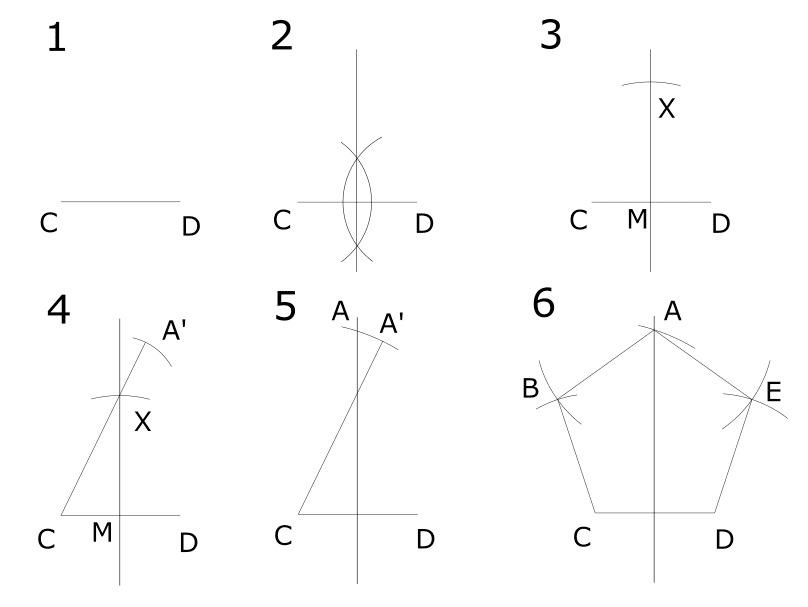
1. 1辺CDを設定する。

2. 線分CDの垂直二等分線を引く。

3. その垂直二等分線上にCD=MXとなる点Xをとる。

4. 直線CX上にCM=XA'となる点A'を図のようにとる。

5. 2で引いた垂直線二等分線上にCA'=CAとなる点Aをとる。

6. AB=BC=CD=DE=EAとなるように点Bと点Eをとる。AB→BC→CD→DE→EAで線を結ぶ。

正五角形になる理由

CDの長さを1とする。このとき、

$$
\text{MX}=1, \text{CM} = \frac{1}{2}
$$

なので、三平方の定理より、

$$
\begin{split}
\text{CX} &= \sqrt{1^2 + \left(\frac{1}{2}\right)^2} \\
&= \frac{\sqrt{5}}{2}
\end{split}
$$

$${\text{XA}' = \text{XA} = \frac{1}{2}}$$ より、

$$
\text{AC} = \frac{1+\sqrt{5}}{2}
$$

これで、対角線ACを作図することが出来たので、$${\text{BA}=\text{BC}=1}$$となる点Bと$${\text{EA}=\text{ED}=1}$$となる点Eを作図すると五角形ABCDEは正五角形となる。

3度の作図

以下を利用して作図する。

• 正五角形の内角は$${108^{\circ}}$$

• 正六角形の内角は$${120^{\circ}}$$

作図方法

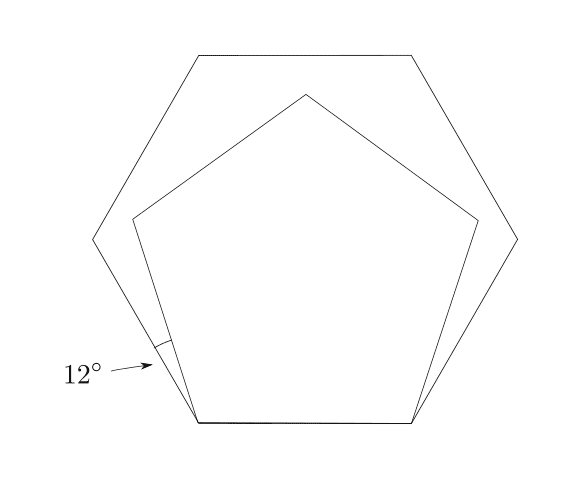
1. 正六角形を作図する。

2. 1で作図した正六角形の一辺を利用して、正五角形を作図する。

3. 正五角形と正六角形の間に出来た角度は$${120-108 = 12^{\circ}}$$。

4. $${12^{\circ}}$$の角の二等分を2回行うと$${3^{\circ}}$$となる。

最後に

今年の数学に関しての投稿は今回で終えたいと思います。
また来年ぼちぼち書いていこかと思います。

今年8月ごろからnoteを始めてほぼ週一で投稿してきました。(たまに、コメント投稿で誤魔化しているけど、、、)
これまでの記事を読んでくださった方、ありがとうございます。
来年は週一投稿はやめ、何か書きたくなった時、のんびり投稿していこうかと思っています。

---

最後まで読んでくださりありがとうございます。

少しでもコメの記事が面白そうだなーと思ってくれた方はフォローやスキをお願いいたします。