面積1〜円の面積2〜

この記事は上の記事の続きとなります。

まずはこれからお話しすることの流れを書こうと思います。

後半はややこしい内容になっているので、難しいなと思った方は「ふーん」という程度で読み流ししていただければと思います。
雰囲気だけでも伝わっていると嬉しいです！！

流れ

• $${r}$$：半径

• $${n}$$：円の分割数

• $${\pi}$$：円周率

とする。

図1

円を$${n}$$分割して張り合わせ、図1のように2つの平行四辺形を作る。

ただし、注意しておきたいのは、図1のような補助線は円の分割数が奇数だと平行四辺形にならなく台形になってしまう。そのため、今回は円の直径で分割すると考える。そうすることにより円の分割数は偶数となり図のような平行四辺形を作ることが可能である。

目標としては、円をものすごく分割すれば(つまり$${n}$$が十分に大きい数であれば)、「青い平行四辺形」と「赤い平行四辺形」が一致し、その平行四辺形は横の長さが円周の長さの半分、高さが半径なることである。

三角比

まずは三角比がどういうものだったかというのを見ていきたいと思います。

定義

$$
\sin \theta = \frac{a}{c}
$$

$$
\cos \theta = \frac{b}{c}
$$

$$
\tan \theta = \frac{a}{b}
$$

例

以下のような直角三角形を考える

図より、

$$
\sin 30^{\circ} = \frac{1}{2}
$$

$$
\cos 30^{\circ} = \frac{\sqrt{3}}{2}
$$

$$
\tan 30^{\circ} = \frac{1}{\sqrt{3}}
$$

今回はやらないがこの後使うため、三角比の拡張により

$$
\sin 0^{\circ} = 0
$$

$$
\cos 0^{\circ} = 1
$$

$$
\tan 0^{\circ} = 0
$$

となる。

---

いよいよ、平行四辺形が一致するかどうかのお話しをしていこうと思います。

ステップ1

まず、図1の青い平行四辺形について考える。

高さについて

図2

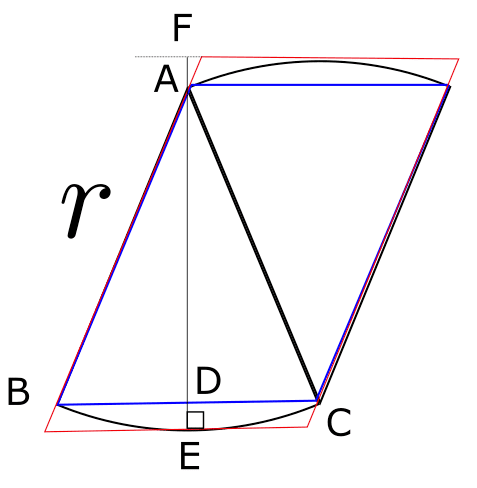
図1の青い平行四辺形の高さは図2の線分ADの長さと同じである。

$$
\cos \frac{180^{\circ}}{n} = \frac{\text{AD}}{\text{AB}} = \frac{\text{AD}}{r}
$$

より、

$$
\text{AD} = r\cos \frac{180^{\circ}}{n}
$$

横の長さについて

図1の青い平行四辺形の横の長さは図2のBCの長さの$${\frac{n}{2}}$$倍である。

$$
\sin \frac{180^{\circ}}{n} = \frac{\text{BD}}{\text{AB}} = \frac{\text{BD}}{r}
$$

より、

$$
\text{BC} = 2\text{BD} = 2r\sin \frac{180^{\circ}}{n}
$$

よって、図1の青い平行四辺形の横の長さは

$$
\frac{n}{2} \times \text{BC} = \frac{n}{2} \times 2r\sin \frac{180^{\circ}}{n} = rn\sin \frac{180^{\circ}}{n}
$$

ステップ2

図1の赤い平行四辺形について考える。

図3

高さについて

図1の赤い平行四辺形の高さは図3の線分FEの長さと同じである。

$$
\text{FE} = \text{AE} + \text{AF}
$$

であり、$${\text{AE} = r}$$より線分AFの長さを求めればいい。図3のAFとDEは同じ長さで、

$$
\text{DE} = \text{AE} - \text{AD}
$$

である。線分ADの長さは図1の青い平行四辺形の高さと同じなので、

$$
\text{DE} = r - r\cos \frac{180^{\circ}}{n}
$$

よって、

$$
\text{FE} = r + r - r\cos \frac{180^{\circ}}{n} = 2r - r\cos \frac{180^{\circ}}{n}
$$

となる。

横の長さについて

図1の赤い平行四辺形の横の長さは図1の青い平行四辺形の横の長さと同じなので、

$$
rn\sin \frac{180^{\circ}}{n}
$$

である。

分割数を十分大きくしてみる

まず、今回は分割数を偶数にするので

$$
n = 2k\ \ \ (k = 1,2,3,\dots)
$$

とする。

このとき、図1の青の平行四辺形の高さは

$$
r\cos \frac{180^{\circ}}{n} = r\cos \frac{180^{\circ}}{2k} = r\cos \frac{90^{\circ}}{k}
$$

図1の赤の平行四辺形の高さは

$$
2r - r\cos \frac{180^{\circ}}{n} = 2r - r\cos \frac{180^{\circ}}{2k} = 2r - r\cos \frac{90^{\circ}}{k}
$$

図1の青と赤の平行四辺形の横の長さは

$$
rn\sin \frac{180^{\circ}}{n} = 2rk\sin \frac{180^{\circ}}{2k} = 2rk\sin \frac{90^{\circ}}{k}
$$

となる。

高さについて

$${k}$$を十分に大きくすると$${\frac{90^{\circ}}{k}}$$は$${0^{\circ}}$$に近づいていくため

$$
\lim_{k\to \infty} \cos\frac{90^{\circ}}{k} = \cos0^{\circ} = 1
$$

よって、図1の青い平行四辺形の高さは

$$
\lim_{k\to \infty} r\cos\frac{90^{\circ}}{k} = r\cos0^{\circ} = r
$$

図1の赤い平行四辺形の高さは

$$
\lim_{k\to \infty} \left(2r - r\cos \frac{90^{\circ}}{k}\right) = 2r-r\cos 0^{\circ} = 2r-r = r
$$

なので円の分割数を十分大きくすると、図1の青い平行四辺形の高さと図1の赤い平行四辺形の高さは等しくなっていき、長さは半径と等しいことがわかる。

※ ちなみに分割数を十分大きくすると、平行四辺形の角度は90度になるため長方形になる。

横の長さについて

これが厄介である。

これを調べるためには

$$
\lim_{k\to \infty}k\sin \frac{90^{\circ}}{k}
$$

を求める必要がある。

---

次回に続く

最後に

次回は三角関数の極限

$$
\lim_{k\to \infty}k\sin \frac{90^{\circ}}{k}
$$

についてお話しして、円の面積が

半径×半径×円周率

であることを確かめて、円の面積のお話しは終わろうと思います。

最後まで読んでくださりありがとうございました。