忙しい人のための中学数学【式の展開・因数分解（計算のルール編）】

〜今回のテーマ〜
多項式の分配法則や乗法の公式等、展開のやり方を覚えよう。

その他の単元や計算問題はこちら

↓　↓　↓

はじめに

　このシリーズでは、各教科・各単元に登場する基本事項（用語やその定義、公式等）を中心にまとめていきます。
　現役中学生・高校生の軽い予習・復習、テスト勉強の最終確認はもちろん、「社会人枠で受験することになったから入試対策をしたい」、「子どもの勉強をサポートしてあげたい」等といった大人の皆さんもよろしければご活用ください。

　どの単元の学習でも基本を理解し、問題の中で使いこなせるようになることは、とても大切なことです。ある単元で学習したことが、別の単元で活かされることもたくさんあります。1つ1つ積み上げていきながら、土台を固めながら学習を進めていきましょう！

※できるだけ「わかりやすく」を目指していますが、今回のシリーズはあくまでも「忙しい人のための」シリーズなので、細かい部分まではまとめきれないこともあります。「もっと掘り下げて学習したい！」という人は、各自教科書や参考書、問題集等を活用しましょう。

　文字ばかりで難しく感じるなぁという人は、声に出して読んでみることをオススメします！

多項式と単項式の乗法・除法

　多項式×単項式の計算や単項式×多項式の計算は、以下の画像のように分配法則を用いて解きます。

多項式×単項式　↓

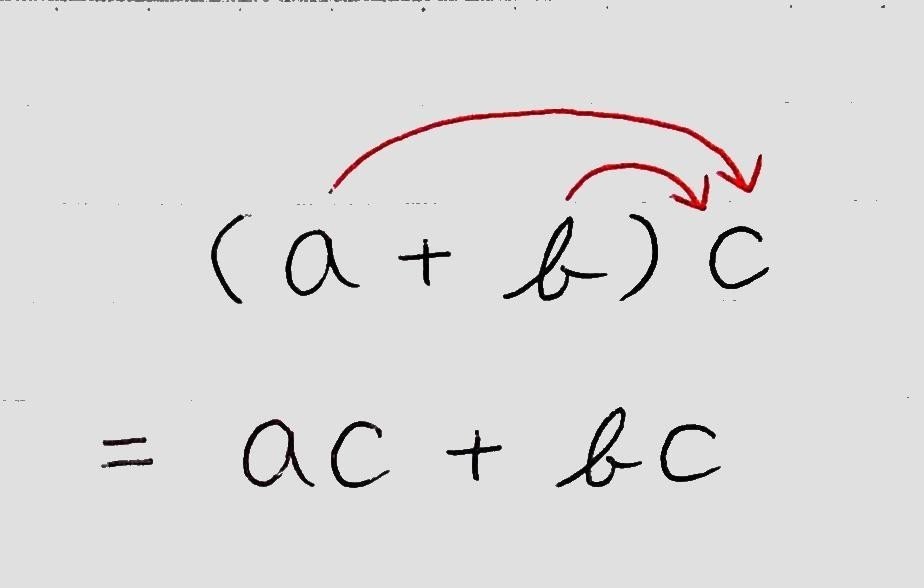
単項式×多項式　↓

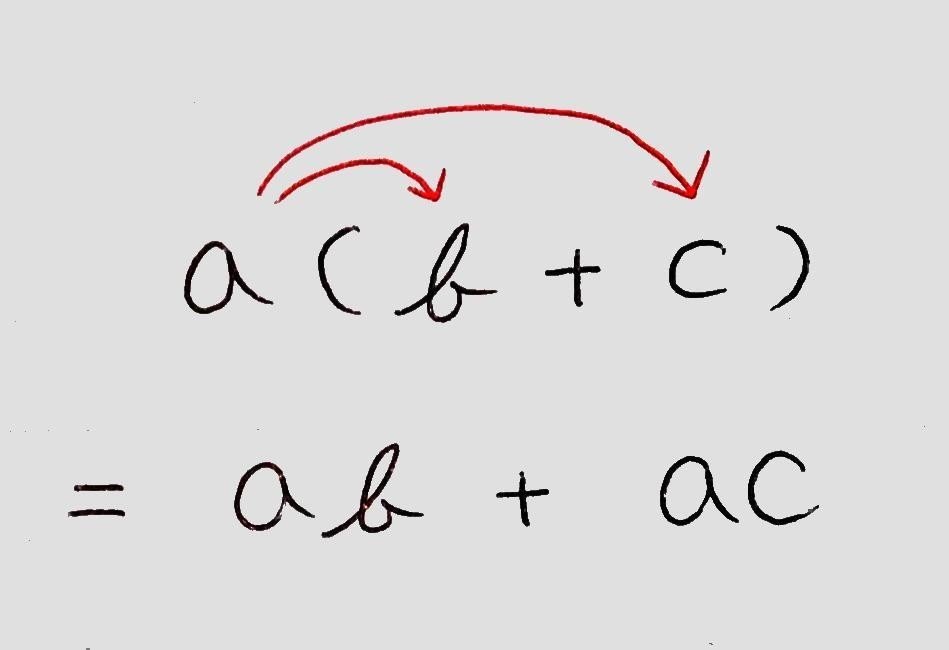
（例題）

　(3a+5b)×2a
=3a×2a+5b×2a
=6a²+10ab

　(7x−2y)×4x
=7x×4x−2y×4x
=28x²−8xy

　−6a(4a+3b)
=(−6a)×4a+(−6a)×3b
=−24a²−18ab

　4x(−3x−8y)
=4x×(−3x)+4x×(−8y)
=−12x²−32xy

　かっこの中の項の数が増えても、計算のやり方は同じです。

（例題）

　5a(5a+9b−3)
=5a×5a+5a×9b+5a×(−3)
=25a²+45ab−15a

　多項式÷単項式の計算も、分配法則を用いて以下の画像のように解くことができます。
※わる数が分数のとき以外。

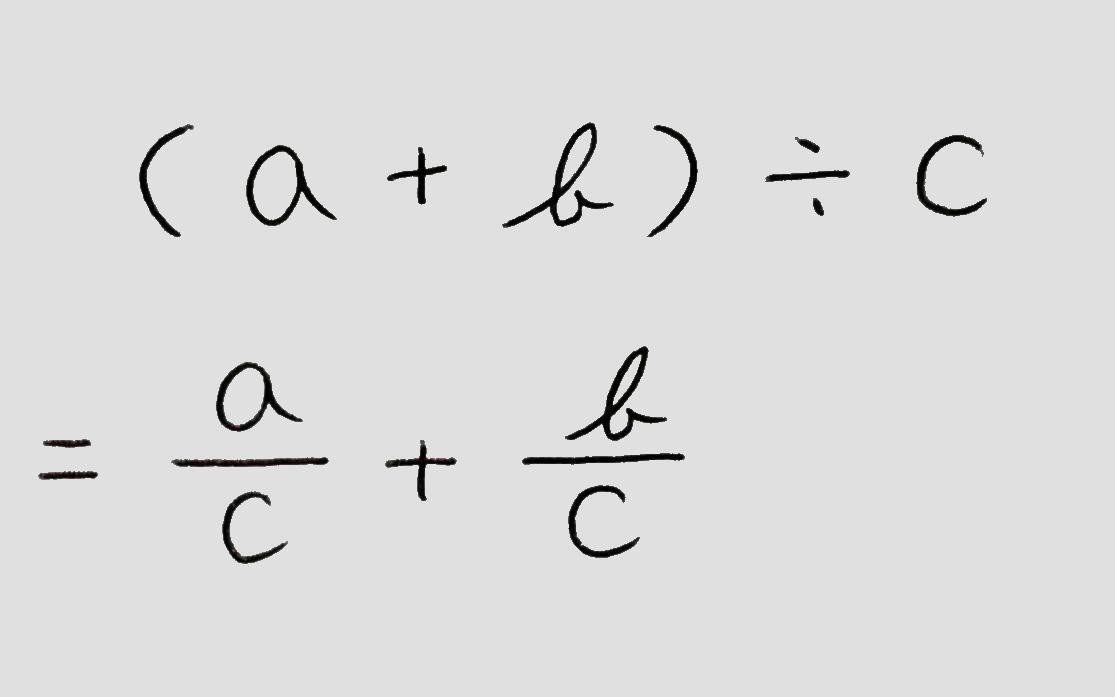
（例題）

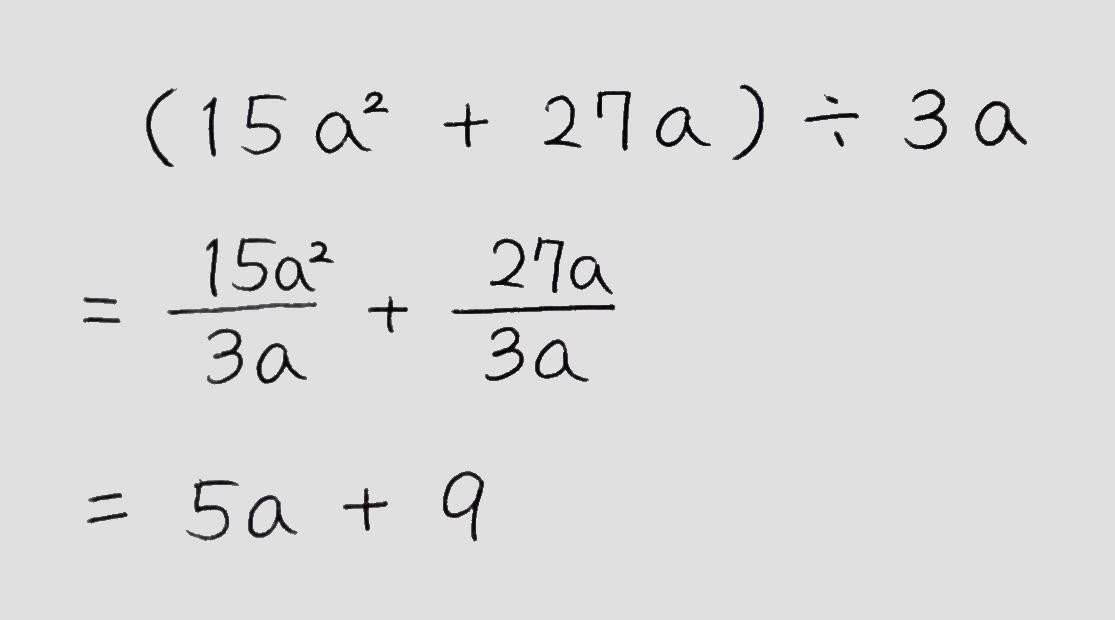
　また、わる数が分数の場合は、以下の例題のように逆数をかける形で計算していきます。
（多項式×単項式と同じ！）

（例題）

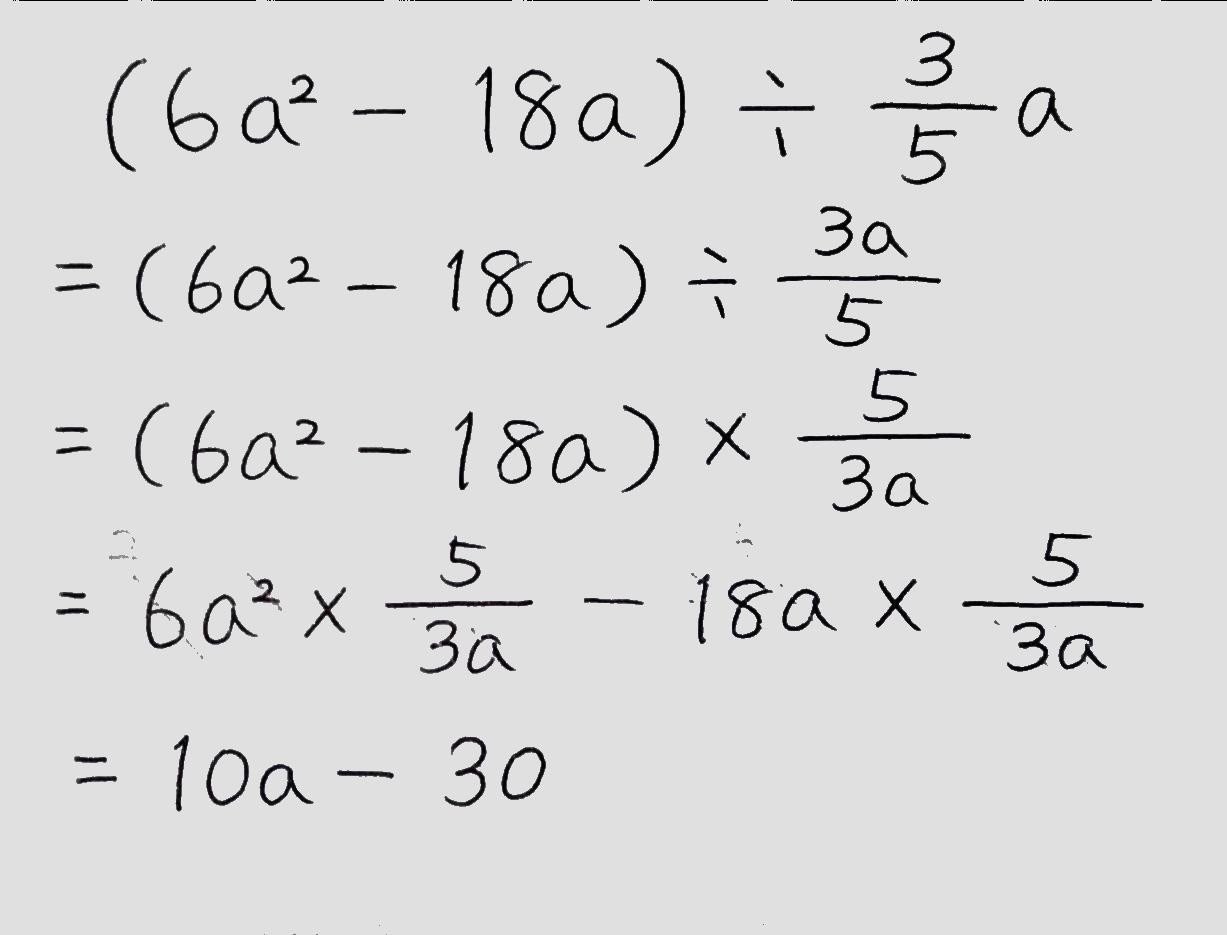
　この項目で確認したような多項式と単項式の計算の考え方は、少し後で紹介する「因数分解」の「共通因数を取り出す」を理解するときにも役立つかと思います！

多項式×多項式

　(a+b)(c+d)　=　ac+ad+bc+bd

　矢印のように分配法則を用いて計算していきます。

　次のような考え方もできます。（c+d）をMとおくと、

　(a+b)(c+d)
=（a+b）M
=aM+bM　　
=a(c+d)+b(c+d)
=ac+ad+bc+bd

※一度置き換えたMをもとの（c+d）に戻すこと、そして、その後の分配法則での計算を忘れないように気をつけましょう。

　計算がごちゃごちゃしやすいので、特に慣れないうちは途中の式を細かく書いて残しながら解いてみると良いでしょう。

（例題）

　(a+4)(b+6)
=ab+6a+4b+24

　(x−2)(y−7)　　(y−7)をMとおく
=(x−2)M
=xM−2M
=x(y−7)−2(y−7)
=xy−7x−2y+14

　展開した式に同類項がある場合は、同類項をまとめることを忘れないように気をつけましょう。

　(a+5)(a+3)
=a²+3a+5a+15
=a²+8a+15

　(4x−2y)(x−9y)　　(x−9y)をMとおく
=(4x−2y)M
=4x×M−2y×M
=4x(x−9y)−2y(x−9y)
=4x²−36xy−2xy+18y²
=4x²−38xy+18y²

　かっこの中の項の数が増えても、やり方は同じです。

（例題）

　(a+b)(2a+b+5)
=2a²+ab+5a+2ab+b²+5b
=2a²+3ab+5a+b²+5b

乗法の公式（展開）

　乗法の公式は4種類あります。全て正確に覚えておきましょう。

※この単元ではもちろん、他の単元（「平方根」や「二次方程式」等）でも活用することになります。

①　(x+a)(x+b)　=　x²+(a+b)x+ab

②　(a+b)²　=　a²+2ab+b²

③　(a−b)²　=　a²−2ab+b²

④　(a+b)(a−b)　=　a²−b²

　①の、(x+a)(x+b)の展開は、分配法則で解くと

　(x+a)(x+b)
=x²+bx+ax+ab
=x²+(a+b)x+ab

となります。公式として覚えておくことで、2行目の計算を省略できるのです。

　②と③は「平方の公式」といいます。それぞれ分配法則で解いてみると

　(a+b)²
=(a+b)(a+b)
=a²+ab+ab+b²
=a²+2ab+b²

　(a−b)²
=(a−b)(a−b)
=a²−ab−ab+b²
=a²−2ab+b²

となります。公式を活用すれば2行目・3行目の計算を省略することができます。

　④は「和と差の積」です。こちらも分配法則で解いてみると

　(a+b)(a−b)
=a²−ab+ab−b²
=a²−b²

となります。公式に当てはめることで2行目の計算を省略することができます。

（具体例）

(x+a)(x+b)の公式

　(x+6)(x+4)
=x²+(6+4)x+6×4
=x²+10x+24

　(x−7)(x−5)
=x²+(−7−5)x+(−7)×(−5)
=x²−12x+35

　(x+4)(x−3)
=x²+(4−3)x+4×(−3)
=x²+x−12

　(x−9)(x+2)
=x²+(−9+2)x+(−9)×2
=x²−7x−18

平方の公式

　(x+5)²
=x²+2×5×x+5²
=x²+10x+25

　(x−3)²
=x²−2×3×x+3²
=x²−6x+9

　(3a+b)²
=(3a)²+2×3a×b+b²
=9a²+6ab+b²

　(−x+4y)²
=(−x)²+2×(−x)×4y+(4y)²
=x²−8xy+16y²

　平方の公式の計算は、「−」の符号の扱いに注意です！

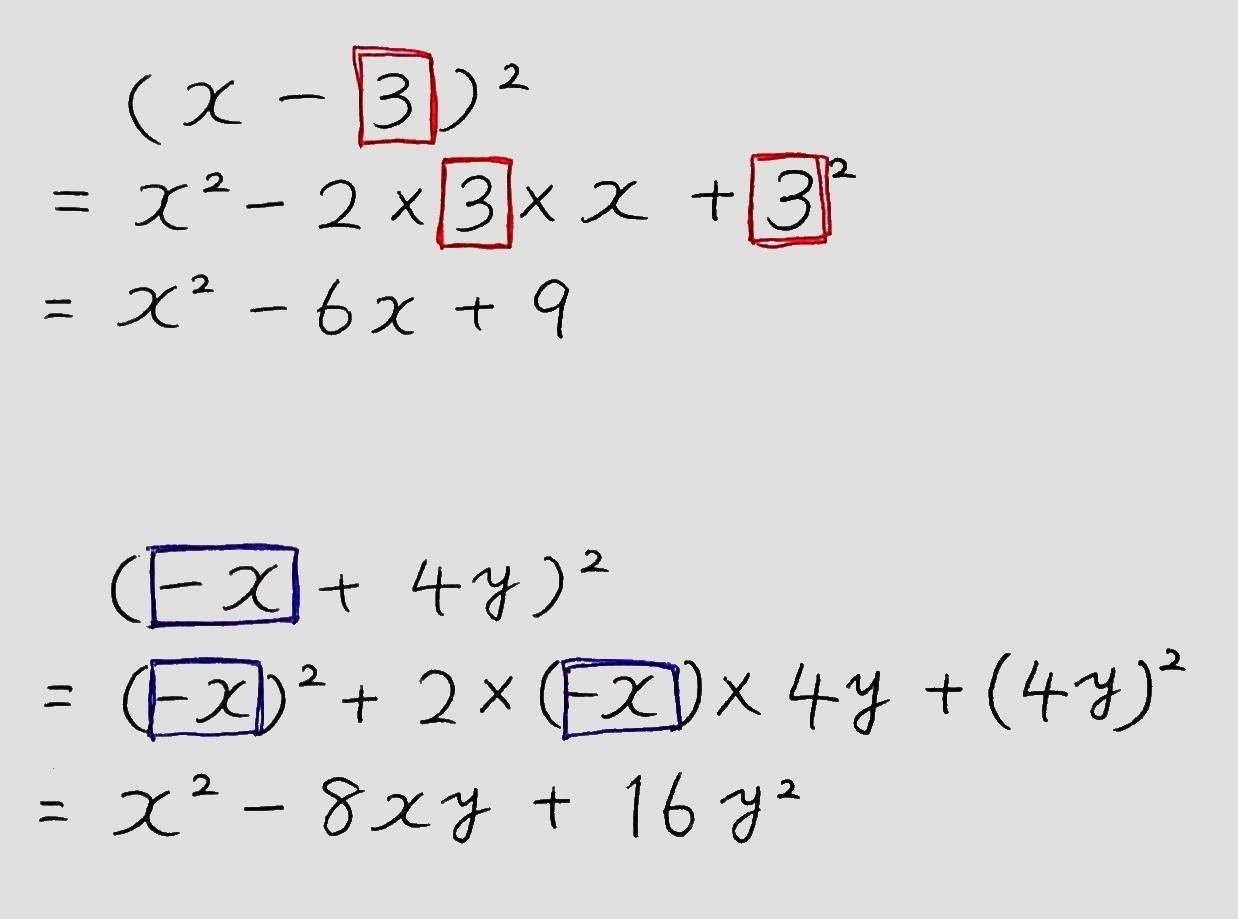
　(a−b)²の計算について、bの部分の項を公式に当てはめるときは、上の画像の赤枠のようにマイナスの符号は含めず、項の部分のみ当てはめてください。符号ごと当てはめると解答がずれてしまいます。

　また、(a−b)²のaの部分の符号がマイナスだった場合は、マイナスも含めて代入します。

（間違い例）

　(x−3)²
=x²−2×(−3)×x+3²
=x²+6x+9　　　←　✕

　(−x+4y)²
=(−x)²+2×x×4y+(4y)²
=x²+8xy+16y²　　←　✕

　「ややこしいな」と感じた人は、分配法則を用いて計算し、答えの符号を確認してみると良いでしょう。

※分配法則で確認してみると……

　(x−3)²
=(x−3)(x−3)
=x²−3x−3x+9
=x²−6x+9

　(−x+4y)²
=(−x+4y)(−x+4y)
=x²−4xy−4xy+16y²
=x²−8xy+16y²

和と差の積

　(x+5)(x−5)
=x²−5²
=x²−25

　(7+a)(7−a)
=7²−a²
=49−a²

　(x+1)(−x+1)
=(1+x)(1−x)
=1²−x²
=1−x²

↑この問題のように、公式に当てはまる形に変形して解くこともあります。

乗法の公式を用いて式を簡単にする

（例題）
(x−5)²+(x+3)(x−3)を簡単にしなさい。

　上のような問題については、まず、乗法の公式を使って「(x−5)²」と「(x+3)(x−3)」をそれぞれ展開します。
※乗法の公式③と④をそれぞれ用います。

　(x−5)²+(x+3)(x−3)
=(x²−10x+25)+(x²−9)

　展開したあとは、同類項をまとめていきましょう。

　(x−5)²+(x+3)(x−3)
=(x²−10x+25)+(x²−9)
=x²−10x+25+x²−9
=2x²−10x+16

　「式を簡単にしなさい」というタイプの問題は、上の例題のようにそれぞれ展開してから同類項をまとめます。
　さらにいくつか例題を見てみましょう。

（例題）

　(x+2)(x−6)−x(x+4)
=(x²−4x−12)−(x²+4x)
=x²−4x−12−x²−4x
=−8x−12

※上の問題は乗法の公式①と分配法則でそれぞれ展開しています。

　「多項式−多項式」の計算は、符号に注意しましょう。上の例題（の途中式2行目）のように、展開した部分を一度かっこでまとめてみるのが良いでしょう。

　−(x+4)²−(x+2)²
=−(x²+8x+16)−(x²+4x+4)
=−x²−8x−16−x²−4x−4
=−2x²−12x−20

※乗法の公式②でそれぞれ展開。

素因数分解

　素因数分解のやり方は2種類あります。解きやすいほうで練習してみると良いでしょう。

（例題）80を素数でどんどん割っていく。

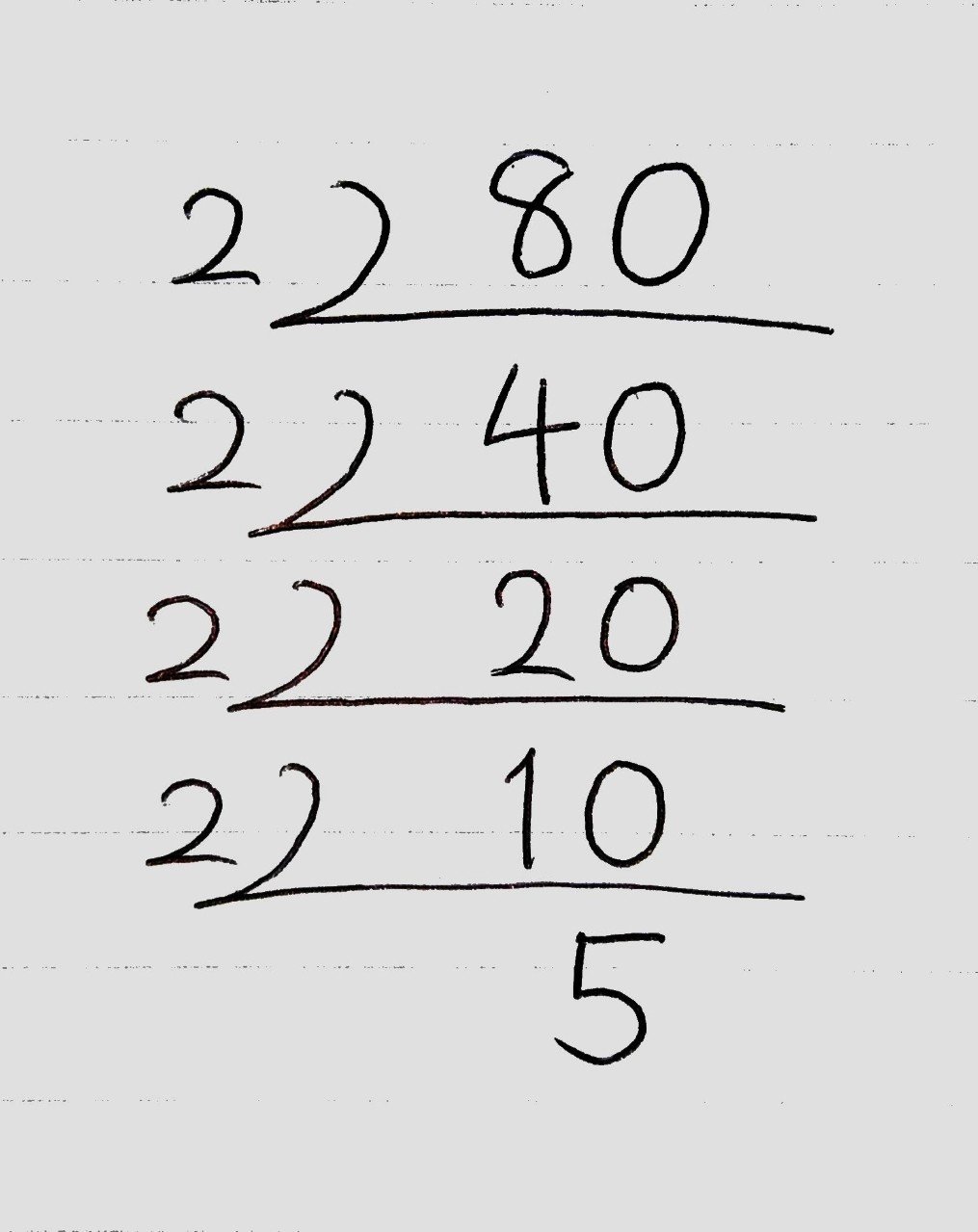
　80を素因数分解すると2×2×2×2×5、つまり2⁴×5になります。

　54を素因数分解すると、

　54 = 2×3×3×3 = 2×3³

　また、下のような方法もあります。

　どういう順番で計算を進めても大丈夫です。

因数分解

　因数分解は展開・分配法則の逆バージョンの計算です。※用語の説明については用語編のnoteをご覧ください。
　因数分解をするときは、まず共通因数を取り出せないか探してみることが大切です。

Ma+Mb=M(a+b)

　上の式でいうと、MaとMbは両方ともMで割ることができます。各項に共通している文字や数字で割ることを「共通因数で取り出す」といいます。

（例題）

　6a²+10ab
=3a×2a+5b×2a　←6a²も10abも2aで割れる！
=2a(3a+5b)

　28x²−8xy
=7x×4x−2y×4x　←28x²も−8xyも4xで割れる！
=4x(7x−2y)

　特に「どのような数で割れるか」を考えていくときに素因数分解が役立ちます。慣れるまでは、それぞれ素因数分解を書いて確認していくのもアリかと。

　項が3つ以上ある場合も同じように共通因数を取り出せないか考えてみましょう。

（例題）

　xa+ya+za　←3つともaで割れる！
=a(x+y+z)

乗法の公式（因数分解）

①　x²+(a+b)x+ab　=　(x+a)(x+b)

②　a²+2ab+b²　=　(a+b)²

③　a²−2ab+b²　=　(a−b)²

④　a²−b²　=　(a+b)(a−b)

　公式④→②・③→①の順に練習していくのが良いと思います。

（具体例）

公式④、和と差の積の因数分解

　x²−25　　
=x²−5²　　
=(x+5)(x−5)

　49a²−16b²
=(7a)²−(4b)²
=(7a+4b)(7a−4b)

　「何かの2乗−何かの2乗」の形になっていたら公式④に当てはめて計算してみましょう。

公式②・③、平方の公式の因数分解

　x²+10x+25
=x²+2×x×5+5²
=(x+5)²

　x²−6x+9
=x²−2×x×3+3²
=(x−3)²

　3つ項があるうち、1つ目の項と3つ目の項が、それぞれ何かの2乗になっていないかチェックしてみましょう。
　例えば、上の例題の「x²+10x+25」であれば、1つ目の項と3つ目の項はそれぞれxと5の2乗になっていますよね。この、xと5をかけて、さらに2倍してみたとき、2つ目の項と同じになれば公式②が使える問題！ということになります。
　「x²−6x+9」のほうも同じ手順で考えることができます。こちらは公式③ですね。
　「何かややこしいな」と感じた人は、後ほど紹介する公式①の因数分解のやり方でチャレンジしてみると良いです！

公式①、x²+(a+b)x+abの因数分解

　公式①の因数分解のポイントは「かけて○、足して○」の手順を覚えることです。どういうことかというと……

（例題）

　x²+10x+24

　まず、3つ目の項に注目。この「+24」の因数をどんどん考えていきます。

1×24
2×12
3×8
4×6
−1×(−24)
−2×(−12)
−3×(−8)
−4×(−6)

※符号に注意。

　次に、2つの因数を足したときに「+10（2つ目の項の係数）」になる組み合わせを探してみましょう。

1+24
2+12
3+8
4+6　　←これ！！
−1+(−24)　
−2+(−12)
−3+(−8)
−4+(−6)

　つまり、この因数分解の問題で使う2数の組み合わせは4と6、ということになります。あとは、
(x+a)(x+b)のaとbの部分に当てはめるだけ。

　x²+10x+24
=x²+(4+6)x+4×6
=(x+4)(x+6)

いろいろな因数分解の問題

①先に共通因数を取り出してから、公式に当てはめるタイプ。

（例題）

　ax²+6ax+9a
=a(x²+6x+9)
=a(x+3)²

　上の例題は、まず共通因数を取り出しています。「ax²」「6ax」「9a」全ての項がaでわれます。
　共通因数を取り出したあと、残った「x²+6x+9」をさらに因数分解します。乗法の公式②が使えますね。

（例題）

　2ax²−50a
=2a(x²−25)
=2a(x+5)(x−5)

　上の問題は、2aが共通因数でした。

　−2でわれたり5でわれたり、aでわれたりxでわれたり……符号・数・文字全てに注目してみる必要があります。
　ある程度慣れが必要な部分もあると思うので、たくさん練習してみると良いでしょう。

②共通な部分を、一度大文字Mに置き換えて考えるタイプ。

（例題）

　(x+y)²+3(x+y)+2

　この問題の場合は、まずx+y=Mと置き換えてみましょう。

　M²+3M+2
=(M+1)(M+2)
=(x+y+1)(x+y+2)

　Mに置き換えたあとは、乗法の公式で因数分解できると思います。上の例題の場合は乗法の公式①が使えますね。
　乗法の公式で因数分解したあとは、必ずMを元の文字式に戻してください。Mのまま終わらないように気をつけましょう。

　もう少し例題を載せます。

（例題）

　(a−b)x−7(a−b)
a−b=Mとおくと、
　(a−b)x−7(a−b)
=Mx−7M
=M(x−7)
=(a−b)(x−7)

　5a(4−b)−b+4
4−b=Mとおくと
　5a(4−b)−b+4
=5a(4−b)+4−b
=5a(4−b)+(4−b)
=5aM+M　　←5aM+1Mと考える
=M(5a+1)
=(4−b)(5a+1)

※問題によっては、上の例題のように項を入れ替えて考える必要があります。

展開・因数分解の考え方を活用した問題（後日追加）