【2023年大学入試数学】 東京大学 理系数学を解いてみた
受験に向けての勉強お疲れ様です。大学入試数学を個人的に研究しているきりんです。今回は東京大学(理系)の数学を解いてみたのでその感想を述べていこうと思います。なお、自分の感じた難易度をつけています。難易度の基準は以下の通りです。
【難易度】
(簡単) A ⬅️ ➡️ E (難しい)
で表していきます。目安としては
Aレベル:正答率80~100%
Bレベル:正答率60~80%
Cレベル:正答率40~60%
Dレベル:正答率10~40%
Eレベル:正答率0~10%(捨て問)
問題






概観
今年の東大理系数学も大問6題構成となっていました。例年より問題文が短くなった気がします。東大では頻出であった整数・数列の問題や複素数平面の問題は出題されず、逆に2013年の出題以来出題されてこなかったベクトルの問題が出題されていたのは驚きでした。傾向が全く読めないのがいかにも東大らしい。
さて、難易度の話に移るのですが、今年は比較的取りやすい問題が1問もなく、大問1つ完答できるだけでだいぶ有利になるでしょう。いつもは解きやすい第1問がそこそこ難しく、本番では解けない人が大多数でしょう。第6問はかなりの難問でした。ただ、第2問〜第6問は(1)だけなら標準レベルなので、部分点狙いで解いていくのが良いでしょう。
設問別解説
ここから設問別にみていきます。
第1問
第1問は積分と極限の問題で、区分求積法がテーマの問題でした。初っ端から(1)で証明問題となっていて、圧倒されてしまう人も多いでしょう。ただ、この問題は(1)が解けなくても(2)は意外と簡単です。気付けた人は(2)だけ解いて部分点を狙うのもいいでしょう。その点も踏まえ、難易度はCレベルです。

(1)からみていきましょう。被積分関数がかなり気持ち悪いですね。絶対値がついてるし、$${\sin}$$の中身が$${x}$$の2乗になっています。もちろんそのまま積分するのはほぼ不可能でしょう。そこで次の原則
被積分関数の気持ち悪い部分を文字で置き換える
に従って解いていくべきでしょう。積分区間の形から絶対値は外せそうなので、$${x}$$の2乗をまとめて$${y}$$かなんかで置き換えてしまいましょう。
(2)に移ると、被積分関数が(1)と同じです。ということは(1)の式を用いて(2)の式を表せそうですね。うまく表してあげると、ちゃんと区分求積法の形になります。はさみうちの原理で極限を求めてあげれば終わりです。答えがあまり綺麗ではなくて少し不安にもなりますが…。
以後、解答です。



第2問
第2問は純粋な確率の問題でした。ここ最近の東大の確率の問題は複雑なルールのものが多かったですが、本問はとても単純な設定になっています。(1)はどの参考書にも載っているような問題ですので確実に正解したいところ。ただ、(2)はそこそこ難しい問題になっています。有名な問題に少し条件を加えるだけで、最難関大学の入試問題に変えてしまうという恐るべき発想ですね。難易度はCレベルです。

(1)は先ほども言った通り、よくある問題なので落とせません。隣り合わないように並べるには
他を並べた後で最後に差し込む
ということをしてあげます。
(2)は赤玉に加え、黒玉も隣り合わないように並べなくてはなりません。ただ、本質は同じでまず白玉を並べます。その後に赤玉か黒玉を片方ずつ差し込んでいき、何通りの並べ方があるか数えていきましょう。場合分けが面倒で式も複雑になるので時間がかかると思います。これまた答えが綺麗ではないので少し不安になります。
以後、解答です。なお、この問題は他にもいろいろな回答が考えられます(同じ色の玉を区別せず考える方法など)。あくまで解答の一例だとしてみてください。



第3問
第3問は座標平面の問題で、数式処理の能力や論理的思考力がかなり要求される問題です。これも(1)はすんなり求めることができると思います。(2)も特にユニークな発想などはいらないですが、変数の置き換えなどで計算がかなり複雑になっていきます。この問題も時間がかかるので行き詰まったら飛ばすのも手です。難易度はDレベルです。

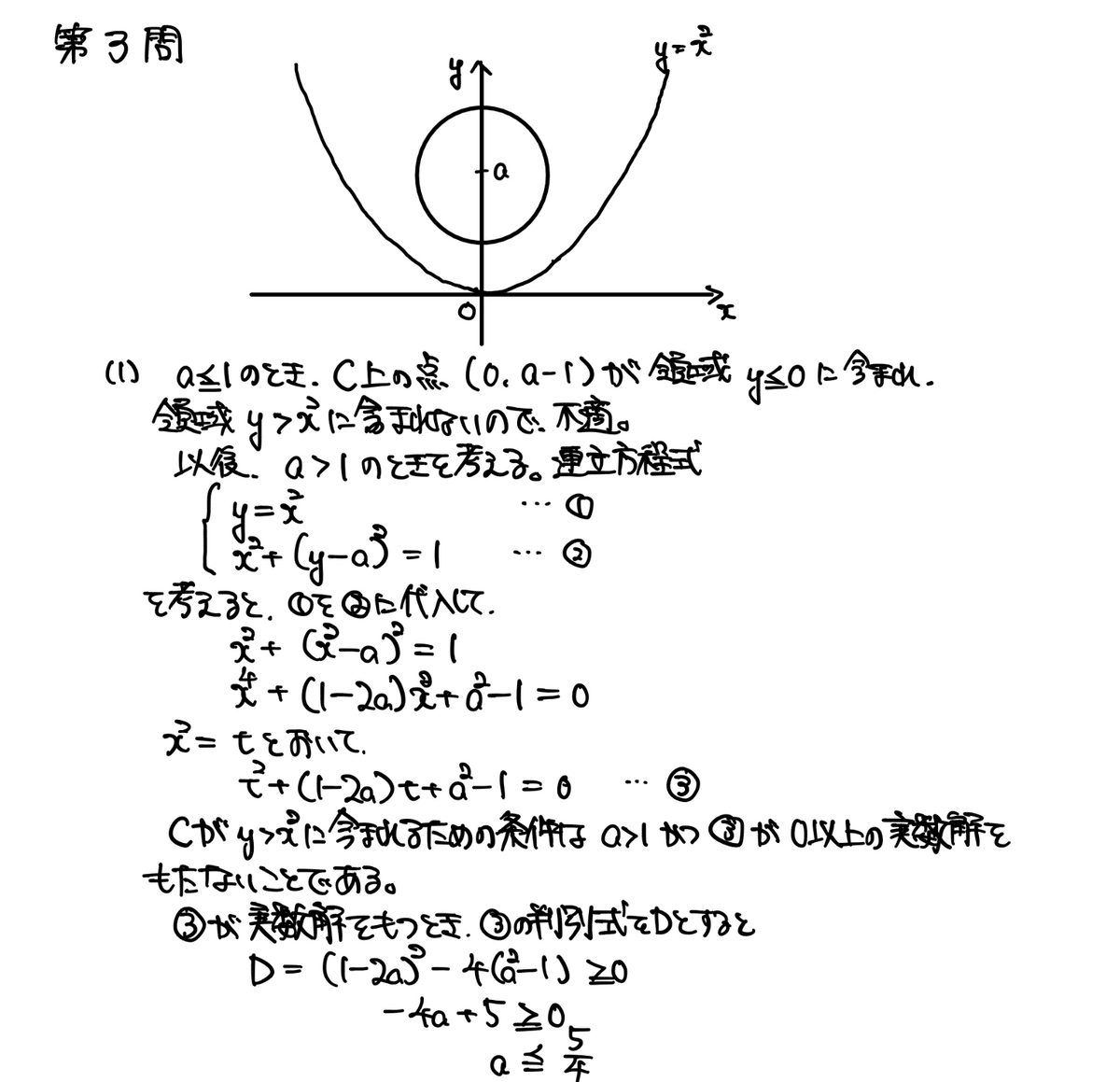
(1)は円が放物線より上側にあるように$${a}$$の範囲を求めてあげればよく、結果的に2次方程式の解の有無の話になります。東大志望者ならスムーズに解けると思います。
問題は(2)です。まず円上の点Pの座標についてですが、点Pの座標を$${(p, q)}$$とおいて計算するのはあまりお勧めできません。円上の点の座標はパラメータ$${\theta}$$を用いてなるべく使う文字を減らしましょう。またこの$${\theta}$$を用いると線分の長さも簡単に表すことができます。問題の条件は言い換えると$${\theta}$$の関数$${L(\theta)}$$が極値をもつことです。これも2次方程式の解の話になります。
以後、解答です。



第4問
第4問は空間ベクトルの問題でした。今年の問題の中ではおそらく最も簡単な問題だと思います。それでも普通に難しいです。(1)と(2)は簡単なので落とせませんが、(3)はこれまた計算量が膨大です。ただ、方針が立ちづらい問題ではないので時間に余裕がある人は完答を目指してもいいかもしれません。難易度はBレベルです。

(1)はPの座標を文字で置いて、内積を計算するだけですので簡単です。
(2)も簡単です。Hについての2つの条件
①直線AB上にある
②ABとOHが垂直
を用いれば係数を決められると思います。
(3)が少し厄介です。要は三角形OHB上を動き回る点と点Qとの距離の最大値・最小値を求めれば良いことになります。空間図形が苦手な人にとっては難しいかと思います。
以後、解答です。


第5問
第5問は多項式の割り算についての問題でした。多項式の問題は東大でも過去に何度も出題されてきましたがどれも難問です。本問は多項式の割り算について扱った問題ですが、整数の合同式のような考え方を用いることになります。あまり見かけないような問題で苦戦した人が多いでしょう。難易度はCレベルです。

(1)から見ていきましょう。ここで余りが等しいことを示すときには、整数の問題でよく使う次の定石を使います。
$${a}$$と$${b}$$は$${n}$$で割った余りが等しい=$${a-b}$$は$${n}$$の倍数
この場合は多項式の問題ですが、やることは同じです。素早く終わらせたいところです。
(2)が本題です。(1)は流石に(2)で使うことになることは予測できます。(2)をうまく使ってあげると$${h(x)^{49}}$$を$${f(x)}$$で割った余りが$${h(x)}$$になるという条件に帰着するはずです。ここでもう一つ定石をあげておきます。
まず、(割られる数)=(割る数)×(商)+(余り)の式を書いてみる
多項式の割り算の問題では必ずこれを行なってください。何か見えてくるはずです。あとはいつも通り$${x}$$に何か値を代入していきます。今回は割る式に$${(x-1)^2}$$がついているので、両辺を微分した式も考える必要があります。
以後、解答です。


第6問
第6問は毎度おなじみ求積問題でした。求積問題は毎年のように出題されていますので、これから東大を受験する方も必ず練習しておく必要があると思います。ところが本問はかなりの難問ですので、本番で解けたという人はまずほとんどいないでしょう。実際自分もかなり苦戦して150分という時間制限内では解けませんでした。難易度はEレベルとしておきます。しかし、(1)だけだったらBレベル程度の問題ですので、(1)は確保しておきたいところです。

(1)は問題文の理解に少し時間がかかると思いますが、少し考えれば立体$${V}$$は、立方体と球の一部を組み合わせた形になっています。立方体の一辺の長さが2であるということだけ気を付けて計算しましょう。
(2)はかなり難しいので、本番ではよっぽど数学の力がある人以外は飛ばして他の問題に移るのがいいと思います。まず、点Nが線分OP上にある、つまり3点O,N,Pが一直線上にあるときは(1)と同じ状況となるので、$${W}$$は$${V}$$を含むということがわかると思います。あとは$${U=W \cap \displaystyle\bar{V}}$$を考えれば良いのですが、点NがSの蓋のふちに存在するときを考えれば良いということを上手く説明する必要があります(実際解答を書くのにかなり苦労しました)。ここまでできればあとは計算するだけです。幸い積分計算はラクそうです。
以後、解答です。





戦略
入試本番でこの問題に出会ったときにどうすればよいか述べていきたいと思います。難易度的には
大問1 (1)やや難 (2)標準
大問2 (1)やや易 (2)標準
大問3 (1)標準 (2)やや難
大問4 (1)易 (2)やや易 (3)標準
大問5 (1)標準 (2)やや難
大問6 (1)標準 (2)難
となっています。こうしてみると部分点の取りやすい問題がかなり多いことがわかります。こういう易しい問題をいかに点数に繋げられるかが合格への鍵となります。また、大問1のように(1)は難しくても(2)は割と解きやすいといったケースがありますので全部の問題に目を通しておくことは忘れないようにしましょう。
まとめ
今年は全体的には若干難化したかなといった印象です。前年とは異なり完答しやすい問題がありませんでした。ここ最近東大数学がかなり難しくなってきている気がします。この傾向は2019年くらいから出てきていて、2014年〜2018年の問題は最近のと比べると結構簡単です。最近の難易度に慣れたい、東大の難しい問題を解きたいという人は1990年代頃の古い問題を解くのをおすすめします。鬼のような問題が並んでいる年もありますので、力がある人は挑戦してみてください。なお、そのうち東大の過去の問題の解説もしていこうと思いますのでよろしければチェックしてみてください。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?