【2024年大学入試数学】 東京大学 理系数学を解いてみた
受験に向けての勉強お疲れ様です。大学入試数学を個人的に研究しているきりんです。今回は東京大学(理系)の数学を解いてみたのでその感想を述べていこうと思います。なお、自分の感じた難易度をつけています。難易度の基準は以下の通りです。
【難易度】
(簡単) A ⬅️ ➡️ E (難しい)
で表していきます。目安としては
Aレベル:正答率80~100%
Bレベル:正答率60~80%
Cレベル:正答率40~60%
Dレベル:正答率10~40%
Eレベル:正答率0~10%(捨て問)
問題


概観
今年の東大理系数学も大問6題構成となっていました。今年は誘導問題なしの問題が2題もあるというセットでした。東大らしい図形・立体の問題が多かったり、半分が微積分の問題であったりと、今年も東大らしさは健全でした。第6問に整数問題を持ってくるのは意外でした(第6問が整数問題なのは2002年以来の22年ぶり)。逆に怖いですね。
難易度についてですが,今年は個人的には易化したと思います。前年までの難問揃いのセットではなくなりました(とはいえ、今年も第6問は難問でした…)。2021年と同じくらいの難易度だと思われるので、合格者の平均点は60点前後になると思われます。参考にしたのは↓の記事です。合格するためには,他の教科を見ていないためあまり強くは言えませんが、最低でも45点は欲しいところです。
難易度レベルは以下の通りです。
第1問 A
第2問 B 〔(1):B (2):A (3):B〕
第3問 D 〔(1):A (2):C (3):D〕
第4問 B 〔(1):B (2):B〕
第5問 C
第6問 E 〔(1):C (2):E〕
設問別解説
ここから設問別にみていきます。
第1問
第1問は領域の問題でした。難易度レベルをAレベルとした通り、絶対に落とせない問題となっています。計算ミスをすると怖いので、ゆっくり時間をかけて確実に得点しましょう。
条件(i)はよいとして、(ii)と(iii)は角度に関する条件です。座標空間を考えているということもあり、ここは内積を使って$${\cos\angle{\text{AOP}}}$$と$${\cos\angle{\text{OAP}}}$$を求めるのが自然です。不等式を両辺2乗する際に少し注意すれば、条件式が簡単に導かれます。
以後、解答です。ちなみに、(ii)の条件だけはPの座標を$${(r\cos\theta,r\sin\theta,0)}$$とおいた方が早いです。


第2問
第2問は定積分の入った関数の最大値・最小値を求めるという問題で、典型問題です。(1)は微分・積分を計算するだけ、(2)は$${\tan\displaystyle\frac{\pi}{8}}$$を計算するだけ、と簡単そうですが、計算量はかなり多いです。難易度はBレベルです。
(1)は場合分けして絶対値を外して、微分するだけです。微分積分の関係式
$${\displaystyle\frac{d}{dx}\int^x_c f(x)dx=f(x)}$$
がわかっていれば、微分はすんなり計算できると思います。$${x}$$がインテグラルの下についているときにマイナスがつくことを注意してください。
(2)は倍角の公式、もしくは半角の公式を使うだけです。(1)が解けた人は確実に得点したいところ。$${\tan\displaystyle\frac{\pi}{8}=\sqrt{2}-1}$$くらいは覚えておいてもいいですね。ただし、解答には導出過程も書きましょう。
(3)は最大値と最小値を求めていきます。最小値は(1)、(2)で求めた通り$${x=\tan\displaystyle\frac{\pi}{8}}$$でとるので、代入して積分計算をしていきます(少し疲れます)。最大値は端点($${x=0,1}$$)でとることは明らかなので、どちらが大きい値なのか調べるために$${f(0)}$$と$${f(1)}$$の両方を計算していきます。どちらも簡単な積分計算で求まります。
以後、解答です。



第3問
第3問は確率漸化式の問題です。どこかの予備校が東大模試で出題しそうな問題です。東大受験生以外の人から見れば、難易度はDレベル級の問題ですが、模試等でこのタイプの問題を何度も解いてきた東大受験生にとってはそこまで難しくない問題であったと思います。確率漸化式の問題のポイントは
全確率の式を忘れない
ことです。
(1)は流石に取ってほしい問題です。いくらか実験してあげることで、とりうる点がどこかわかってくると思います。ここで、$${n}$$が奇数か偶数かでとりうる点が変わってくることに気が付けば完璧です。
(2)は対称性を用いて解答を書いていきたいところですが、言葉だけで説明するのはやや酷なので、漸化式を立ててその式が同じであることを示したり、表を用いて確率が等しいことを示したりしましょう。
(3)では漸化式を解いて確率を求めていきます。Pが$${(2,1)}$$上にあるのは$${n}$$が偶数のときだけであることや、全確率の式$${a_n+c_n+e_n+g_n=1}$$を使って$${a_{2m+2}}$$と$${a_{2m}}$$のみの式に変えてあげます。あとは計算を頑張るだけです。
以後、解答です。(2)の解答には色々な書き方が考えられますし、もっとエレガントに説明する方法もたくさんあると思いますが、ここでは受験生が一番再現しやすそうな解法を選びました。

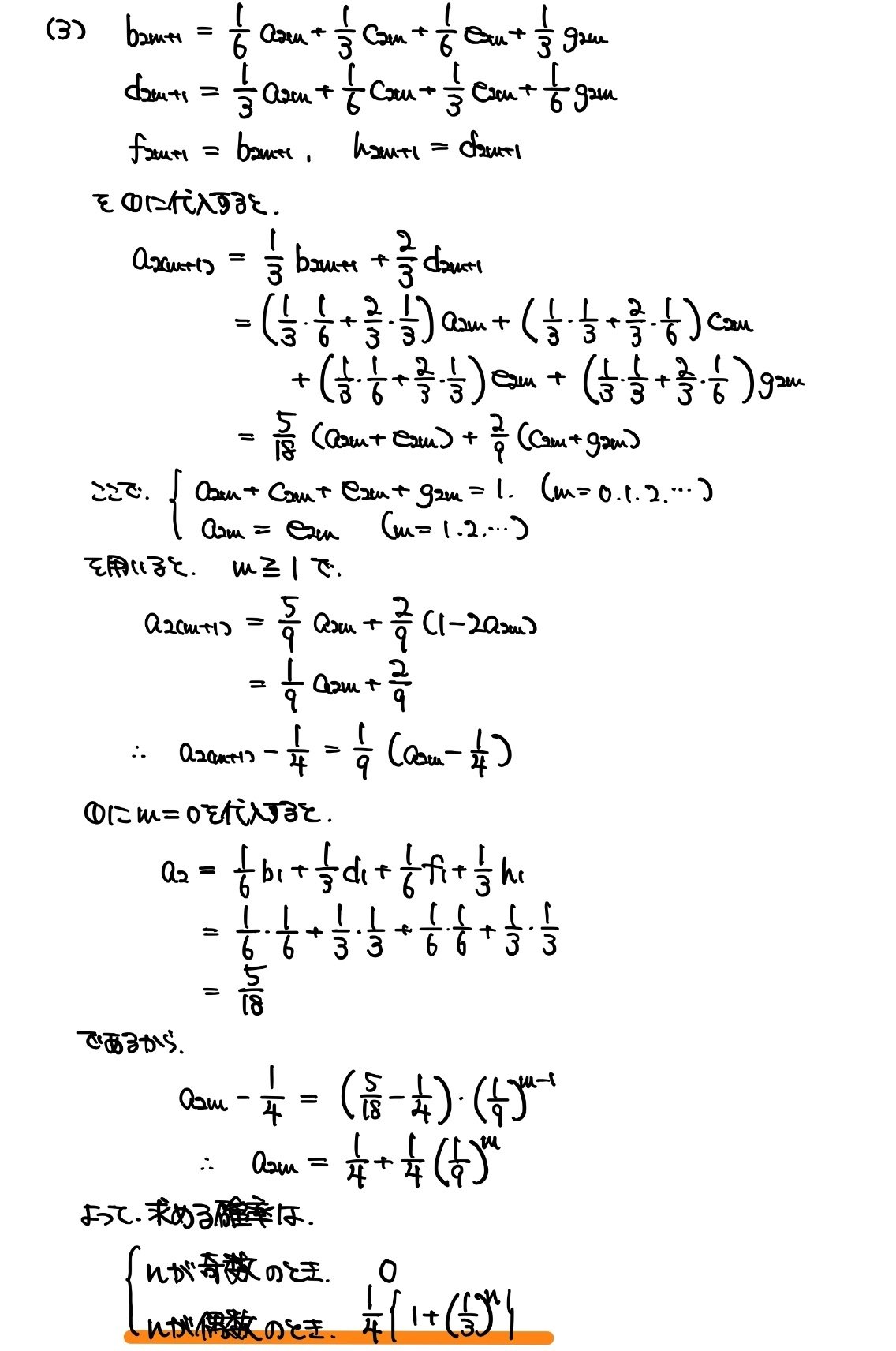
第4問
第4問は図形問題と微分を混ぜた問題でした。とはいえ図形の知識はほぼ要らず、微分計算だけで解けてしまいます。計算量がやや多いため難易度はBレベルです。
(1)は円に関する知識
円の接線と、中心と接点を通る直線は直交する
を用いれば、$${y=f(x)}$$の$${x=t}$$における法線を考え、$${x}$$軸との交点を求めてあげます。あとはひたすら計算です。$${r(t)}$$の計算で6次式が出てきて怖いですが、頑張りましょう。
(2)では円が$${(3,a)}$$を通るような条件を書いてあげると、$${a^2}$$を含んだ$${t}$$についての4次方程式が出てきます(6次方程式じゃなくてよかった…)。この解の個数を考えればよく、
定数は分離する
を用いて解答していきます。
以後、解答です。


第5問
第5問は非常によくあるタイプの求積問題です。積分計算がどうしても煩雑になるため、難易度はCレベルとしましたが、東大受験生であれば方針はすぐに立てたいところです。
回転体の断面を考えますが、原則的には
回転軸に垂直に切る
ことをしていきます。今回は回転軸が$${x}$$軸なので、平面$${x=k}$$で切っていきます。
また、回転体の断面を考えるときのもう一つの原則
回転体は回転させる前に切る
をしてあげないと大変なことになります。回転体の断面は円かドーナツ状の図形になるので、回転させた後の断面を考えてもよくわかりません。
つまり、三角形ABDを$${x=k}$$で切ってあげます。すると線分が出てきますので、あとは点$${(k,0,0)}$$からの距離が最大になる点、最小になる点を考えてあげます。
以後、解答です。


第6問
第6問はまさかの整数問題です。東大は整数問題を第2問や第4問に配置しがちなのですが、例年難問が配置される第6問に置かれてしまうと受験生も私も身構えてしまいます。実際解いてみるとちゃんと難問でした。去年の第6問みたいな無理問ではないので数学が得意な人はチャレンジしてみるのもいいですが、数学の苦手な人は迷わずスキップしましょう。問題文が短くて簡単そう!と思って沼にハマってしまうと大変です。
(1)はよくよく考えれば素数となる必要条件は思いつくと思います。$${f(n)}$$が因数分解できるので、素数となるためには2つの因数のどちらかが±1である必要があります。ただこれは十分条件ではないので、ちゃんと素数であるか確かめなくてはなりません。
問題の(2)です。$${g(n)}$$が定数を2つ含んでいてかなり抽象的な上、ヒント一切なしの難問です。(1)で考えた条件を再び考えることにはなりそうです。色々と式を書いていくと、$${n^2+an+b=1}$$が素数解を持つとき、$${n^2+an+b=-1}$$が素数のマイナス1倍の解を持つことがないということを示せることがわかります。といった風に解答進めていくとなんとか正解に辿り着けます。この問題は、残りの問題が全部解き終わった人向けですね。
以後、解答です。


まとめ
今年は東大数学の歴史の中でも難易度が抑えめな年であったと思います。そういう年こそ計算ミスが怖くなってきます。常日頃から計算ミスや論証ミスに細心の注意を払って勉強していきましょう。どうでもいい話ですが、ここ3年ほど複素数平面の出題がないです。6,7年前ではよく出題されてたのですが。もう出さないつもりなのか、たまたまなのか気になるところです。
ここまで読んでくださりありがとうございます。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?