【AtCoder】緑コーダーがABC288Eの解説やってみた
Hello World! 霧しゃまです!
前回の初投稿記事ではぼちぼち反応を頂けてうれしい限りです。
今日は高度な問題にアタックしたいAtCoder緑前後の方をメインターゲットに、初級者目線での思考過程を紹介してみるテストです!
*数学は専門ではないので、用語や記号の書き方が変なところがあるかもしれません。ご指摘いただけますと幸いです……
今日の問題
今回扱う問題は、2023/02/04(土)に行われたAtCoder Beginner Contest 288のE問題"Wish List"です!
以降、問題のネタバレを含むのでご注意ください!
問題の解釈
まずは問題文の状況をざっくり整理してみましょう。見た目そこそこ難しそうですが、同じ日のD問題よりはどうにかなりそうな印象です(感じ方には個人差があります)
$${N}$$個の番号($${i}$$)がついた商品が1個ずつあります。
各商品に対応する「定価($${A_i}$$)」が与えられます。
商品を買うときは、その時点で残っている商品の中で、買う商品の番号が下から何番目であるかを参照します。
$${j}$$番目の商品を買うときには、定価 + 追加コスト($${C_j}$$)が必要です。
$${M}$$個の「欲しい商品リスト({$${X}$$})」にある商品をすべて買うまでに必要なコストの最小値を求めます。
前提知識
ここからの解説では、下記のような手法が登場します。
貪欲法(実験に使います)
動的計画法(部分和問題やナップザック問題が解ける程度は欲しいです)
セグメント木(後半でちょっとだけ使います)
比較的簡単な要素の組み合わせで解けますが、考察のステップがやや多いので、コンテスト内で完璧に詰めるにはかなり熟練する必要がありそうです(実際、AtCoder Problemsでは黄難度判定です)。
しかしながら、鉄則本あたりで出てくる知識の組み合わせでも高度な問題に食らいつけることを知ることは、緑より上を目指すうえでの第一歩になるのではないかと思っています。一緒に解いてみましょう。
なお、本文ではコードを貼らず図解での解説をしますが、最後に紹介する実際の提出コードはC++で書いています。
忙しい人向けのまとめ
貪欲法ではダメです!!
自分より小さい番号の商品をいくつ買っているかで追加コストの選択肢が決まるので、各商品に「買う」「買わない」の分岐がありそうです
$${dp[i][j]}$$:$${i}$$個目までの商品のうち、$${j}$$個買うときの最小コストとし、$${10^{18}}$$くらいで初期化します
$${i+1}$$番目の商品を買うときは、$${dp[i+1][j+1] = dp[i][j] + (最小コスト)}$$という遷移になります
最小コストを愚直に求めるとTLEになるので、高速化のためにminのセグメント木を使います
欲しい商品リスト内の商品は必ず買うように遷移して、最終的に$${dp[N]}$$のうち最小の値が答えになります
実際に解いてみた
机上で実験してみる(貪欲法)
まずは、問題の性質を把握するために貪欲法でやってみます。
問題を見た瞬間にDPだと直感した方も、余裕があればなぜDPでないといけないのか(なぜ貪欲法では解けないのか)を知るために、この嘘解法を1回以上経験しておくとよいかと思います。

入力例1です。黄色で塗ったところが欲しいものです。
これは「番号の小さいほうから順に、欲しいものを最小コストで買う方法を探す」という貪欲法で正解することができます。
なぜ小さいほうからなのかというと、「自分より小さい番号の、買うと決めた商品の数」がコストの計算に影響するからです。
順を追って見ていきましょう。
まず、3番の商品について考えます。
3より小さい番号の商品で買うと決めた数は0です。
普通に買うと、$${A_3 + C_3 = 10}$$です。
2番の商品を買うと、$${A_3 + A_2 + 2C_2 = 9}$$なので得です。
$${C_1 = 9}$$なので、1番の商品を買うパターンは枝刈りします。
ということで、2番と3番の商品を買うと決めます。
次に5番の商品について考えます。
既に2個の商品を買うと決めているので、追加で商品を買わずに
$${C_5, C_4, C_3}$$のいずれかを選ぶことができます。
最小は$${A_5 + C_5 = 8}$$で、これ未満にはできません。
以上より$${9 + 8 = 17}$$が答えです。

買う順序は意識する必要がありません。選んだ追加コストで支払いができるような順序は必ず存在します。このため「すでに買った数」ではなく、「買うと決めた数」と表現しています。
ざっくり考えると、$${i}$$番の商品を、自分より小さい番号の商品を$${l}$$個買った後に買うと、$${C_{i-l}}$$のコストで買えます。
その時点での「買うと決めた数」が$${l}$$個以上なら実現可能です。
それにしてもやっぱりこの解法は嘘解法です。テストケースのうち4割くらいは通るのですが、それ以上はどうにも無理です。
そもそも、自分より小さい番号の商品を追加で買うときの買い方が指数オーダーなので、全探索ができません(上の方法では見落としがあります)。
また、あるところでは損をしても、のちに得をするようなケースがあります。

上のような状況では、3番だけ見ると$${24}$$が最小ですが、その場合5番を見たときの最小が$${55}$$になり、合計$${79}$$です。
ここで、3番のときに敢えて2番も買うと合計$${29}$$ですが、5番を買うときに$${C_3}$$が選べるようになり、最小$${25}$$になります。合計$${54}$$で、これが最小です。
3番を$${C_3}$$で買うと決めてから5番のときに$${A_2 + C_2 = 15}$$を追加で払うと、合計$${24 + 15 + 25 = 64}$$であり、最小ではありません。
これらのパターンを網羅して考えるために、ここからいよいよ動的計画法を使います。
動的計画法(DP)で考える
ABC288の本番中、霧しゃまは上のような貪欲法を実装して、嘘であることを思い知らされました。そのあたりでタイムアップになってしまったのですが、ほぼ同時に動的計画法に至る気づきを得ました。
ちょっとメタなことを言うと、制約が$${N, M ≤ 5000}$$です。これは、$${O(N^{2})}$$や$${O(NM)}$$、$${O(N^{2} logN)}$$あたりが通るレベルです(この辺の感覚は精進で養うしかないかも)。そして、DPはこのくらいの計算量になります。
貪欲法での実験でもわかった通り、番号の小さいほうから買うか買わないかを決めていけば、追加で商品を買わずに選べる$${C_i}$$の範囲が自然にわかります。これはDPとしてまとまりそうです。
具体的には、"$${dp[i][j]}$$:$${i (i ≤ N)}$$番目までの商品のうち、$${j (j ≤ N)}$$個買うときの最小コスト" とします。
$${A_i, C_i ≤ 10^{9}}$$なので、オーバーフローを防ぐために64bitの整数型で定義します。
最小コストの記録に干渉しないよう、初期値は到達しえないほど大きな値($${10^{18}}$$とか)にしておきます。以下の説明ではとりあえず"INF"とします。
ここは天下り的ですが、問題を観察して、綺麗にまとまるものを探すしかないと思います。DPのパターンはかなり多様なので、どうしてもある程度問題数を経験するまでは、この部分(軸の決め方)に時間が掛かります。
では、入力例1に対する$${dp[i][j]}$$を埋めてみましょう。
まず、$${dp[0][0] = 0}$$は自明です。また、$${j > i}$$になることはありません(i個中i個より多くを買うことはできません)。
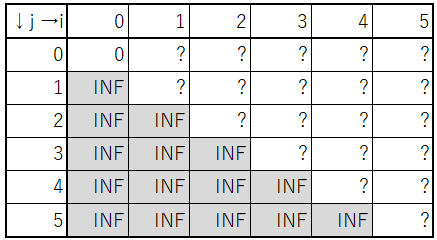
遷移は「配るDP」にします。「次の一手」が明確に規定できるからです。
例えば、$${dp[0][0]}$$の次は、1番を買うか・買わないかです。
買う:$${dp[1][1] = dp[0][0] + A_1 + C_1 = 12}$$
買わない:$${dp[1][0] = dp[0][0]}$$
*実際に遷移するときには、chminなどでその位置の最小値を更新してください
$${dp[1][0]}$$の次は、2番を買うか・買わないかです。上と同様です。
で、$${dp[1][1]}$$の次も2番を買うか・買わないかなのですが、ここで少し違うことをしなければなりません。

具体的には、追加コストを$${C_{i-j}}$$から$${C_{i}}$$の区間で選ぶことになります。この区間における最小値が必要です。遷移はこうなります。
買う:$${dp[2][2] = dp[1][1] + A_2 + \min_{l \in [1, 2]}C_l}$$
買わない:$${dp[2][1] = dp[1][1]}$$ *最小値の更新であることに注意
この区間の最小値の求め方は後程考えます。買わない場合の遷移は同じです。

ここまでの遷移の式を一般化して書くとこんな感じだと思います。
買う:$${dp[i+1][j+1] = dp[i][j] + A_i + \min_{l \in [i-j, i]}C_l}$$
買わない:$${dp[i+1][j] = dp[i][j]}$$
次は3番の商品ですが、問題の制約上、3番は絶対に買わなければなりません。それは、「買わない」の遷移をしないことで表現できます。
欲しいものをsetみたいなものに入れておいて、その番号が欲しいものであるかどうか一発で判定できるようにしておくと良いでしょう。
あとは同じです。5番までやっていきます。

こうすると、$${dp[5][j]}$$のどこかに答えがあります。具体的には、その中の最小値が答えです。$${dp[5][3] = 17}$$です。欲しいもの以外に何を買うかとか、どういった順番で買うかとかはこの数字からはわかりませんが、ともかくも求めたい答えはこれでわかりました。
*「DPの復元」を使えば買うものの一覧がわかり、そこから少し計算すれば買う順番までわかると思います。
追加コストの最小値の求め方
保留していた部分が1つあります。$${C_i}$$の選べる区間の中での最小値です。これは愚直に求めると最悪$${O(N)}$$であり、全体のオーダーが$${O(N^3)}$$に上がってしまうのでダメです。
セグメント木などを用いれば、これを$${O(\logN)}$$に落とせます。全体では$${O(N^{2} \logN)}$$になるので通りそうです。
セグメント木の詳細については優良な解説が他にたくさんありますので、そちらに投げさせてください。
簡単に紹介すると、セグメント木は、配列の区間に対する「合計」「最大・最小」や「GCD」といった演算の結果を二分木構造によって集約するデータ構造です。今回のように配列の様々な区間に対してその演算を行う必要がある場合に有用です。
鉄則本では8.8章です。蟻本にも載っていますが、螺旋本には載っていないようです。ライブラリ化して、モノイド(ざっくり言えば扱う演算の種類)をクラスとして換装できるようにすると便利です。
そしてACへ……
以上の過程を経てできた、霧しゃまの提出コードを晒します。本番中に書いて最初にACを取れたときのものなので、多少の無駄はありますがご愛敬ということで。
こっちはおまけ。貪欲法(嘘解法)を実装したコードの供養です。
ACした感想
紆余曲折がありながらもどうにか自力でACにたどり着いて(累積3敗)、難易度を見て驚きました。ぶっちゃけ、その喜びを共有したい!というのがこの記事を書いた動機です。
AtCoder Problemsに出てくる難易度というのは「そのレートの人の半分がコンテスト中にACできる」という指標なので、時間を掛ければ解ける問題も意外にあるのかもしれません。
AtCoderには「道具の応用」で解ける問題がたくさんある(らしい)ので、考察などのテクニックを磨くことで、難しいアルゴリズムやデータ構造を覚えなくとも、伸びしろを作ることができます。今回のことでそれをなんとなく感じました。
霧しゃまは効率を重視しすぎて、まだ水色以上の問題に全然手を付けていなかったので、良い刺激になりました。
毎日のようにやると疲れますし学習効率も良くありませんが、今後もたまには難しい問題にアタックしたいと思います。そして、気が向いたら今回のように初級者目線の解説を書きに来ます。
そういえば、Twitter(@kiri_comp)も始めたので覗きに来てください!
以上、霧しゃまでした!
追記(2023/3/1)
初心者による背伸びした解説でしたが、予想以上に多くの方に読んでいただいているようでたいへんありがたく思います。
「追加コストの最小値の求め方」の項ですが、公式解説にも書いてあるように、$${O(N^{2})}$$で使用する可能性のあるすべての区間について、追加コストの最小値を前計算することができます。これによってセグメント木を持ち出す必要がなくなります。
実際にやってみました。34行目付近で前計算をしています。
$${C_i}$$の値を、配列$${minC[i][i]}$$に受け取っています。この配列の意味は、"$${minC[L][R]}$$:$${L}$$番目から$${R}$$番目までの追加コストの最小値"です。求め方は$${minC[i][i]}$$を起点に、左側へDPのような感じで遷移させていきます。一部を図示します。
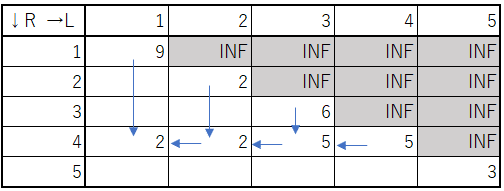
これによって、実行時間を$${logN}$$の分だけ削減できます。メモリの使用量はかなり増大していますが、問題のない範囲です。

どちらのパターンも実装量はほとんど変わりませんが、セグメント木パターンはライブラリを用意していれば、値を詰めるだけで使うことができます。前計算もDPができれば難しくはない(ここだけ抜き出したらC問題レベルだと思います)ので、計算量的に問題ないことを制約などから確認できたら、慣れている方を選ぶのが良いでしょう。
この記事が気に入ったらサポートをしてみませんか?
