【Pythonで統計モデル】SEM4：パス解析（非逐次モデル）

2023年9月25日 11:35

はじめに

こんにちは。株式会社GA technologiesのAI Strategy Centerという研究開発の部署に所属している三田と申します。

現在、私の所属しているData Scienceチームでは構造方程式モデリング（structural equation modeling: SEM）の勉強会を行っており、それに対応する形でメンバーで分担して記事を書いております。これまで次のような記事が出ております：

【Pythonで統計モデル】SEM1：速習・構造方程式モデリング｜福中公輔
 【Pythonで統計モデル】SEM2：母数に関する制約｜福中公輔
 【Pythonで統計モデル】SEM3：パス解析（逐次モデル）｜白圡義泰

本記事はSEM記事の4本目にあたり、パス解析における非逐次モデルを扱っていきます。

この「Pythonで統計モデル」の記事シリーズでは今後も各メンバーが学んだことをそれぞれ記事にしていきます。もしご興味のある方がいらっしゃいましたら、AISCのマガジンのフォローをお願いします！

なお、私はSEMについては全くの初学者になります。もし誤りなどがあればコメントでご教示いただけますと幸いです。

テキスト

本記事では豊田秀樹（2014）『共分散構造分析［Ｒ編］―構造方程式モデリング―』で取り上げられていた事例をPythonを使って再現していきます。分析用のデータは東京図書のホームページからダウンロードできます。

ちなみに、GA technologiesでは福利厚生のひとつに「テックチャージ」という素晴らしい制度があり、書籍の購入費やカンファレンスの参加費などを金額の上限なく（！）会社が負担してくれます。私は今回の勉強会にあたってSEMの本を何冊か購入しており、テックチャージ制度にかなり助けられています。

環境

本記事では次の環境のもとで分析を行っております

OS：official docker image “python:3.10” (WSL2 Ubuntu)
semopy == 2.3.9
pandas == 2.0.3

パス解析（非逐次モデル）

パス解析（path analysis）とは観測変数だけで構成されるモデルであり、複数の独立変数で複数の従属変数を説明するモデルを構築する分析手法です。

パス解析においては変数間の関係性をパス図（path diagram）として描いていきます。

パス解析で構築されるモデルは逐次モデル（recursive model）と非逐次モデル（non-recursive model）の2種類に大別されます。

逐次モデルは単方向の矢印だけをたどって元に戻る変数が1つもないモデルです。逐次モデルについては前回の記事で扱っておりますので詳しくはそちらをご覧ください。

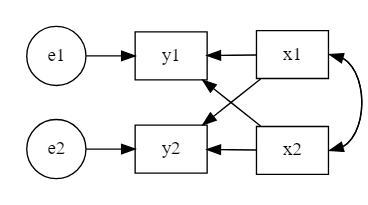
非逐次モデルは単方向の矢印を辿っていったときに起点とした元の変数に戻ることのできる変数が少なくとも1つはあるようなモデルのことです。例えば、次の図のように内生変数同士が互いに影響を与えあっているようなモデルが非逐次モデルです。

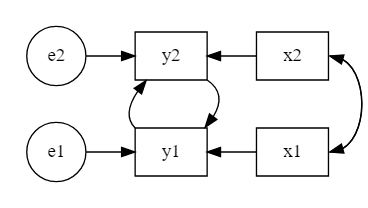
図のように双方向のパスを引く場合、道具的変数（instrumental variable）と呼ばれる変数が必要になります。道具的変数とは、双方向のパスを仮定する2つの変数のうち、一方の変数にだけ直接影響を与え、残りの変数には影響を与えない変数のことです（例えば上の図のx1はy1の道具的変数となります）。

（ちなみに、計量経済学には操作変数（instrumental variable）を用いる操作変数法という分析手法が存在します。私は計量経済学に触れていた人間なのでパス解析を勉強していて「道具的変数って操作変数のことじゃん！」と思いました。関係性が気になったので軽く調べてみたところ、パス解析の考案者であるSewall Wrightと操作変数法の考案者とされるPhilip Wrightは親子であり、操作変数法の初期の文献からパス係数が登場していたりと、初めから繋がりが深い分析手法たちだったようです（Stock & Trebbi 2003）。）

次節からは先述の豊田（2014）のデータとpythonのsemopyパッケージを用いて非逐次モデルを構築していきます。

パッケージとデータの読み込み

fan.csvを使っていきます。これはある野球の球団に対しての応援度合いを表す架空のデータになります。サンプル数は300で、変数は

夫の父の応援度合い $${ x_1 }$$
妻の父の応援度合い $${ x_2 }$$
夫の応援度合い $${ x_3 }$$
妻の応援度合い $${ x_4 }$$

の4変数になります。

import semopy
import pandas as pd

df = pd.read_csv("dat/fan.csv", encoding='shift_jis')
df.tail()

      x1   x2   x3   x4
295  6.8  5.9  4.8  6.2
296  6.8  4.9  4.4  5.0
297  6.8  8.1  4.1  5.7
298  6.9  5.7  6.2  7.9
299  6.9  7.7  4.9  6.2

分析の実行

「夫$${ x_3 }$$と妻$${ x_4 }$$がそれぞれの父からの影響を受けており、夫と妻でも影響を与え合う」というモデルを組んでいきます。

formula = """
x3 ~ x1 + x4
x4 ~ x2 + x3
x1 ~~ x1
x2 ~~ x2
x1 ~~ x2
"""
model = semopy.Model(formula)
model.fit(df)
model.inspect(std_est=True).round(3)

分析結果は `inspect()` で出力することができます。 Est. Stdの列が標準化解になります。

  lval  op rval  Estimate  Est. Std  Std. Err  z-value  p-value
0   x3   ~   x1     0.264     0.299     0.051    5.129    0.000
1   x3   ~   x4     0.071     0.140     0.069    1.035    0.301
2   x4   ~   x2     0.274     0.263     0.051    5.409    0.000
3   x4   ~   x3     0.817     0.417     0.220    3.717    0.000
4   x1  ~~   x1     0.541     1.000     0.044   12.247    0.000
5   x1  ~~   x2     0.249     0.278     0.054    4.645    0.000
6   x2  ~~   x2     1.484     1.000     0.121   12.247    0.000
7   x3  ~~   x3     0.327     0.777     0.047    6.903    0.000
8   x4  ~~   x4     1.045     0.648     0.092   11.340    0.000

豊田（2014）に記載されている結果（Rのlavaanパッケージでの結果）と同様の推定値になっています。

（※formulaに外生変数間の共変関係（x1 ~~ x2）や外生変数の分散（x1 ~~ x1, x2 ~~ x2）を記載しているのは、semopyはRのlavaanパッケージとは異なりこれらのパラメータを明示しないと推定してくれず、自由度や自由度を用いる統計量の推定値がlavaanと一致しなくなるためです。）

パス図の描画

パス図を出してみます。（with句以降はレイアウトを整えるための処理です。`semopy.semplot()` の返り値はgraphvizパッケージのDigraphオブジェクトなのでこのように加工することができます）

g = semopy.semplot(model, "/tmp/img.png", std_ests=True, plot_covs=True)

with g.subgraph() as s:
    s.attr(rank = "same")
    s.node("x1")
    s.node("x2")

with g.subgraph() as s:
    s.attr(rank = "same")
    s.node("x3")
    s.node("x4")

g.attr(rankdir = "RL")    
g.attr(pad = "0.2")
g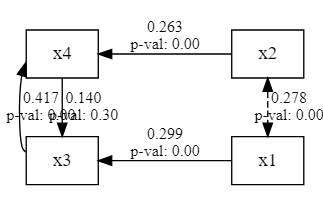

適合度などの指標は次のようになります。

semopy.calc_stats(model).round(3).T

                 Value
DoF              1.000
DoF Baseline     6.000
chi2             1.246
chi2 p-value     0.264
chi2 Baseline  198.714
CFI              0.999
GFI              0.994
AGFI             0.962
NFI              0.994
TLI              0.992
RMSEA            0.029
AIC             17.992
BIC             51.326
LogLik           0.004

なお、semopyのcalc_statsではSRMRを出力してくれません。SRMRの計算方法はPythonで統計モデル（SEM編）第1回の記事で述べておりますので、そちらをご参照ください。

比較用に、Rでlavaanパッケージを用いて分析した場合の各種指標を一部抜粋したものも載せておきます。CFIやUser ModelのTest statistic（カイ2乗統計量）などはsemopyの結果と一致していることがわかります。

Model Test User Model:
                                                      
  Test statistic                                 1.246
  Degrees of freedom                                 1
  P-value (Chi-square)                           0.264

Model Test Baseline Model:

  Test statistic                               174.518
  Degrees of freedom                                 5
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.999
  Tucker-Lewis Index (TLI)                       0.993

一致していないのはBaseline Modelの自由度（Degrees of freedom）です。semopyのDoF Baselineは6であるのに対し、lavaanは5になっています。両者でBaseline model（＝独立モデル：観測変数間にパスを引かないモデル）の自由度の計算ロジックが異なるようです。

lavaanのほうは軽くソースコードを見た限りでは関連する計算が複雑で追いきれませんでした…。しかし、semopyのソースコードはかなり簡潔で、観測変数の数を$${p}$$、推定する母数の数を$${n}$$とすると、

$$
p (p + 1) / 2 - n
$$

という計算をしているようです。これは豊田（2012）や豊田（1998）などでもみられる定義であり、一概にsemopyの誤りとも言えないように思います。

最後に

今回は架空のデータでの分析となりましたが、現実のデータでも変数同士が互いに影響を与えあっている（と想定される）状況は時折発生します。

例えば地域ごとの「警察官の数と犯罪件数」の関係は、単純に相関だけをみていると「警察官を増やすほど犯罪件数は増加する」という結論になりかねません。しかし道具的変数を用いて分析することで「警察官を増やすことによって犯罪件数が減少している」という我々の持つ事前知識に照らしても納得感の高い結果が得られたことが報告されていたりします（Levitt 1997）。

道具的変数は定義からして条件が厳しい変数なので、見つけるのは簡単ではありません。しかし、道具的変数などの分析手法の前提条件がうまく満たされる状況では本手法は極めて強力な手法であると思いますので、機会が来たときに使えるようにしっかり学習しておきたいなと思いました。

今後の流れ

本記事シリーズでは今後もPythonでSEMを実行していきます。次回は王さんが多変量回帰分析を紹介する予定です。ご興味のある方はぜひAISCのマガジンのフォローをお願いします！

参考文献

Levitt, S. D. (1997). Using Electoral Cycles in Police Hiring to Estimate the Effect of Police on Crime. The American Economic Review, 87(3), 270-290.
Stock, J. H., & Trebbi, F. (2003). Retrospectives: Who invented instrumental variable regression?. Journal of Economic Perspectives, 17(3), 177-194.
豊田秀樹. (1998). 共分散構造分析［入門編］. 朝倉書店.
豊田秀樹. (2012). 因子分析入門-R で学ぶデータ解析. 東京図書.
豊田秀樹. (2014). 共分散構造分析 [R 編]. 東京図書.

この記事が気に入ったらサポートをしてみませんか？