図式と操作的確率論による量子論 #3 ～操作的確率論とは～

書籍「図式と操作的確率論による量子論」の紹介記事です。今回は，本書のタイトルにも含まれている「操作的確率論」について説明します。

Kenji Nakahira - 図式

連載の記事一覧：
#1 目的や特徴
#2 図式とは
#3 操作的確率論とは
#4 標準的な量子論の書籍との違い
番外編 ～初学者向け資料～

操作的確率論と古典論・量子論との関係

操作的確率論（Operational Probabilistic Theory）をひと言で述べると，「物体の操作的・確率的なふるまいを具体的な物理法則とは切り離して考える理論」のことです。量子論や量子情報理論の研究者たちの間でしばしば活用されています。古典論（古典確率理論）や量子論や広義量子論（≒古典系を含むような量子論）は，操作的確率論の特別な場合とみなせます。また，本書では，操作的確率論よりも汎用的な理論として「物体の操作的なふるまいのみを考える理論」についても扱い，この理論を操作論とよんでいます。これらの理論の包含関係を示しておきます。

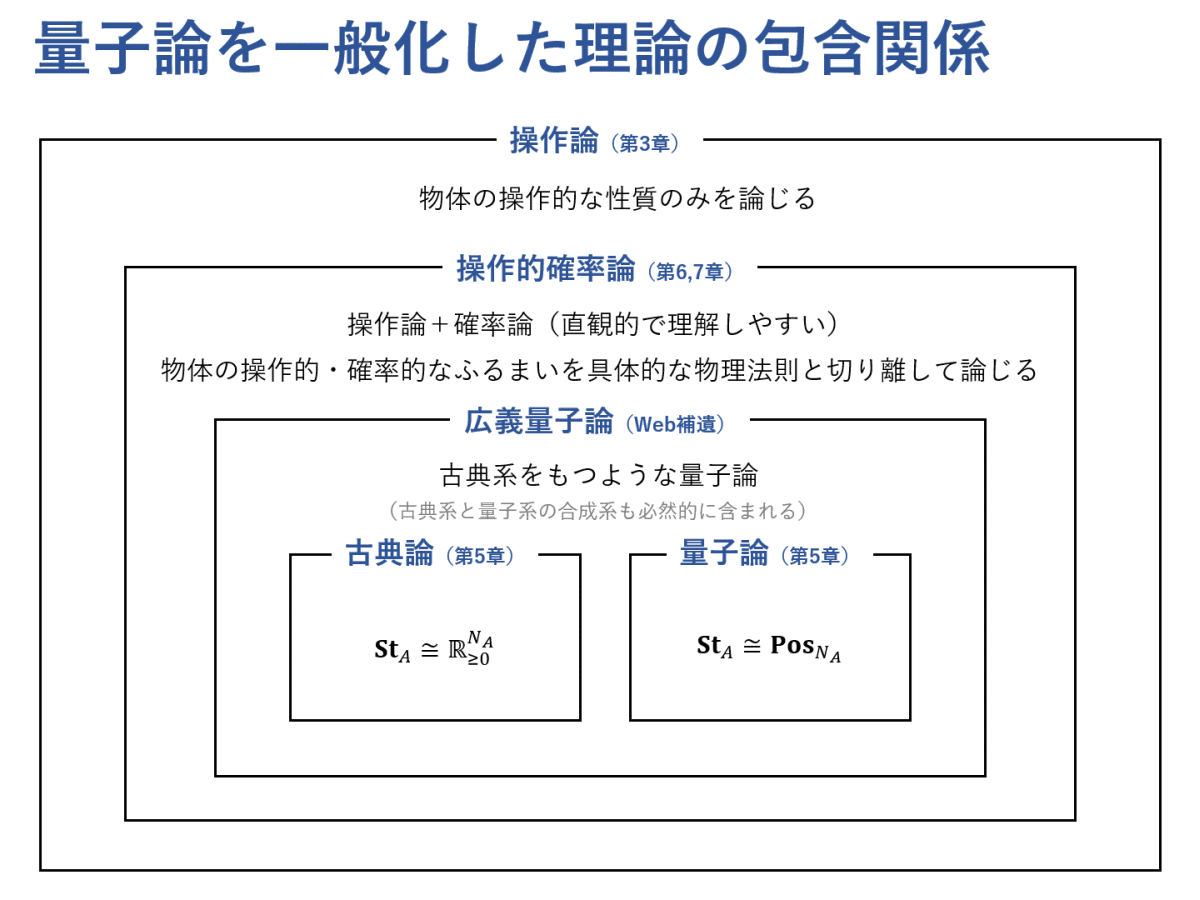
なお，スライド内にある $${ \mathbf{St}_A }$$ は系 $${ A }$$ の状態全体から成る空間を表していますが，ここでは詳細を知らなくても構いません。（「図式で学ぶ量子論」の読者への補足：スライド内にある $${ \mathbf{St}_A \cong \R_{\ge 0}^{N_A} }$$ および $${ \mathbf{St}_A \cong \mathbf{Pos}_{N_A} }$$ は，連載では少し簡略化してそれぞれ $${ \mathbf{St}_n = \R_{\ge 0}^n }$$ および $${ \mathbf{St}_n = \mathbf{Pos}_n }$$ として扱いました。）

操作論とは何か

まず，操作論について説明します。操作論とは，物体の操作的なふるまいを考える理論です。操作論では，物理デバイスのふるまいを抽象化した概念である「プロセス」と，プロセスへの入出力を表す「系」が主役です。プロセスは入力系と出力系をもっています。また，「何もない」ことを表す系（$${ I }$$ と書きます）を導入し，入力系が $${ I }$$ であるプロセスを状態，出力系が $${ I }$$ であるプロセスをエフェクト，入出力系がともに $${ I }$$ であるプロセスをスカラーとよびます。図式では，それぞれ次のように表します。

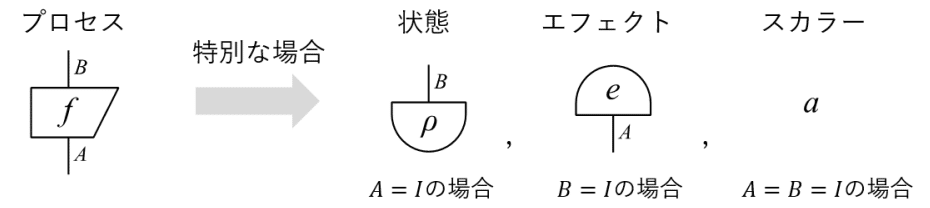
量子状態および量子操作は，それぞれ操作論の状態およびプロセスに対応します。量子測定は，エフェクトの組に対応します。

操作論では，このプロセスについて直列接続と並列接続ができるものとします。

さらに，これらの接続は，直観的に受け入れやすいある規則を満たすものとします。このようにして，プロセスの接続に関する基本的な規則を定めた理論が操作論です。

操作論のすべての規則や具体例については「図式で学ぶ量子論 #1」でも述べていますので，興味のある方はご参照ください。本書では，第3章にて操作論について詳しく説明します。

操作的確率論とは何か

先述のとおり，操作的確率論は物体の操作的・確率的なふるまいを考える理論です。操作論に対して確率の概念を導入した理論ともいえます。

具体的には，スカラーを $${ 0 }$$ 以上の実数と同一視して，これを確率とみなします。また，「放棄エフェクト」とよばれる特別な種類のエフェクトを考えます。系 $${ A }$$ の放棄エフェクトは，次の図式で表します。

そして，次のプロセス（これは入出力系をもたないためスカラーです）を「状態 $${ \rho }$$ を施す確率」とみなします。

また，次のスカラーを「状態 $${ \rho }$$ を準備してプロセス $${ f }$$ を施す結合確率」とみなします。

この図では $${ \rho }$$ と $${ f }$$ が直列接続されていますが，並列接続でも同様に考えます。一方，和が放棄エフェクトになる，つまり

を満たすようなエフェクトの組 $${ \{e_i\}_{i=1}^k }$$ を測定とよびます（和は自然な形で定義できます）。このとき，この測定を行って結果 $${ i }$$ が得られる確率 $${ p_i }$$ は次のスカラーとして表されます。

$${ p_1,\dots,p_k }$$ はスカラーですので $${ 0 }$$ 以上の実数であり，また「$${ \rho }$$ を準備する確率」が $${ 1 }$$ ならば，$${ \sum_{i=1}^k p_i = 1 }$$ を満たすため $${ p_1,\dots,p_k }$$ は確率分布とみなせます。このようにして，スカラーを確率と同一視していくつかの仮定をおくだけで，確率的なふるまいを論じられるようになります。このような理論が操作的確率論です。

量子論では放棄エフェクトを「トレース演算」に対応付けます。また，各系 $${ A }$$ に対してランクとよばれる自然数 $${ N_A }$$ が定まっており，状態 $${ \rho }$$ は $${ N_A }$$ 次半正定値行列で表せます。

操作的確率論では，プロセスを接続するという操作的な考え方に確率の概念を導入しただけですので，直観的に理解できると思います。量子論で現れる複素ヒルベルト空間（これは直観的に理解することが困難であることで悪名高い空間でしょう）は，一般的な操作的確率論では現れません。それにも関わらず，量子論の重要な性質を操作的確率論で説明できることがしばしばあります。このため，操作的確率論は量子論を素直に理解するための強力なツールとして使えます。本書では，第6章にて操作論に対していくつかの要請を導入することで操作的確率論を構築し，第7章にて操作的確率論の基本的な性質を論じます。

操作的確率論は一般確率論とよばれる理論とほぼ同じです。念のため，これらの理論の微妙な違いについて触れておきます。どちらも研究者によって厳密な定義が異なるのですが，操作的確率論とよぶ場合には一般確率論よりも操作的な考え方を重視していることが多いような気がします。また，一般確率論では通常「状態」と「測定」が主役とみなされるのに対し，操作的確率論では「プロセス」が主役であることが多いです。本書でも，操作論と同様にプロセスを主役として扱います。

操作的確率論を用いることの利点

操作的確率論を用いることの主な利点は，以下の三つです。

1. 量子論がもついくつかの本質的な性質を素直に理解できる。

2. とくに物理や数学を専門としない人にとって理解しやすい。

3. 直観的な言葉で書かれた要請を用いて量子論の数学的構造を導ける。

詳しくは，本書の1.1.2項で説明しています。3.については第1回目の記事で述べましたので，1.と2.について説明します。

1.については，一般的には不思議と思われているような量子論の性質のうち，操作的確率論で説明できるものが少なくありません。操作的確率論を習得すると，このような性質が直観的に理解できるようになると思います。量子論の性質を，操作的確率論で説明できるものと説明できないものに分類できるようになれば，量子論を深く理解できるようになることでしょう。

次の図は，操作的確率論に基づいて量子論の性質を理解する方法をイメージ化したものです。

この図は，各性質がどの理論で成り立つかという観点で包含関係を表したものです。たとえば，この図の「操作的確率論」と書かれた楕円の内部の点は，すべての操作的確率論で成り立つような性質を表しています。操作的確率論で成り立つ性質は，古典論と量子論でも成り立ちます。私たちは，馴染みのある古典論に基づいて量子論を理解しようとしがちです。しかし，古典論と量子論には多くの相違点がありますので，この方法ではなかなかうまくいきません。とくに，古典論では成り立つけれど量子論では成り立たないような性質（たとえば，「すべての状態は分離可能である」や「異なる純粋状態は完全に識別できる」といった性質）を先入観としてもっていると，量子論の理解を妨げることになると思います。つまり，古典論で成り立つ性質を当たり前として考えてしまうと，量子論はそれらの性質を満たさない場合があるため不思議だと思えてしまいます。これに対し，本書では操作的確率論を考える，つまり古典論でも量子論でも成り立つようなより基礎的な性質を考えることによって，このような先入観を排除しつつ量子論の性質を調べるというアプローチをとります。操作的確率論を考えることは，「古典論で成り立つ性質のうち真に基本的な性質とは何か？」を考え直すことであるといえそうです。

2.については，本書ではニュートン力学や解析力学などの物理の知識は不要ですし，高度な数学の知識も前提としません。この主な理由の一つが操作的確率論に基づいているためといえます。なお，量子論の数学的構造を理解するためには完全正値写像（CP写像）に関する知識が必要ですが，これについては本書の第4章で詳しく説明します。