複雑そうだけど使えると簡単になる

　一見難しそうに見えるものも、実はそれを使った方が簡単であるという事があります。

　例えばワインオープナー。

　一見複雑な歯車機構があって、初めて見たときは、どういう風に使えばいいのか戸惑う人もいると思います。単にコルクを抜く事を考えれば、

これで十分です。しかし、これで抜くには力加減の調整が必要ですし、多少コツも要ります。

　そこで、最初見せた複雑そうなものは、使い方さえわかれば誰でも簡単にコルクをきれいに抜く事が出来ます。

　電気回路における「複素数」も、まさに

「一見複雑そうに見えるけど、使えるようにさえなればとても簡単に回路計算ができるようになる」

というものです。

　てなわけで、今回は電気回路で複素数を使う利点について、簡単にご紹介したいと思います。関連記事としては、「虚数」について以下でご紹介していますので、ご参考にして頂けたらと思います。

●数直線で考える

　複素数の前に、改めて虚数について確認します。

　虚数とは、

「２乗してマイナスになる数」として、虚数単位を

j^2 = -1

と「定義」します。

　ちなみに、虚数は英語で

imaginary number（想像上の数）

ということで、数学では "i" を使うのですが、電気では電流を表す記号と混同しないように、"j" を使います。

「何でこんな実在しない数を～」

という意見はとりあえず置いといて、今回は、

「これが何を意味して何に使えるのか」

という立場で考えていきたいと思います。

　では、改めて

"-1" 倍する

ことを視覚的に捉えてみましょう。「数直線」で考えると分かりやすいです（下図）。

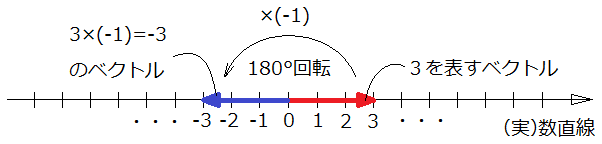
　例えば、"3" という実数を数直線上で表すと、上図のように

 "0" から右向きに、3目盛分の長さの「ベクトル」

になります。

　これに、"-1" をかけてみます。すると、

3×(-1) = -3

は、"0" の左側にありますので、

 "0" から左向きに、3目盛分の長さのベクトル

になります。

　つまり、

"-1” を掛けたことで、ベクトルが 180° 回転している

ことになります。

●虚数は平面をつくる

　それでは、虚数 "j" はどうでしょうか。

j^2 = -1

を、

「"j" を２回掛けると 180° 回転する」

と翻訳してみましょう。すると、下図のように考えることが出来ます。

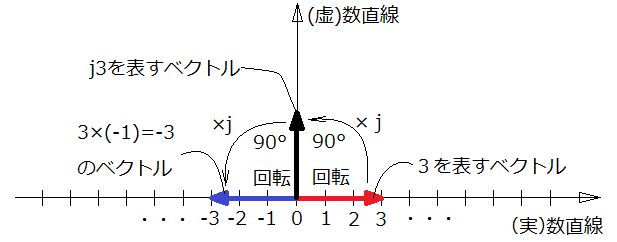
　すなわち、

「"j" を掛けると（"-1" の半分で） 90° 回転する」

と解釈できます。尚、回転方向は、左回転（反時計回り）にしています。これは、約束事として考えてください。

　そうすると、実数とは 90° 違えた縦方向の数直線がそこに現れます。その結果、実数だけの時はヨコ向きの直線軸だけだったのが、虚数を考える事でタテの軸も出現します。

　という事は、

複素数 = 実数 （"j" がつかない）+ 虚数（"j" がつく）

という定義があるので、

「複素数はヨコとタテの軸で平面を張る」

という事になります（下図）。

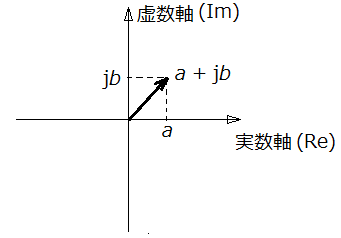
　これを、「複素数平面（ガウス平面）」と呼びます。

　ヨコとタテの軸は、それぞれ

「実数軸」「虚数軸」

と呼び、それぞれ

"Real number" "Imaginary number"

から、

"Re" "Im"

と軸に表示します。

●複素数には向き（角度）がある

　実数は、数直線上でのベクトルの長さと、その向きが「＋かーか」の違いしかありませんでした。しかし、複素数は平面上のベクトルですから、360° どこにも向けられます。

　つまり、複素数は「長さ」と「角度（向き）」を持っている事になります。

　この、

｢角度を持つ｣

のが、複素数の肝になります。例えば、

1 + j√3

という複素数は、

Re（x方向）が "1"

Im（y方向）が "√3"

ですね。これは、下図のような｢直角三角形｣を描くことができて、

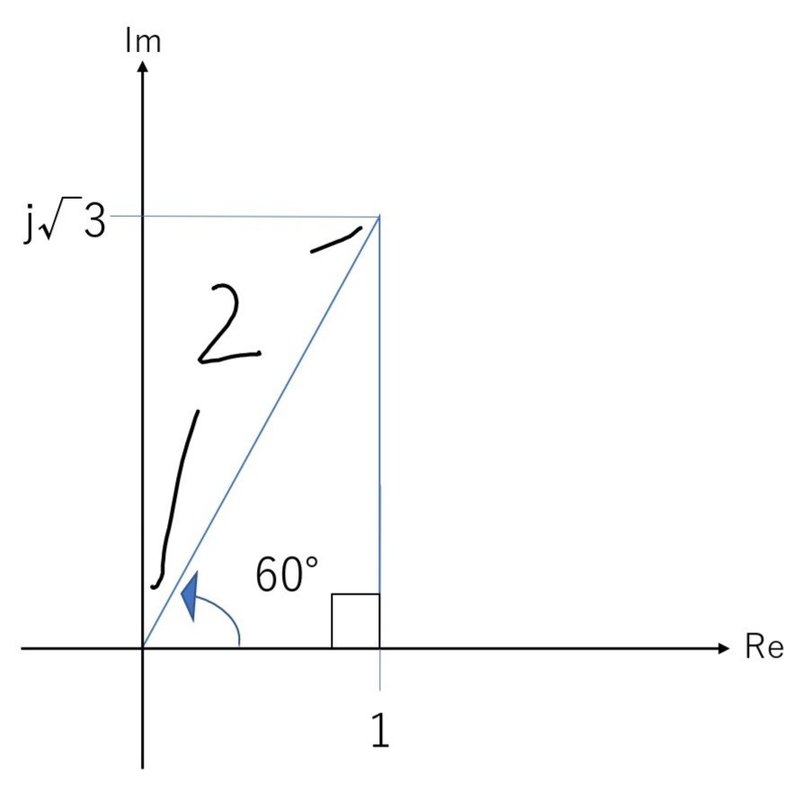
このベクトルの｢Re軸｣との角度は 60°

とわかります。

　もっとも、見てわかるように図を描いただけで、本来は｢三角関数｣を使って、

tan 60° = √3/1 = √3

なので、

tan の逆関数 "arctan" （または "tan-1"）

を使えば、

arctan √3 = 60°

と図を描かなくても、関数電卓などを使って求められます。

　この、

Re軸とベクトルのなす角度を｢偏角｣

と言います。

　ちなみに、

ベクトルの「長さ」、すなわち複素数の「大きさ」

は｢三平方の定理｣より、

|1 + j√3| = √{1^2 + (√3)^2} = √(1 + 3) = 2

と求まります。

●「直交座標」と「極座標」

　ここで、

「複素数の表し方」

について考えてみます。

　先程見てきたように、複素数は

「2つのパラメータ」

を持っています。そして、複素数を表すパラメータには、

①「実数項」と「虚数項」
②「大きさ」と「偏角」

という、二種類の組が考えられます。これらについて、

①で表した形式を「直交形式」
②で表した形式を「極形式」

と呼んでいます（下図）。

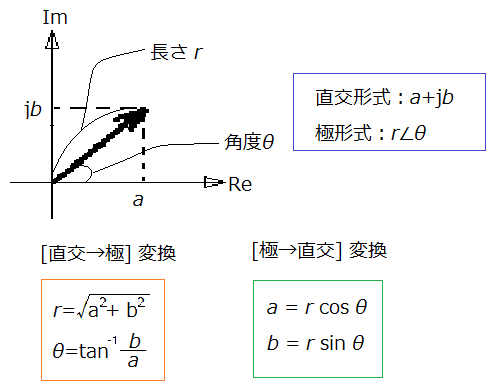
　「直交形式」は、

ベクトルの「足し算」「引き算」

を考えるのに、

「実数同士」「虚数同士」

それぞれ計算すればよいので都合がいいものになります。

　一方、この「極形式」は、

ベクトルの「掛け算」「割り算」を考えるのに非常に都合がいい

のです。何故なら、

A∠α × B∠β

という掛け算は、

AB∠(α+β)

という風に、

「大きさ」同士は「掛け算」（"AB"）

「偏角」同士は「足し算」（α+β）

になるからです。

（理由は、次回「オイラーの公式」を簡単にご紹介します。）

　そして、これが交流回路の計算をとても簡単にします。

●実際に計算してみる

　それでは、以下の交流回路の電源から流れる電流の大きさと、その位相を計算してみましょう。

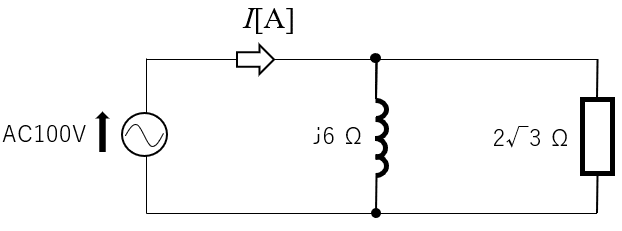
　交流電圧の実行値が 100V の電源に、6Ω のコイルと 2√3 Ω の抵抗が並列に接続されています。

　複素数を使わないやり方であれば、

①コイルの電流 IL = 100/6 = 50/3 A

②抵抗の電流 IR = 100/2√3 = 50/√3 = 50√3/3 A

　コイルの電流は、電圧よりも 90° 遅れるので、IL と IR を合成して（下図）、

③I = √{(50/3)^2 + (50√3/3)^2} = (50/3)√{1+(√3)^2} = 100/3 A

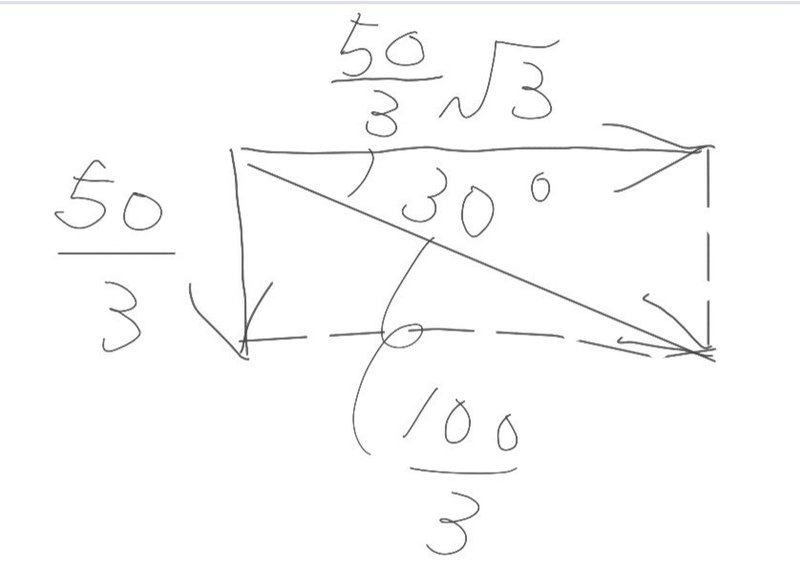
　このように、図を描いて初めて、

電流の大きさが 100/3 Aであること

と、

位相が 30° 遅れであること

がわかります。

　ここで、複素数を使って計算してみます。

　コイルのリアクタンスは、虚数で

j6 Ω

とします。（理由は次回説明します。）

　コイルの電流は、虚数で表すと、

①IL = 100/j6 = 50/j3

ここで、

1/j = j / (j × j) = - j

として、

IL = - j50/3 A

となります。

　1/j = - j

となるのは、

j を掛けると 90° 回転する

ので、

j で割れば - 90° 回転する

と考えても良いでしょう。

②抵抗の電流 IR = 50√3/3 A

でしたので、

③IR + IL = 50√3/3 - j50/3 A

と「複素電流」が出てきます。

　この大きさは、先程の計算と同様に、

I = √{(50√3/3)^2 + (50/3)^2} = 100/3

偏角は、

φ = arctan {(- 50/3)/(50√3/3)} = arctan (- 1/√3) = - 30°

と、図を描かずに計算だけで求めることが出来ます。

●実際はもっと複雑

　この回路は単純なので、複素数の有り難みがあまり実感できないと思いますが、実際の回路はもっと複雑です。とても三角形を描いて解析などしていられません。

　何より、計算だけで処理できれば、コンピュータで自動的に解析出来ます。そのために、この複素数は、とても強力なツールになるのです。

　次回は、オイラーの公式による指数表示と、コイルとコンデンサの｢複素リアクタンス｣について考えてみます。