大数の法則について

今回は大数の法則と中心極限定理について深掘りしていきたいと思います。

まずどっちがどっちか説明できますか。多分ごちゃごちゃになっているかもしれません。（自分もそうだった）

大雑把に説明すると次のようになります。

・大数の法則：試行回数nが大きいほど標本平均は母平均に近づく。
・中心極限定理：母集団分布が何であれ、試行回数nが大きくなるほど標本の平均・分散は正規分布に近づく。

ではまず大数の法則から見ていきます。

・大数の法則

今回はコイン投げをして表が出る確率というテーマを通して大数の法則が成り立つのか確認していきます。
表がでる確率をpを、裏が出る確率を1ーpとします。（つまり0.5, 0.5ということになる。）まず今回は試行回数を10回とします。10回中n回表が出る時の関数を次のようにセットします。（基礎的なCやPに関しては割愛します。）

また表が出た時を1、裏が出た時を0として10回コイン投げを行った時の表の確率変数の和をrとします。（なので全部足したらr＝10となる）また総試行回数nで割ったr/nを相対頻度とします。

今回をコイン投げは二項分布に従うとして、さらに進む前に二項分布における期待値と分散について紹介します。二項分布における期待値と分散は次のように表されます。

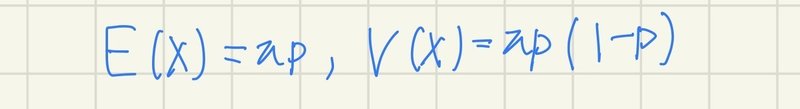
ピンと来ない方のために具体例を挙げます。2枚のくじがあります。あたりとハズレの確率はそれぞれ0.5（1/2）ですね。枚数は2枚なので当たりを引く期待値（ここでは平均と考えてください）は0.5*2で1ということがわかります。二項分布の期待値は直感的に理解しやすいと思います。

では実際に投げてコインを投げてみます。
仮に10回投げて全部表だったとします。今の時点だと時点だと確率は100％ですね。次にさらに10回投げてみます。結果としてそのうち半分が表だとします。今の時点での表が出る確率は15/20です。さらに10回ずつ試行回数を増やしていきます。そうすると20/30, 25/40, 30/50.,......55/100, .... 505/1000となります。これを全て小数で表してみましょう。サンプル数が大きくなればなるほど確率が真の確率（0.5）に収束しています。これを確率の収束と言います。

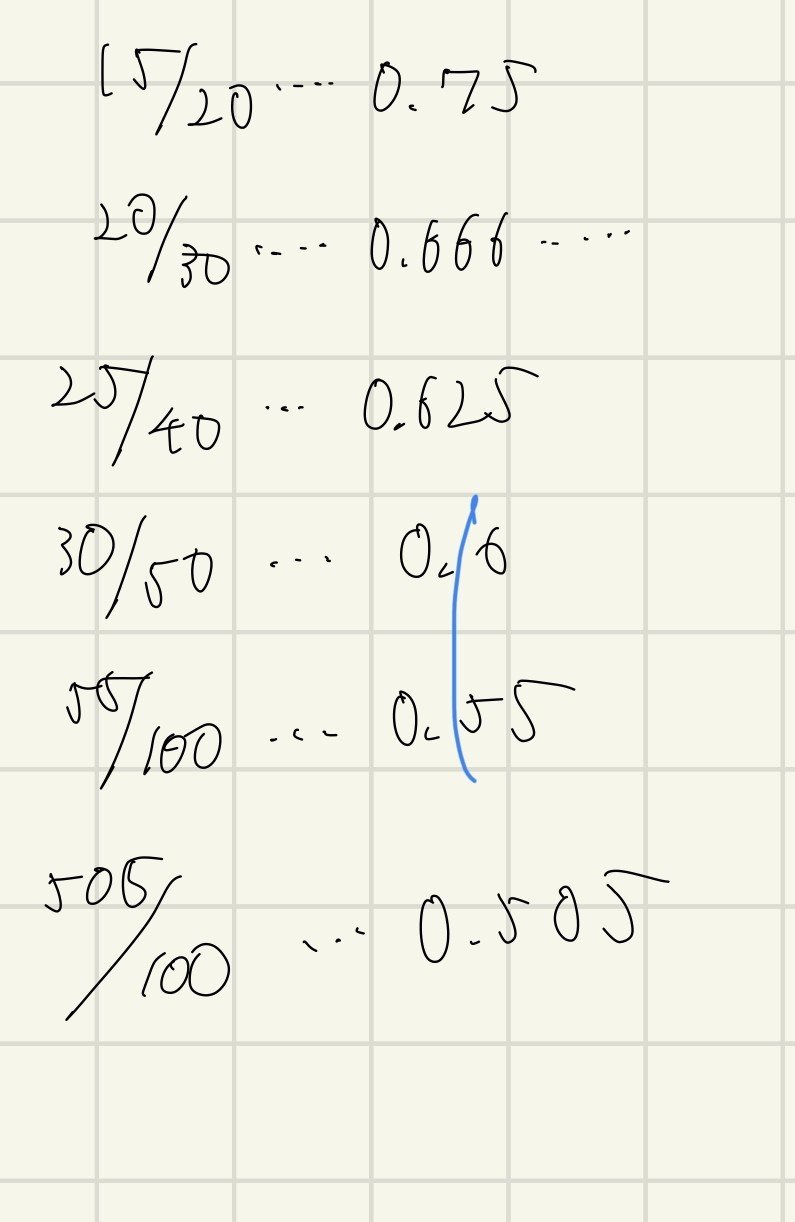
ちょっと説明に困ったので次の動画の説明を参考にしました。

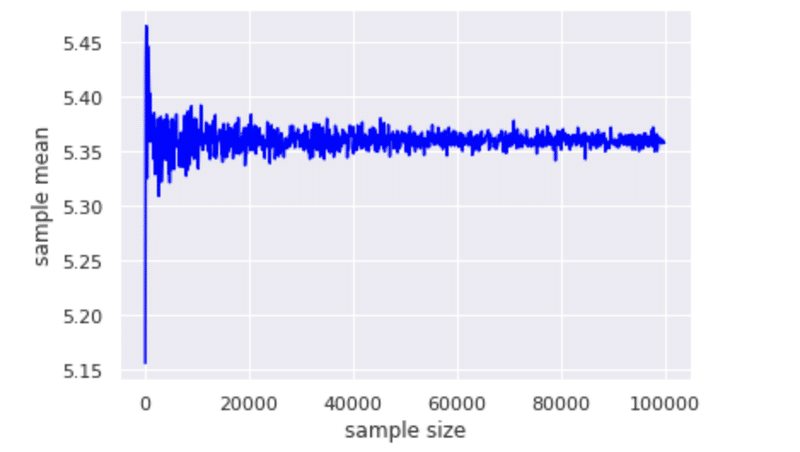
以前の記事で実際にシミュレーションしてみました。真の平均は5.36なのですが、サンプルが大きくなるほど真の平均に近づいていると思います。