
【テニプリ】テニプリを科学的に検証してみた
かつてテニプリを愛した友人に捧ぐ
テニヌ、それはテニスを超えたなにか

作成していて、きぬた歯科デザインが秀逸だと気がついた
みなさん、科学は好きですか?
昔話から始めさせてほしい。興味のない方は「テニプリを科学的に検証してみた」まで飛ばしていただいて構わない。
私がテニプリを見始めたのは2023年の5月ごろからだ。最初に映画リョーマ!その次にアニメから入った。その時非常に疲れていたからか、なぜか新テニから見始めた。感想としてはテニヌというか超次元テニス。
ブラックホールを出したり、一人でダブルスをやったり、なんか球が光ってたり…。現実では中々ありえなそうである。特にブラックホール。どうやるんだろう。
みなさん、テニプリは好きですね?
私はそのような現実離れしているテニスに心を癒やされた。しかし、そうでない人もいた。元物理学徒の友人だ。テニプリ(と推し)をかつて愛していた友人は新テニを見ていないという。なぜかと聞くと「物理学徒としてはブラックホールは許容出来なかった」と言われてしまった。
私も一時期物理学徒だったので、わからなくはない。ただ、本当に勿体ない!勿論多少現実から反れることもあるけれども、そこも面白い。さらにストーリーも大変面白く、キャラも相変わらず魅力的である。私の推したちは今日も素晴らしく輝いている。推し達、いつもありがとう。これからも貢がせてもらう。
そこで、友人のモチベーションを上げるため、テニプリの超次元的な現象を科学的に考察する。例を挙げると徳川のブラックホールは現実では出せるのか?無理だとしたらあの現象は他で説明できるか?など。一人では圧倒的に力不足なので専攻分野が違う友人を集め、テニプリ内の現象をチームを組んで科学的に検証することを試みた。
また、今回テニプリ内で起こった現象を否定するつもりは一切ない!テニプリ内で起こった現象はテニプリ内では真実である。ただ我々3次元側の住民の科学で解説できるかということを目指した。ただし、ここで記述したことは間違えている可能性が大いにあるので、あまり参考にしないでいただきたい。
検証方法
検証会に参加メンバーは3名。履修分野はそれぞれ物理(半分)、数学、機械工学だった。物理がメインなのに物理担当が貧弱すぎる。これではいけない。そのため審査の代わりとして(?)物理学で修士号を取得した他3名の優秀な友人達に確認してもらった。みんな本当にいつもありがとう。
因みに怪しいな、という方は一応筆者のプロフィールを雑に書いたので参照してください。

最初はカラオケの合間に検証を行おうと思ったが、全力で歌ったり筋トレしたり(主に日吉の曲)踊ったり(主にキミパ)するため、疲れてしまう。そのため自宅で検証した。なお、テニラビのAPが回復したら考察よりそちらを優先するというルールも設けた。
では早速始めよう。
定義や注意事項
今回、頻繁に真空での光速が出てくるため(テニスの試合でなんで?)先に記述する。このブログでは真空での光速を$${c}$$として、その値は
$${c=3.0×10^8}$$ m/s
とする。これは1秒間に地球を約7周半する速度である。
また、注意事項が二つ。
一つは新テニの領域はアニメで確認したということだ。無印は全巻持っているが、新テニは持っていない。だいぶ前に34巻まで速読したが、ちょっと内容に自信がない。そのため、新テニはアニメをベースにした。
二つ目は、難易度だ。なるべくわかりやすくしたつもりだが、ちょっと大学レベルのところもあるかもしれない。特に補足などは説明を省いている部分が多く、理系でなければ難しいと思われる。難しかったら飛ばしていただいて構わない。長いので飛ばしながら雰囲気で読んでください。補足は横棒で挟んでおきましたので補足はほとんど飛ばしてください。
テニプリを科学的に検証してみた
忙しい人のためのまとめ
下記に今回検証した結果を簡素に記述する。この結果からやはりテニプリで起こる現象は科学的に考えると中々再現することが難しく、代替できないものもある。また、ブラックホールは現実での再現は不可能であると結論付けた。

1人でダブルス!?
始めると言ったが、素晴らしい例を紹介するので一旦待っていただきたい。
空想科学研究所をご存じだろうか。漫画やアニメ、ゲームなどの現象を真面目に科学で考える研究所である。空想科学読本は小学生の時に見た方も多いのではないだろうか。今回検証したきっかけも空想科学研究所に影響されている。
なんとそれを確認すると菊丸さんの1人ダブルスがあるではないか。柳田氏が解説しているのでリンクを見てほしいが、忙しい人のために結論だけ記述する。
1人ダブルスをやるために菊丸さんは時速720kmで動く必要がある。これは、長太郎のネオスカッドサーブの約3.5倍だ。新幹線はおろかリニアモーターカーよりも速い。さすが菊丸さん。これでスタミナ切れしないとすると相当トレーニングを頑張ったんだろう。試合に参加しなかった誰かのために。
多分理論だけで考えると菊丸さんは一人でD(ダブルス)をやるよりも、天才に死角はナシ!だからS(シングルス)!という感じがする。しかし、そうしない。なぜか?言うまでもない。菊丸さんが本当に必要としているのは大石だということだ。
めちゃくちゃ語りたいところだが、本論からそれるので他の誰かに任せてここまでにしておく。他の同志の方、よろしくお願いします(結局自分でやりました)。
もちろん空想科学研究所のように深く正しく考察することは難しいが、このように検証することを目指した。今度こそ始めよう。
映画リョーマ!でのタイムスリップ
まずはリョーマ!で起こったタイムスリップについて記述する。
「リョーマ! The Prince of Tennis 新生劇場版テニスの王子様」という大変ファンタスティックな映画がある。見ていない方は是非見てほしい。できれば応援上映がやっている時はそちらで見てほしい。強火オタクのお兄様お姉様が場を盛り上げてくれるはずだ。

リョーマ!では最初の方にタイムスリップのようなことが起こる。なんと、現代からリョーマの父南次郎の現役時代にタイムスリップするのである。
タイムスリップが起こった時の現象については下記に示す。
1.リョーマが打ったテニスボールに謎の人物(一応伏せる)が打ったボールに当たる
2.ボールが粒子レベルでばらばらになる
3.周りすべてが粒子レベルでばらばらになり宇宙が見える(???)
4.過去の同じ場所に戻る(南次郎のポスターがあったため二人は過去と判断した)
といった具合だ。
まず、過去にタイムスリップしたような描写だったが、そもそも過去にタイムスリップすることは現実で可能かどうかを考えよう。結論から言うと無理そうである。理由は、理論上すべての物質の速度は(真空中の)光速を超えることができないからである*1。
因みに、論文をチェックしていないが過去に行けるという記事もある。しかし、どちらにしろ過去には干渉できないらしいので、リョーマの父南次郎の八百長試合中止はできないだろう。
では過去に戻ったような描写は何だったのか?我々は下記の仮説を立てた。
「世界が再構築され、過去に戻ったように錯覚した」
現代の世界から過去に戻ったように見えるシーンをもう一度振り返ろう。そこには一瞬にして粒子的にばらばらになり宇宙が映っている。これは世界が再構築されたことを表しているのではないか?
一旦整理しよう。ボールがぶつかる前の世界線、ぶつかった後の世界線、南次郎の試合終了後にボールがぶつかった世界線をそれぞれα・β・γとする。世界線α・β・γはそれぞれ一直線上にある過去と現代のように見え関わりがあると思われるが、実際は再構築してできた世界である可能性が高い。
しかし、1回バラバラになったものを再構築して、しかも似たような世界にすることは無理である。そもそも現実ではテニスボールをぶつけて世界をバラバラにすることももちろん難しい。
一応世界が崩壊することの仮説の1つとして考えられるのは偽の真空を想定した真空崩壊*2だろうか。こちらも仮説になってしまうので、絶対起こるりうるものではない。そのきっかけになったのがテニスボールの衝突だとしたらすごすぎる。
なんにしてもリョーマが戻ってきた(?)似たような世界では、八百長試合ではなくなっていたようで何よりだ。
*1これは特殊相対論による時間の遅れの式からわかる。動いている$${B}$$さんと静止している$${A}$$さんの時間と動いている速度をそれぞれ$${t_B ,V_B ,t_A ,V_A }$$とするとBさんの時間は
$$
t_B=\sqrt{1-{(V_B/c)}^2 } t_A
$$
となる。もし、$${c < V_B}$$であるとするならば、√の中身はマイナスになる。つまり$${B}$$さんの時間は虚数となってしまう。これは時間換算できないと思われる。
追記:特殊相対論とエントロピー
副査Rから「虚数になるから光速を超えないというのがなんか気持ち悪い」とのことだったので、別案を教えてもらった。
別案の内容は「相対論を考慮した合成則と質量とエネルギーの等価性の式より光速を超えないことの証明」である。完全に相対論なので大学レベルである。マニアックな人だけ読んでください。私も選択科目になってから相対論や量子力学から逃げていたので履修していなかった。
まず相対論版合成則から。詳しくは下記リンクを見てほしいが、特殊相対論的な3次元速度$${U}$$の合成則は下記に示される。
$$
U\equiv \frac{V+W}{1+\frac{VW}{c^2}}
$$
ここで、$${V,W\leqq c}$$とすると、どう頑張っても$${U}$$は光速以上になることはない。$${V,W> c}$$だとしても質量とエネルギーの等価性の式(乾のアルバムにありましたね!)より、エネルギーを$${E}$$とすると、
$$
E=(\frac{1}{\sqrt{1-(\frac{V}{c})^2}})mc^2\\
\therefore (1-(\frac{V}{c})^2)E^2 =(mc^2)^2\\
(V≠c)
$$
上記式より、もし$${V> c}$$であったとするならば、左辺の括弧内はマイナスになる。そのため、$${E}$$は虚数になり、虚数の質量やエネルギーをもつことになる。これはありえないため、光速を超えることはない。$${W}$$も同様である。Q.E.D.
更に副査Rから時間自体を過去に戻すとなると宇宙のエントロピーを減少させることができればできるかもしれないと意見をもらった。宇宙を孤立系と考え、宇宙の外からエネルギーを与えてエントロピーを減少させるようにすべてのものを並び替えるとのこと。確かに宇宙の外にエネルギーを行き来させられる神がいるならこれが一番現実的かもしれない。まあすべて現実的ではないのだが…。
*2真空崩壊について簡単に補足する。
量子論で言う真空は基本的に最低エネルギーの状態のことである。相転移を繰り返してきた我々の宇宙は、エネルギーの極小点なだけであり実は真空周りに落ち着いておらず(偽の真空)、真の真空が別に存在する可能性がある。
もしわれわれの宇宙が偽の真空であったとすると何かのきっかけで、真の真空に相転移する可能性がある。そうすると膨大なエネルギーを開放し、世界が終焉する。
つまり可能性としてはテニスボールが相転移のトリガーになったかもしれないということである(ない)。
参考リンク:https://www.jstage.jst.go.jp/article/butsuri/74/3/74_128/_pdf
光る球(デストラクション)
新テニスの王子様で多く登場した光る打球(デストラクション)である。ラケットのちょうど真ん中のスーパースイートスポットに当たると光るらしい。打たれた球は壁も崩れるくらいの危険な威力を持ち、それをリョーマも修行していた。特徴としては黄色やオレンジのような暖色系の色をして光る。

壁が崩れるくらいの威力でありテニスによる入院は後を絶えないと思われる
そもそも現実で打球が光ることはあるのだろうか。電飾などを付けずにそのまま光るというのは中々難しい。一応知っている範囲で3つ仮説を立てた。
①チェレンコフ光による発光
②圧力変化により球が燃えた
③ナトリウムランプと同じ現象が起きた
・チェレンコフ光による発光

最初に思いついたのはチェレンコフ光である。正直これしか思いつかなかった。面目ない。多分もっといい案はあると思われる。
チェレンコフ光とは物質(媒質)内を運動する荷電粒子が、その媒質中における光速を超える時、衝撃波として放出される光であり、基本的に青く発光する。光を超えることあるの?と思った方も多いかと思われる。実は光速の定義は真空中が前提であり、屈折率の関係上ガラスや水の中だと速度は遅くなる。一応式を下記に示す。媒質中の光の速度をc',媒質の屈折率を$${n}$$とすると、$${c'=c/n}$$となる。
しかし、チェレンコフ光の定義的にアウトな部分が多い。まあ一応続けよう。
実は空気中の屈折率は1.0003程度であるため、ほぼ真空と大差ない。そのため光の速度はほとんど下がらない。
光を出す際にまずは空気中の光の速さを超える打球を打たないといけない。とても難しいし、それに伴い、色々な問題も出てくる。さらに、そもそもテニスボールは大した電荷をもたないため、結局光速を超えても無理である。残念。
できたとしてもチェレンコフ光は可視光範囲で青色の光を多く含むため、ドップラー効果*などを使用しないと黄色に光るようにはならない。しかし、実際にリョーマが使用する際に、どの角度から見ても黄色い光になっているので、その選択肢はなさそうだ。
*ドップラー効果について簡素に説明する。救急車で例えると、近づくときより遠ざかるときのほうが低温に聞こえるだろう。それは見かけ上の音の波長が大きくなったからである。今回の例では青色の光より暖色系の光のほうが高い波長のためである。それを利用してボールから遠ざかることによって、暖色系の光に見える!としたかった…。因みにチェレンコフ光を暖色系に光って見えるようにするにはどうしたらいいか(テニスボールとは言っていない)という質問に対し、副査Rから提案頂いた意見である。ありがとう。
・圧力変化により球が燃えた
宇宙船が大気圧に突入する時、燃える現象を知っているだろうか。あれは大気圏に突入するとき、空気が圧縮されて起こる。あの現象に近いと球が燃えて光るのではないかと考えた。
黄色い光を出す炎の温度は3500度である。打ち返す前にボールは燃え尽きてしまう。いや、表面だけ激しく燃えて中心は保つボールかもしれない(無理)。続けよう。
状態方程式*より、燃える圧力の計算はできると思う。しかし、テニスコートは空気に関して開放系であり、空気は無限にある。そのためボールとネットの摩擦でコートを燃やすことができても圧力で発火することは難しいかもしれない。
*状態方程式は圧力、体積、物質量、温度、気体定数をそれぞれ$${P,V,n,R,T}$$とすると
$$
PV=nRT
$$
である。$${T}$$を上げたいのであれば、体積を小さくし、圧力を上げればいい。そもそもこの条件では物質量も変化しそうであるから一概に言えない。
追記:空力加熱について
検証会メンバーNから空力加熱の説明のほうが具体的でないかという意見を頂いた。ということで上記よりさらに補足する。大学専門レベルなのでマニアックな方だけどうぞ。
空力加熱は状態方程式の説明と似通っているが、簡単に言うと物体が音速を超えた速度を持つと衝撃波(ソニックブーム)が起こり、特に先端付近では圧力が高まり高温になる。
下に貼った文献の(7),(8)から空気の比熱比1.4、気温を10度(283K)とすると
$$
\frac{p_2}{p_1}=1+\frac{2\gamma}{\gamma+1}(M^2-1)\\
\frac{T_2}{T_1}=\frac{\gamma-1}{\gamma+1}(1+\frac{2\gamma}{\gamma+1}(M^2-1))
$$
となる。先端温度は3500度(3773K)であるから、マッハ約8、圧力は78倍となる。ボールつぶれるわ。月光さんのマッハより絶対早いだろ。
・ナトリウムランプと同じ現象が起きた
上記2つが頼りないので、副査Mにオレンジ色の発光はなにかないか(テニスボールとはいっていない)と相談した際にもらった意見である。ありがとう。ごめん、2人にテニスボールって伝えればよかったな…。
確かにオレンジ色の発光はできる。しかし、晴れの日にアーク放電は流石に難しく、ナトリウムは汗とかでなんとかなっても(ならない)ネオンやアルゴンが必要である。両方一応空気には微量だが含まれているが、流石に濃度が足りない。
やはりどの方法でも難しい。どうやって光らせたんだ。かめはめ波見たいな感じで気とかそっちの話だろうか…。
追記1:化学的な構造変化について
主査Kから衝撃による構造変化により発光したのかもしれないと提案を受けた。あったらかなり良さそうな意見だが、主査も確認してくれたが探したところ、そのようなものはなさそうだった。残念無念…。
追記2:感圧塗料について
検証会メンバーNから感圧塗料じゃないかとのことを教えてもらった。感圧塗料とは簡単に言うとその名の通りで圧力によって色が変化する塗料である。
しかし、壁を破壊されるくらいの衝撃がある球にかかる圧力は相当のものであるため、現実的でないかもしれない。
肩にジャージをかけながらテニスをすることはできるのか?
常勝立海の部長、幸村精市さんは神の子と呼ばれるくらい強い。しかし、ただ勝つだけではない。なんと、幸村さんは肩にかけたジャージを落とさずに勝利するのだ。

もちろんテニスは肩にかけたジャージを落とすゲームではない。普通にプレイして勝つのである。すごい。何て美しくかっこいいんだ。
現実では勝つ以前にテニスの際にジャージをかけながらではまともに試合できなそうだ。どういう仕組みなのだろうか。幸村さんの魅力の1つである肩掛けジャージについて検証した。
今回も以下仮説を立てた。
①肩あたりに磁石でくっつけている
②とても摩擦係数が高いジャージを羽織っている
③落とさないように工夫しながら動いている
なお、マジックテープも考えたが、それでは落ちないと考えたので割愛した。
どれも可能そうであるが、幸村さんのカッコよさ、美しさを考えると③である。
現実で実際に実験してみた。残念ながら手元に立海ジャージはなかった。しかし、流石に軽いジャージだと落ちそうだったため、静止摩擦力が高くなるよう、重めのスカジャンで動きを観察した。
幸村ゲームというものがあるらしい。それを行ったことがある人はわかるかもしれないが、意外と上下左右にジャンプしたくらいでは落ちない。しかし、腕の角度が約90度以上になると落ちてしまった。
また、画像の通り幸村さんは原作(Genius371)では資料のように腕の角度には気を使っているように見える。

万が一落ちそうになっても自分で戻すことはできそうなので、ジャージが落ちないように角度を調整し、時には引っ張って戻したりしている可能性が高い。肩にかかったジャージにも気を使いながらテニスをできるという余裕。それが幸村さんの強さを示しているということだ。
「…というわけで幸村さんはすごくてかっこいい」
「でもさ、これ科学関係ないじゃん」「……」
不二の三種の返し玉(トリプルカウンター)の白鯨
不二の三種の返し球(トリプルカウンター)の1つ白鯨について検証する。

白鯨はアウトかと思われるくらいコート外に出た打球を風の力によって入れる技である。
不二の返し球はテニス経験者曰く、どれも現実では(人間工学的に)不可能とされているが、科学的にはどうだろうか?
白鯨についての検証は結構難しく、専門的な知識使う。そのため流体力学を専攻していた検証会メンバーNに任せた。ありがとう。ごめんなさい。でもちゃんと理解して書いたよ。
この先大学レベルになるので結論だけ先に書く。物理的に可能ではあるが、風が嵐並みに強い状態でテニスをやりながら、プロ選手の2倍の回転数をボールにかけないといけない。
因みに風速は14 m/sで、台風並みである。テニスは8 m/s以上で影響はあるらしいので、なかなかテニスできる状況ではないはずである。雨ではないにしろ、この風速は悪天候の中で竜崎先生がリョーマとの試合を止めたときより荒れていそうである。竜崎先生、止めてくれ。
後者については天才不二周助なのでラケットの両面使って回転数を稼げるだろう(?)。こちらは問題なさそうだ。つまり、天才不二周助なら風が強く吹いていれば白鯨を行うことは科学的に可能である。
・白鯨を導出するまでの計算
白鯨を考察するにあたって計算したものを示す。明らかに大学専門レベルなので、一部マニアックな人だけ見ていただければ幸いである。誰でもわかるようにする解説は長くなるので省略します…。また、白鯨では跳ねた球が不二の元に返ってくるが、それも考慮しない。
最初に前提条件として、コートの大きさを画像のようにする。不二はサービスライン付近にいるので、打ってからボールが地面につくまでの距離はおおよそ18m程度だと仮定する。なおここに示す式で||は絶対値、太字はベクトル(3次元座標空間)、×は外積である。
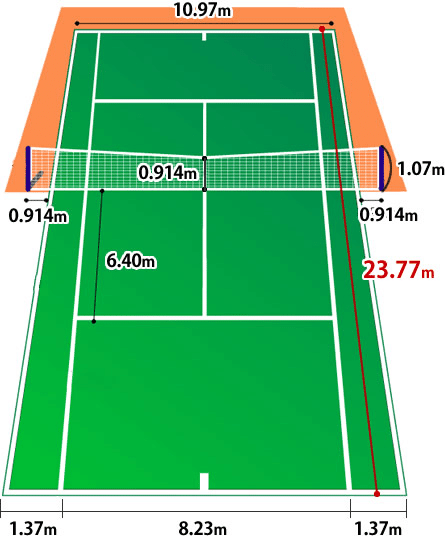
Uターンしてから着地した距離と不二の距離が18mであることを目指す。そのため、距離を出すには速度を積分する必要がある。まずは運動方程式から始めよう。球の飛距離球の質量、球の速度、時間、抗力、揚力、重力をそれぞれ、$${m、\bm{V_p}、t、\bm{Fd、Fl、Fg}}$$とすると、
$$
m\frac{d\bm{v_p}}{dt}=\bm{F_d +F_l +F_g}
$$
それぞれの力を見てみよう。風速と球の速度の相対速度、風速、抗力係数、空気の密度、球の投影面積、球の半径をそれぞれ$${ \bm{V=V_f -V_p、V_f}、C_d、ρ、A=πr^2、r}$$とすると$${\bm{F_d}}$$は
$$
\bm{F_d} =\frac{1}{2} C_d ρ A\bm{|V|V}
$$
揚力係数、球の回転の角速度を$${C_l、\bm{ω}}$$とすると$${\bm{F_l}}$$は
$$
\bm{F_l} =\frac{1}{2} C_d ρ A|\bm{V}|^2 \bm{\frac{V×ω}{|V×ω|}}
$$
$${F_g}$$は重力なので、
$$
\bm{F_g}=mg(0,0,-1)
$$
なお、$${C_d}$$は球の抗力係数であり、下記に示す($${Re}$$はレイノルズ数)。

これらの式より、非線形微分方程式だから解析的に解く事ができない。そのためシミュレーションでなければ説くことが難しい。簡単なシミュレーションで検証する。
検証に使用したサイトは下記リンクである。

原作を参照すると、不二の打ったボールの角度は30度ほどに見える。また、その他数値はテニスボールのものを使用した(野球ボールと書いてあるが値を変更してある)。初速を一定にして、回転数を変化させてシミュレーションした。
一般的なテニスプレーヤーの回転数は~80rpsであることを念頭に置いて調整したところ、上記結果になった。しかし、この風速は屋根が吹き飛んだり、煙突が折れる可能性があるくらいの風速である。

上記は不二が天才であることを考慮し、現実的(?)な風速までという制約の中シミュレーションした結果である。この結果より、一般的なテニスプレーヤーの2倍以上回転を与えて、嵐並みの風速であれば白鯨は可能だということはわかった。
テニスでブラックホールは作れるか!?
最後に今回のきっかけを作ってくれた、徳川のブラックホールだ。徳川はラケットを振ることによってブラックホールを出す。それによりボールを引き寄せることができるのだ。すごすぎる。

一応特徴を下記にまとめた
・徳川がラケットを振ってブラックホールを出す
・副作用として、30分やると血を吐く(その前にダメージを受けているともっと短い)
・ブラックホールは留まることができる(アニメ新テニスの王子様 U-17WORLD CUP 第3話)
・ブラックホールの隙を突くことができる(〃)
なるほどさすがにブラックホール程のものを出すには中々大変そうである。徳川の身体がとても心配である。
物理学徒をテニプリから遠ざけさせたブラックホールだが、その気持ちもわからなくはない。なぜならブラックホールはとんでもないものだからである。
ブラックホールは簡単に言うとその物体自体の質量が重すぎることで重力が強く、光さえも抜け出せなくなったもののことである。そのため、本来ボールを引き寄せるというレベルのものではない。そして簡単に出せるものではない。従って下記2通り考えられると思う。
A.本当に定義通りのブラックホールである
B.そもそもブラックホールという技名だけ
・A.本当に定義通りのブラックホールである場合
まずはブラックホールであるという前提で考察しよう。
本物のブラックホールであるとするならば、考慮しなければいけない範囲がある。それはシュバルツシルト半径というものだ。それは光さえも戻ることができない半径で、シュバルツシルト半径$${r}$$は物質の質量を$${M}$$,万有引力定数を$${G}$$($${G≒6.7×10^{-11}\mathrm{m^3/kg ・s^{-2}})}$$とすると下記式から導出できる。
$$
r=\frac{2GM}{c^2}
$$
因みに上記式より地球と太陽のシュバルツシルト半径は半径約1cm、太陽は約3kmであるため、その天体程度質量を持っていたとしても、そこまでつぶさないとブラックホールにはなれない。
もしシュバルツシルト半径内に入ってしまうとボールを打つ前に潰れてしまう。それをスパゲッティ化現象という。具体的には下記図に示すが、ある方向では潰れ、ある方向では伸びてしまい、まさにスパゲッティのようになってしまう。

俺で遊んじゃいけねーなあ いけねーよ!(桃ちゃんごめんね)
桃ちゃんの顎がさらに伸びる
そもそも徳川の出したブラックホールはラケットを振った軌道のように見えるため、質量を持つのかという疑問はある。ラケットの軌道の中心を半径とすればいいのだろうか。仮に質量を地球程度持っていたとしても半径1cm程度となるため、そもそもスカスカである。フランケンシュタイナーでなくても隙間を突くことは楽勝である。
ではブラックホールはとても小さく、シュバルツシルト半径外でボールを引き寄せているのだろうか?実際に軽く計算してみた*が、結果としては50kgの人が受ける重力程度の引力を得るには、$${1.3×10^{14} }$$ kgの重さが必要あり、U字マグネット程度の引力(5.9 N)であれば$${1.5×10^{12}}$$ kgの重さが必要である。これは小惑星イトカワより重い。無理があると思われる。
つまり現実で徳川のブラックホールを起こせるかというと、不可能である。
・B.ブラックホールという技名だけである場合
やはり本物のブラックホールは無理そうなのでブラックホールという技名だったと考えて考察する。これなら物理学徒だった友人も安心してくれるだろう。
これも3通り仮説を立てた。
①手塚ゾーン的なテクニック
②身体に磁石、ボールには金属を入れている?→徳川はそんなことしない
③真空を起こし圧力差により引き寄せている
①手塚ゾーン的なテクニック
一番有り得そうなのは手塚ゾーン的な原理で引き寄せている説である。
身体にも別の方向で負荷がかかってるので似たような現象なのだろうか。ただ手塚ゾーンが物理的、もしくは人間工学的にてきるかはまた別の検証が必要である。
②身体とボールに磁石を仕込んでいた
最初に言っておく。一番あり得ない。
身体に強力な磁石をいれると内蔵に穴が空いたりして本当に危険だが身体には負荷がかかるのでその点はあり得る。ダメ、ゼッタイ。
ただ徳川は義で世界を獲ることを証明しようとしているのでこの仮説は絶対ありえない。そのためこの仮説はここまでにしておく。
③真空を起こし圧力差により引く寄せている
最後に考えられるのが、低圧を作り、圧力差を作り引き寄せている可能性である。天気予報でお馴染みだが、風は基本的に高圧部から低圧部にかけて流れる。つまり、周りより低圧にすればその部分にボールが引き寄せられるかもしれないと考えられる。そういえば鬼さんが空間を削り取るとかなんとか言っていたが、これのことだろうか?
限られた空気の中であれば、低圧にするには状態方程式より密度(物質量)を減らせばいい。それにはラケットを振り、ブラックホールの箇所の空気を追い出すのだろうか。しかし、ラケットはガットがあるため空気を通し、周りの空気は無限大にあるので難しい。光る打球の燃える現象と同様である。
追記:ペポ
副査Rからカービィのように周りの空気を巻き込んで吸い込んでいるのではないかという案が出た。ただ口を開けている描写はないので、ラケットで吸い込ませているのだろうが、やはりラケットはスカスカなので難しいだろう。スマブラでカービィに吸い込まれ変身した徳川カービィを見てみたくなった。似合いそう。
やはり現実ではテクニック以外でボールを物理的に引き寄せることは難しいようだ。そうだったとしてもブラックホールは留まらせることは難しいと思われる。現実で意図的にブラックホールを作るには大型粒子加速器のあるCERNで実験するしかなさそうだ。
*引力の計算過程を載せる。
ブラックホール内の謎物質の仮質量を$${M}$$,テニスボールの質量を$${m}$$とすると、ブラックホール内にある謎の物体とテニスボール間の引力$${F}$$は、
$$
F=G \frac{Mm}{R^2}
$$
と表される。仮にテニスボールとブラックホールの軌道の中心部の距離を$${R=1}$$m,テニスボールを$${0.058}$$kgとする。50kgの人が地球から受ける引力と同等の力の場合の質量を$${M_1}$$,U字マグネットが引き寄せる引力程度の力の場合の質量を$${M_2}$$とすると、それぞれ$${M_1=1.3×10^{14}}$$kg,$${M_2=1.5×10^{12}}$$kgである。小惑星イトカワの質量は$${3.5×10^{10}}$$kgなので、それよりも重い。天文学的質量である。
しかし、本来、ブラックホールの中心部はライン上になっているため、ある一点の質量のみを考えている上記例は見当外れだと思う。ブラックホール内の仮の質量が、大体これくらい必要だとわかっていただければそれで充分である。
科学って楽しいじゃん!
残念ながらすべて現実の科学で証明可能というわけにはいかなかった。そのため違和感を覚え、テニプリから去ってしまう人もいるかもしれない。しかし、この表現がテニプリを楽しくしているのだと思う。また、何度も言うが科学的に証明できなかったとしても本当に面白いので、ぜひ戻ってきてほしい。
今後もテニプリ、テニプリを題材としたさまざまな考察、そして皆様の推し達の発展を願う。
最後に、こんなよくわからない遊びに付き合ってくれた5人の友人N,P,K,M,Rには感謝しかない。本当にありがとう。今度焼肉とか行こう。
なお、今回は物理を真剣に学んでいた友人たちに確認をとってもらったので、恐らくひどい間違いは無いと思われる。もし、なにか間違いがありましたらご連絡ください。質問も受け付けます。わかる範囲で…。
絶対ないと思いますが、上記は一個人が記述したなんちゃって科学ですので、全く保証できませんし自信ありません。参考にしないでくださいね。

乾かっこいい。
このnoteの知識は捨ててください。
上記まででブログのメインとなるところは終了した。しかし、有名な物理の問題を追記する。興味がある方は下記もお付き合いいただけると大変うれしい。
シュレディンガーの猫
シュレディンガーの猫を知っているだろうか。量子力学で使われる思考実験だが、ぜひ知らない方は覚えて帰っていただきたい。とても利便性が高い言葉である。
概要をざっくり説明する。外から観測することができない鋼鉄の箱の中に猫さんと放射性元素がある(いる)。放射性元素は1時間に50%の確率で放射性崩壊する。崩壊すると、計測器が反応し、寿司が支給される仕組みであるとする。猫さんが寿司を食べる確率が100%だとする。一時間後に、外にいる観測者にとっては図のような猫さんは寿司を食べていると同時に食べていないという重ね合わせの状態になる。なぜか。箱の中は見えないため観測できないからである。
量子力学はとても不思議なものである。単一光子の2重スリット実験でもあるように、波動性質を持つ為、スリットのどちらとも光子が出ているのかと測定器で確認すると、粒子の性質になるのだ(ファイルP4)。
つまり、観測しないと二つの現象が重ね合わせて存在するということである。にゃんとも不思議だにゃー🐈
因みによく高校などで原子核の周りに電子が衛星のようにクルクル回っているような説明を受けるがあれは厳密にいうと嘘である。本当は電子は雲のように確率的に分布していて、観測するまでどこにいるかわからない。軌道の形状はいろいろな種類があるから気になる人は混成軌道で検索してね(中高校生の方は受験があるかもしれないので↑は無視して学校の指示に従いましょう)。

シュレディンガーのキクマル(猫)
箱の中身が見えない状態だと↑の状態は同時に存在することとなる。
シュレディンガーの猫は本来残酷なルートに行く可能性もあるため、
ここでは寿司を食べるか食べないかに置き換えている。
この記事が気に入ったらサポートをしてみませんか?
