
2023年本試験問題 第2問 文字をどう伝えるか

辰己丈夫(放送大学)
今回取り上げるのは,2023年1月に実施された大学入学共通テストの「情報関係基礎」第2問です.この第2問の位置づけなどは,大学入試センターの資料などを見ると分かりますが,手短に書くと「アルゴリズム」や「数量的関係」を重視した問題となっています.2022年からの学習指導要領における「情報I」でも,モデル化とシミュレーションは当然,取り上げられる話題ですから,この問題に取り組んでみることも悪くないでしょう.
本稿では,まず,問題を解く受験生の気持ちになって考えていることを記していきます.その後,この問題の背景などについて説明します.
解答の作成
まずは背景の説明から
では,早速問題に取り掛かりましょう.

ソリティア? シャッフル? カードゲームの何かかな?と思いながら問題文を読み進めてみると,(あとになると)どうも,カードゲームとは無関係なことが分かります.「ソリティア」も「シャッフル」も,単なる名称のようですね.どんな格好をしているのでしょうか? トランプのキングのイラストのような感じかな?などと,ついついいろいろ考えてしまいますが,そんなことを考えていては問題に取り掛かれません.
大事なことは,「通信文を暗号化する」ということだけです.そこを理解して,イメージが広がるのを阻止して,粛々と読んでみましょう.

平文(「ひらぶん」と読みます)は4種類の文字を使うけど,暗号文は2種類しか使わない,という設定です.
最初は簡単な暗号化・符号化のルール

ということで,表1を参照します.

この表1を使って,1文字ずつ変換します.

【ア】は,単純に1文字ずつ当てはめるだけですから,簡単ですね.

これより,「①♡♠♠♡♠♠♠♠♠♡」が正解です.

【イ】は,ちょっと工夫が必要です.表1の下を見て,上側を当てる必要があり
ます.
まず,暗号文♠♡♡♠♡のもとになった平文は,何文字なのかが,表1だけではわかりません.仮に4文字だったと仮定して表を作ろうとしても……

ということで,区切りが分からない状況になります.でも,暗号文を左からじっと見ると,あることに気が付きます.ここでは,注目するところを黄色にしてみました.

ということで,平文「①♠♡♠」を暗号化したもの,と決定できそうです.
念のため,検算もしておきましょう.

無事にできてますね.

【ウ】も同様に見ていきましょう.

ということで,平文「⑧♢♣♠♠♡」を暗号化したものと決定できました.
問1の最後に,このルールについて分かることを探す問題があります.

ということで,解答群を見ます.

表1を見ながら,1文字ずつ平文に戻そうとしてみると,「⑤♠♠♠♠」だけ,平文に戻せないことが分かります.これが正解です.

ということで選択肢を見てみましょう.

ちょっとびっくりしますが,落ち着いて考えます.「得られることもない.」ということですから,反例,すなわち得られるかどうかをチェックすればいいのです.
たとえば,「⓪文字数が奇数の文」と「①文字数が偶数の文」はどちらもありますね.♡の1文字だけを暗号化すれば文字数は奇数ですし,♠の1文字だけを暗号化すれば文字数は偶数です.
同様に,「②♡より♠を多く含む文」と「③♠より♡を多く含む文」も,すぐに例を作れます.
そして,「⑤♠♠で終わる文」も♢の1文字だけを暗号化すれば例になります.
消去法で「④♡♠で終わる文」が正解のように思えますので,念のためチェックしてみましょう.表1で,暗号文が♠で終わっているのは,平文が♢のときだけです.そして,そのときは♠♠♠が終わりです.したがって,「④♡♠で終わる文」は存在しないといえます.
文字が書き換えられちゃった

この問題では妖精が登場します.どんな姿なのだろうか,というか,この非現実的な設定でいいのだろうか……と,ついついいろいろ考えてしまいますが,そんなことを考えていては問題に取り掛かれません.イメージが広がるのを阻止して,粛々と読んでみましょう.

ここだけ読んでいて,何をどうなっているのか,よく分からないですね.さらに読み進めます.

ここで実例が出てきました.加える方法は分かりましたが,でも,妖精はどこに行ったのでしょう?ということを考えつつ,先に進めます.

解答群を見ましょう.

ここは,とりあえず♡が3つあったので,おまけは①♠と分かります.妖精,そろそろ来るのかな?と思いつつ,読み進めましょう.

なるほど……ここで妖精のいたずらと「おまけ」の関係が明らかになりました.♡の個数が奇数個で送り出されているのに受信文には♡は4個しかない.ということから,【キ】は⓪♡ですね.
ところで,「いたずらで書き換えられた文字を復元しやすくなる.」って書いてありますね.この例だけを見ていると,「いたずらで書き換えられた文字を復元できる.」と言えそうなのに,「しやすくなる.」ということは,どういうこと?と思いながらも,さらに読み進めます.

ということで解答群を見ましょう.

ここで,おまけの付け方のルールを再掲します.
暗号文中の♡の数が偶数なら,おまけとして♡を文末に加える.
暗号文中の♡の数が奇数なら,おまけとして♠を文末に加える.
選択肢をじっくり点検しましょう.おまけの付け方は,♡の個数が偶数か奇数かによって違っているので,選択肢のうち,♡の個数に関係していないものは不正解です.残りを見比べると,「②♡の数が奇数の文」が正解と分かりますね.

落ち着いて考えましょう.通信文(暗号文)の♡の個数は必ず奇数です.
♡が♬に変わったものが届いたら,受信した文の♡の個数は偶数になります.
♠が♬に変わったものが届いたら,受信した文の♡の個数は奇数になります.
このように,因果を推論していくと,【ケ】は,「④♡の数が偶数の文」が正解と分かります.

ここで,さきほどの「しやすくなる.」という伏線が回収されました.つまり,妖精が1文字だけ変えたのなら,確実に復元できるけど,2文字を変えた場合は復元できない,ということになります.
さて,受信文「♠♡♠♠ ♬♬ ♡♠」には,♡は2個含まれていますね.送信時には♡は奇数個あったはずで,2文字が妖精によって変えられたのですから,送信時には♡は3個あったと考えるのが妥当です(1個でも,5個でも,7個でもない).ということは,♬♬の部分は,「①♡♠」か「②♠♡」のどちらかであったと推測できます.でも,このどっちだったのかは,これだけでは分かりません.
さて,残りの文章を読み進めていくと……

ということで,衝撃を受けました.妖精が2文字を変えることについて検討したのに,そんなことはない……とは.打ちひしがれた気持ちのまま,次の問いに移りましょう(そういえば,本問冒頭によれば,この妖精は「音楽」も好きなのですが,この伏線は「♬に書き換える」以外には登場してないのも気になってしまいます).
暗号を解読するよ

なんだか不穏な話になってきました.皇帝とか手柄とか,ちょっとこわい話が続きますね.平和な社会がいいな……などと,ついついいろいろ考えてしまいますが,そんなことを考えていては問題に取り掛かれません.本問は暗号を解読されたくない,ということがテーマのようです.イメージが広がるのを阻止して,粛々と読んでみましょう.

私たちは,表1を見ていますから,この「情報1」が正しいことは知っています.そして,盗聴者がこのことを推測したということを,私たちも知ったということです.

ちょっと分かりにくいことが書かれてきました.あらためて,表1を見ましょう.

あれあれ? 表1と情報2って,矛盾してませんか?と思ってしまいますよね.でも,盗聴者は表1を知らないのです.だとしたら,この情報2って,どういう意味なんだろう?って考えてしまいますね.とりあえず,問題文の先を読むことにしましょう.

あれあれ? また,ちょっと理解しにくい状態になりました.「さらに,スパイに収集させた大量の平文と暗号文から」ということは,「平文と暗号文の関係は,スパイが分かっている」のではないの? そうだとすれば,暗号文をつくる表1は,丸見えになってませんか?と思ってしまいます.しかし,ここでは「大量の平文と暗号文から」と書かれていますが,「大量の平文と暗号文の関係から」とは書かれていないのです.つまり,次のものがある,ということにすぎません.
暗号文がどうなっているか分からないけど大量の平文
平文がどうだったのか分からないけど大量の暗号文
しかし,まだ分からないことがあります.それは,♬の状況です.暗号文から何か分かったとして,♬のことはどこに書かれているのでしょうか.いまのところ,問3では♬について何も言及されてません.ちょっと気になりますが,きっとこの先に書いてあるのでしょう.
という状況を理解できたところで,表2と表3がこちらです.なお,あとの解説のために,表3はオリジナルの下に1 行加えてあります.

さて,王子と一緒に暗号を解読しましょう.

解答群を見ましょう.

ここでやっと,情報2の意義を理解できました.つまり,「♡ → ♠」と仮定すれば,♠を切り出す「♠ → ♠ 何か」や,「♣ → ♠ 何か」や,「♢ → ♠ 何か」になることはないのです.つまり,♠,♣,♢のどの3文字も,暗号化した結果は「③♠ からは始まらない」と言えます.

ここは簡単ですね.表3で,♠で始まる4つを加えましょう.$${{r}}$$$${_{5 }}$$+ $${{r}}$$$${_{6}}$$ +$${{r}}$$$${_{7}}$$ +$${{r}}$$$${_{8}}$$ = 10 + 20 + 20 + 10 = ⑥60%となります.ちなみに,平文の方で文頭が♡となるのは,表2によれば40%です.自然言語なので多少のズレもあるでしょうけど,40%と60%の違いは,集めてきたサンプルが多量であるならば,「平文♡40% → 暗号文♠60%」と結び合う関係と言えないと考えるのが妥当です.

これも表3を見るだけです.$${{r}}$$$${_{7}}$$ + $${{r}}$$$${_{8}}$$ = 20 + 10 = ③30%が正解です.

途中のプロセスは省かれていますが,ここで♡ → ♡が分かったということは重要ですね.ちなみに,$${{r}}$$$${_{1}}$$ + $${{r}}$$$${_{2}}$$ + $${{r}}$$$${_{3}}$$ + $${{r}}$$$${_{4}}$$ = 40% となります.

ここは,いままで考えたことを理解できていれば,情報2に矛盾しない状況を選択します.上記の推測が正しければ,♡以外の文字を暗号化したとき,♡で始まることはないわけです.つまり「②♠から始まる」といえます.

ということで,表2を見ましょう.
文頭が♠の平文の割合は,30%
$${{z}}$$が文頭の暗号文の割合は,10%,20%,20%,10% の中から2つを選んだ和
となります.このことから,次の結論がでます.

$${{z}}$$は♠♡となるのは,$${{r}}$$$${_{5}}$$ + $${{r}}$$$${_{6}}$$ = 30% で妥当.
残りが,$${{r}}$$$${_{7}}$$ + $${{r}}$$$${_{8}}$$ = 30% で,これは暗号化された文字列が【タ】③♠♠で始まる.
ここまで頑張って推論してきました.いよいよ最後……かな?

方法Aは,まさに正解そのもの.暗号盗聴成功となります.もう1つの方法Bは,すでに【タ】が♠♠に決まっているので,表3を見て♠♠で始まらない2つを選びます.
表2 によれば,♣は20%,♢は10%
表3 によれば,♠♡♡は10%,♠♡♠は20%
ということで,次のとおりに決まります.
♣ → ⑨♠♡♠
♢ → ⑧♠♡♡
これで,本問終了したのですが,最後になにか書かれています.

ここを見て,さて,今までの問題で,何か誤解したところ,あったかもしれないですね.あらためて,答案を見返してみましょう.王子がおまけのことを知らなかったなんて,いま,初めて説明されました.でも,問3を解いている間に,♬は出てこなかったです.ということは,問3は,当初から♬のことは考えなくてもいい問題だということが,最後になって分かりました…….
おつかれさまでした.
★解説
さて,この問題,いろいろなことを検討しながら解いてきました.かなり大変な問題でしたが,実は,情報科学の常套手段とも言うべき定番の考え方を知っていると,いくつかの設問には,見通し良く解くことができます.
ここでは,その理論について述べておきます.この解説では,分かりやすいように,平文の文字を♡♣♠♢とし,暗号化されたものをH,Sで表します.

木構造
木構造というのは,まさに植物の木のようなデータ構造のことです.スタート地点から,分岐して,進み,また分岐して……となって,あるところで端点に着いて終了します.ここでは,表1を木構造で表現してみます.

この木は,符号化の方法を示したものなので,符号木と呼ばれます.
この符号木を見ながら,あらためて【ア】・【イ】を見ると,とても分かりやすいですね.

【ウ】以降も見通しが良くなります.
瞬時符号(瞬時復号可能符号)
ところで,このような「ルール」には,大事な条件があります.まず,「符号化された暗号は,戻せること」が大事です.たとえば,表1が書き換えられていて,次のようになっていたら,暗号を戻すことはできません.

これでは,暗号文を戻せなくて困ります.では次の例を見てください.

こちらの例は,暗号文を見ると元の文が決まります.「一意符号化」と呼ばれる性質です.しかし,決め方がやっかいです.たとえば,暗号文がHHSS だったとしましょう.

この場合は,暗号を解読していく作業をするときに,途中で「あれ? どっちかな?」と悩みながら進めなければいけない状況になります.ところで,このルールの符号木を見てみましょう.
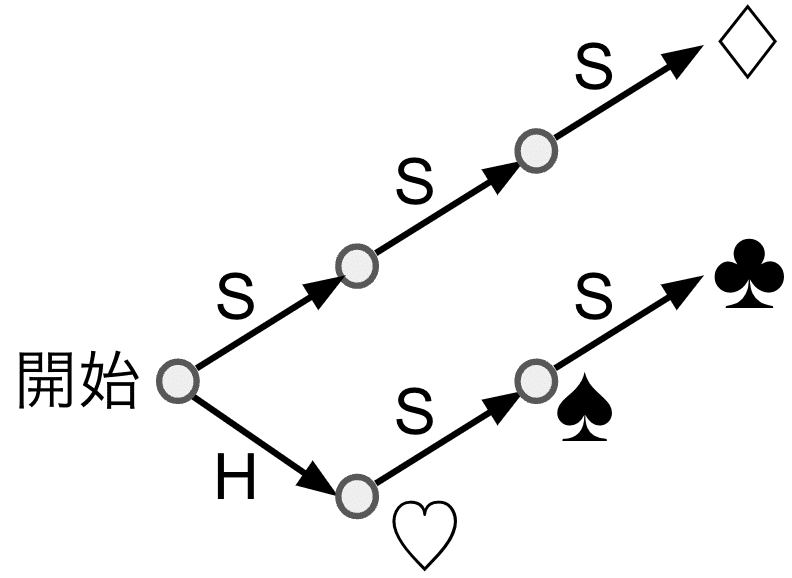
本問の表1から作った符号木とちがって,途中に♡,♠があります.つまり,「ここでやめていいのか,進んでいいのかは,先を見ないと分からない」のです.この方式は能率的ではないですね.
本問の方法は,上記に述べたような「うろうろ」はなくて,途中で決定できない状態にはならず,いつでも「確定しているか,次の可能性がまったくない」という状況になります.このような符号化の方式を瞬時符号(あるいは,瞬時復号化可能符号,接頭符号)といいます.
この瞬時符号の特徴は何でしょう? 実は,情報2が,まさにその性質なのです.

この性質は,図-2の符号木では成立してないことが分かりますね.実は,情報2は,この暗号化が瞬時符号である,ということを述べたものだったのです.
瞬時符号のことを知っている人が問3の情報2を見たら,「ああ,あれのことですね」と思い出すでしょうし,問題を解く際に見通しが良くなったでしょう.
パリティ検査
問2では,♡の個数が必ず奇数個になるように「おまけ」が加えられます.この「おまけ」を利用した方法は,パリティ検査と呼ばれる方法です.
通常,通信されたデータや,記録媒体(USBメモリ,Blu-ray/DVD/CDなど)に記録したデータは,送信(書き込み)したものが,そのまま受信(読み出し)されるように作られています.しかし,実際には異なる内容を受信する(読み出す)ことがあります.通信の途中では大きな電磁波の影響を受けたり,通信機器の電源電圧が低下したり(瞬間的に停電したり),さらには太陽の黒点運動の影響で地球の電離層に変化が出てしまったり,記録媒体に傷がついたり……など,さまざまな要因があります.
そこで,こういう誤りの有無を判断し,訂正(修正)する仕組みを考えておく必要があります.本問で紹介された方法は,通信内容の♡の個数を奇数にしておき,受信時に♡の個数が奇数のままなのかを確認する方法です.このときに加えられるおまけのことを「パリティビット」と呼びます.
通常は,通信の最中に発生する誤りは,次の2通りです.
「0」を送ったが,「1」で受信された
「1」を送ったが,「0」で受信された
したがって,パリティビットを利用した方法では,誤りが1つだけのときに発見できる,と言えます.なお,送信したビット数と受信したビット数が異なる場合は,この方法は使えません.
本問では,この内容が妖精によって,♬に書き換えられる,という事態が発生しています.これは,パリティビットの方法に似ていますが,若干違う誤り訂正の方法となっています.なお,通信文は♡と♠だけのはずなのに,♬を受信できるようになっています.おそらく,視認による通信方法のようですが,本問では,この部分はツッコミはされないことになっています.
パリティ検査のことを知っている人が問2の「おまけ♬」を見たら,「ああ,あれのことですね」と思い出すでしょうし,問題を解く際に見通しが良くなったでしょう.
なお,通常,パリティビットによる誤り検査方法を利用する場合は,発見できるのはたかだか1ビットです.この点は,本問でも取り上げられた話題です.また,通常の通信では,1ビットの誤りの場合は,(♬を使うことはないので)発見できても訂正はできません.発見と訂正を行うには,たとえば垂直水平パリティ方式と呼ばれる方法を利用します(詳しくは,調べてみてください).
頻度分析攻撃
正規の受信者以外のひとが暗号文を解読することを,暗号学では「攻撃」と言います.問3では,王子は平文の各文字の頻度(全体に占める割合)と,暗号文の各文字の頻度を利用して,暗号文の攻撃を試みています.
自然言語を使用した平文には,言語学的な特性があります.たとえば英語の場合は「一番多い文字はeである.一番多い2文字連続はthである.qの次にu以外の文字は現れない.」などとなります.ほかにもいろいろ知られています.また,使用されている時代や世代・地域によって,頻度の構成が若干変わってくることもあります.他の言語でも,それぞれ特徴があります.
今回,シャッフル王国が利用した暗号は換字式と呼ばれる,1文字1文字を変換する方法です.表1は換字表と呼ばれます.この場合,「元の自然言語の頻度」と「暗号文の頻度」が類似する,という性質があります.そこで,暗号文の頻度表を作って暗号を攻撃する方法のことを,頻度分析攻撃といいます.
頻度分析攻撃をするときは,平文と暗号文について,1文字の頻度表(「モノグラム」と言います),連続2文字の頻度表(「バイグラム」),連続3文字の頻度表(「トリグラム」)などを必要に応じて作成して,比較をしていきます.本問のような方法で暗号を攻撃されてしまうことが分かっているので,現代の暗号では,換字式を素直に利用することはありません.
頻度分析攻撃のことを知っている人が問3の「スパイに収集させた大量の平文と暗号文から,平文の文頭1文字と暗号文の文頭3文字の割合を集計し,次の表2と表3 を得た.」を見たら,「ああ,あれのことですね」と思い出すでしょうし,問題を解く際に見通しが良くなったでしょう.
ところで,頻度分析攻撃を行うときは,できろだけ実用的な頻度表を作ろために,平文の言語での文章と,暗号文を,それぞれ,大量に用意しておく必要があります.問3では,どれだけの文を用意できていたかは書かれていません.もし,表3の♡♡♡が10%という値が,非常に少数の文から得られた値であろならば,本当は10% よりも低いかもしれないし,高いかもしれない……となります.精密に推測すろ必要があろならば,統計学の知識・技法も必要となりますが,一方で,換字表の完成度が低くても,人間が書いた文章,すこしくらい間違えていても読めてしまいます.この段落のこの行以前の行では「る」とすべきところを「ろ」にしてみましたが,それで理解できない,ということはなかったですね.あまり統計的な追求を行わなくても,換字表を推定できろ..... できることが多いです.
そして,方法Aと方法Bの2つの方法が候補になりましたが,2つしかないのであれば,暗号文を両方の方法で復号し,自然言語として意味が通じる方を残せばよい,ということになります.
背景知識は必要?
さて,本稿の後半では,この問題の背景となる情報学の知識・技法について説明してきました.この内容,受験する際に必要かどうかを考えましょう.
後半で触れた内容のうち,符号木・瞬時符号と,頻度分析攻撃については高等学校情報Iの範囲ではありません.一方で,これらの内容を知っていると,本問以外の情報学の課題に取り組む際に役立ちます.本問に取り組む際にも見通しが良くなります.といっても,同様の知識や技法は,とてもたくさんあります.「すべての受験生が知るべき」ということではありません(時間は有限で,他教科も勉強しないといけないですからね!).将来,情報学にかかわる仕事を目指している人・現在働いている人なら,(たとえ高校生でも)知っておいてほしいのですが,そうでない方にとっては,結論なし……となりました.
なお,情報科を担当する高校の先生には,ぜひ知っておいてほしい項目です.ですが,先生は「知っていることを,全部生徒に覚えさせる」のではなく,生徒が考えるために必要な手助けとして,こういった知識を小出しにして,自律的に学べる生徒を育ててほしいと,私個人は思っております.
なお,暗号に関する高校生向けの入門書としては,参考文献2)と3)を挙げておきます.3)は本文の多くが換字式暗号で書かれた(?)本です.筆者は高校生のとき,3)のオリジナル本を頻度表を作りながら夢中になって解読しました.
参考文献
1)情報処理学会情報入試委員会:情報関係基礎アーカイブ,
https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK
2)一松 信:暗号の数理 ─作り方と解読の原理(改訂新版),講談社(2005), ISBN : 978-4062574907
3)泡坂妻夫,中井英夫,日影丈吉,長田順行:秘文字,復刊ドットコム(2020),ISBN : 978-4835457444
(2023年3月22日受付)
(2023年7月5日note公開)
■辰己丈夫(正会員)
1991年早稲田大学理工学部数学科卒業.2014年筑波大学博士(システムズ・マネジメント).1993年早稲田大学情報科学研究教育センター助手.その後,神戸大学.東京農工大学を経て,現在,放送大学教授.2020年より2年間,本会理事(新世代).本会広報広聴戦略委員会副委員長.ほかに,教科書委員会,会誌編集委員会,初等中等教育委員会,一般情報教育委員会など各委員.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
