
ロープ飛び移りゲームと動的計画法

久野 靖(電気通信大学)
おなじみ「教科『情報』の入試問題って?」,今回は,大学入学共通テストの2023年本試験「情報関係基礎」第3問を取り上げます(この問題を含むさまざまな問題のアーカイブは文献1)にあります).
なぜこの問題?ということですが,「情報 I」の試験が始まっていない現時点では,「情報関係基礎」の問題が参考にできる問題の最有力候補です.そして,毎回,第3問は「プログラミング」を題材としているので,取り上げてみよう,ということです.
そして,特にこの問題は,難しい解法をどれくらい知っているべきか,という悩ましい議論とかかわりがありますので,それについても後半で取り上げます.では,始めましょう.
ロープ飛び移りゲームって?
この問題では,「ロープ飛び移りゲーム」というものを規定し,その得点を高くするためのアルゴリズムとプログラムを考えていきます.最後には表題にある「動的計画法」(後で詳しく説明します)を使って,最適解を求めるところまでいくのですが,始めはもっと簡単なやり方から着手します.でもその前に,ゲームの説明から始めないと,ですね.

いかがでしょうか.要は,最初のロープで55mの高さにいて,次々にロープに飛び移り,どのロープでも下にだけ移動できて(下に移動しなくてもよい),最後のロープの0mの高さでゴールします.その間に,ロープに巻かれたリボンに触れると得点でき,その数をできるだけ多くしたいわけです.
ロープが11本,最初のリボンの高さが55m,最後のリボンの高さが0mに決められているのは考えやすくするということで分かりますが,途中のリボンの高さも表-1のように決まっていることになっています.アルゴリズム的にはもっとさまざまな配置に対応できるのですが,配置を限定した方が考えやすいという配慮からでしょうか.ちなみに,私の近辺ではこれについて「複数の配置を示すべきだ」「始めはもっと容易な配置がよい」「終わりの方ではもっと難しい配置を出してほしい」等,さまざまな意見が聞かれます.

配置が与えられたので,すこし具体的な動かし方を考えて見ます.ここで,水平移動とロープを降りるだけ,というのがポイントになります.たとえば最初のロープから55,53,31と連続してリボンに触れると,次の37,37の2本は31より高いので触れることができません.3本目の31をパスすれば,55,53,37,37と5本目までのロープで4点を獲得できます.このように各ロープで触れたりパスしたりというのを選択して高得点を目指す,というのがこの種の問題の要点です.
問1:意外な動かし方
なのですが,問1では「意外な」動かし方が出てきます.見てみましょう.

つまり,各ロープで5mずつ降りるというのです.リボンの状況にかかわらず決まった動き方をする,という点で「意外な」と私は感じましたが,皆様はどうでしょうか.もっとも,このような「決まった」動かし方が,最初は分かりやすくてよい,という考えもあるでしょう.
さてそうすると,各ロープで降りる前の高さは順に,55m,50m,45m,40m,35m,30mとなりますから,6本目の【アイ】は「30」,【ウエ】は降りた後ですから「25」となります.
得点は,各ロープで「降りる範囲」にリボンがあるものだけ1点を獲得しますから,表1と「降りる範囲」を照らし合わせた結果,ロープ1 (55m〜50m),ロープ4 (40m〜35m),ロープ11 (5m〜0m) の3本が該当し,【キ】は「3」となります.
さて次は,この動かし方による得点を計算するプログラムです.配列や変数の使い方がまず説明されていましたね(あと,ストーリー的には【キ】もプログラムを動かした結果となっていますが,実際には上でやったように,手で解く方が素直でしょう).

コードを見てみましょう.tokutenとtakasaは最初は0点と55mですね.次はiをロープ番号1~11まで変えながら繰り返します.その中は,【オ】なら得点を1増やす,そして高さを【カ】で置き換える,となっています.これらの穴の解答群は次にあります.
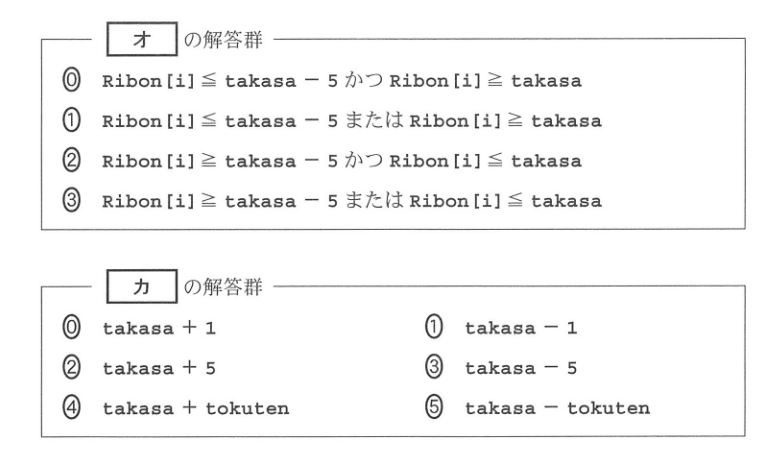
【オ】ですが,得点できるのは「リボンの高さが,降りる前の高さ以下で,かつ, 降りた後の高さ以上」です.まだtakasaを更新していないことに注意すれば, 「降りる前の高さ」がtakasaで,「降りた後の高さ」がtakasa - 5と分かります.そこで「Ribon[i] ≦ takasa かつ Ribon[i] ≧ takasa - 5」が正解としたいのですが,「かつ」の両側が入れ換えてあるので,「Ribon[i] ≧ takasa - 5 かつ Ribon[i] ≦ takasa」つまり②が正解です.
【カ】はもっと簡単で,高さを前の高さより5mずつ減らしていくので,「takasa - 5」つまり③が正解です.
問1の範囲で振り返ってみると,【ア~エ】はこの動かし方が読み取れれば正解できます.【キ】は表1のデータを通して得点を計算できれば正解できます.これらはアルゴリズムの問題です.【オ~カ】はアルゴリズムをどのようにプログラムに翻訳するかが分かっている必要がある,プログラムの問題です.
問2:普通の動かし方
さて,問2に進むと別の動かし方が出てきます.実際には,こちらの動かし方の方が「まず思いつく」普通のやり方だと思われます.

つまり,「リボンの高さが現在の高さ以下(等しい場合も含む)なら,リボンの高さまで降りて(0m降りる場合も含む),点数も1増やす」わけです.
今度は,この動かし方での得点を計算するプログラムをまず作ります.書いてありませんが,変数 tokuten,takasa,そしてロープ番号iの役割は先の問題と同じです.

穴は枝分かれの条件と高さの置き換え式の2つで,先の問題と同じです.ただし,さっきは「得点はある条件の時のみ,高さは毎回動かす」だったのが,こんどは「ある条件のときのみ,得点して,高さも動かす」になっています.この違い(コードで言うと「を実行する」と「takasa ← ...」の順番の違い),分かりますね? これらの穴の解答群は次のものです.

【ク】については,「リボンの高さが、現在の高さ以下(等しい場合も含む)」ですから,「Ribon[i] ≦ takasa」で②となります. 【ケ】については,「リボンの高さまで降りる」ですから,「Ribon[i]」で⓪となります.

次に,プログラムの途中 (i = 4) および最後における変数 tokuten,takasaの値をたずねる問いがあります.しかし,これらの変数は得点と現在の高さですから,アルゴリズムから考えてもできますね.

この動かし方では,4までの現在の高さは「55」「53」「31」そしてリボンの高さが現在の高さより高いので次は何も変化せず「31」です.したがって【サシ】は「31」となります.得点は最初から「1」「2」「3」そして次のリボンには触れないので「3」のままです.したがって【コ】は「3」となります.【ス】はこの動かし方で最後までいったときの得点で,触るリボンは「55」「53」「31」「22」「13」「0」の6つなので「6」となります.
これで問2が終わりそうなものですが,それでは十分でないと思ったのか,続く 8行でアルゴリズムの改良を取り上げています.
具体的には,条件「リボンの高さが現在の高さ以下(等しい場合も含む)なら,」を「リボンの高さが現在の高さ以下(等しい場合も含む),かつ,リボンに触れるために降りる高さがGENDO未満なら,」に直すという改良です(ただし,i=11 のときは最後なので,常に降りる).なお,GENDOは「試しに」20とするとなっています.
この変更は,【ク】の条件の穴を置き換えればできます.その新しい穴を【セ】とし,解答群を示しています.

【ク】との条件の結合は「かつ」なので⓪ ①のどちらかですが,i=11 のときはともかく(内側の条件の成否にかかわらず)降りるので,【セ】は「(... 内側の条件...)または i=11」すなわち①となります.
それはいいのですが,いままで【ク】の条件が生きていたのに,今度のアルゴリズムでは i=11 のときにこの条件を無視しています.気持ち悪いのですが,実はロープ11ではリボンの高さが0mであるため,条件【ク】は常に成り立つので,前のアルゴリズムでは「または i=11」がなくてもよかった,しかし今度はGENDOの条件があるのでそうはいかない,という仕掛けです.
問2の最後はGENDOを20としたときの得点を求めます.「55」「53」で,続く 31は降りる高さが GENDO 以上になるのでスキップし,「37」「37」「22」「13」で,あとは 13 より高い値が続いて,最後に「0」ですから,【ソ】は「7」となります.
問2について,振り返ってみましょう.【ク~ケ】はプログラムの穴埋めで,問1のプログラムとの違いをきちんと分かっている必要があります.【コ~シ】は変数の途中の値ですが,どちらかと言えばアルゴリズムの問題です.【ス】は問1で言えば【キ】のように,このアルゴリズムで最後まで動かしたときの得点が計算できるか見ます.
そしてこの先,アルゴリズムの改良版が登場し,【セ】でそれをコーディングする穴埋め,【ソ】で最後まで動かしたときの得点を尋ねています.1つの問の中にアルゴリズムが2つというのは,かなりハードな感じがしますし,【セ】の穴埋めの内容が複雑なので一層そう思われます.
問3:動的計画法
問3に進んで,いよいよ動的計画法が出てきます(この仰々しい名称は出していませんが).動的計画法をかいつまんで言うと,「大きさNの問題を解くのに,配列を用意して,大きさ1~N-1の問題に対する解を全部覚えおくことで,たやすく最良解を得る手法」です(正確には配列が2次元以上の場合も有り得ますが,そこは省略).では見てみましょう.

この「i=1 のとき,Kokomade[i] は簡単に求まる」「i ≧ 2 のとき,Kokomade[t](1 ≦ t < i) が求まっていれば,これこれの方法で Kokomade[i] が求まる」という,数学的帰納法によく似た説明が,動的計画法のパターンです.初めての方はかなり戸惑うと思いますが,落ち着いて理解してください.幸い,動的計画法はプログラムを作る段階では,比較的簡単なことが多いです.
では,文章とプログラムの両方に共通の,【タ】の穴を考えます.t 本目のロープのリボンに触れて,かつ,それより後の i 本目のロープのリボンに触れることのできる条件は「後者のリボンの高さが前者より高くない(同じか低い)」ですから,【タ】は「Ribon[t] ≧ Ribon[i]」つまり解答群の③になります.

コードを見てみると,まず Kokomade[1] ← 1とした後,i を2から11まで1ずつ増やしながら Kokomade[i] を求めていきます.この順なら,i 番目を求めるときには,1~i-1番目はもう求まった状態にあり,動的計画法の条件が保たれることになります.
そのループの内側の(03)-(08)のところで,t=1, 2, ...,i-i かつ【タ】の条件が成り立つ Kokomade[t] の最大値を求めて,変数 saikouに入れています.i 番目のロープではその値にこのロープのリボンに触った1点を加えますから,【チ】は「saikou+1」すなわち①になります.

このように理屈は分かりにくくてもコードは比較的単純なので,それで終わりにはしにくいからでしょうか,続いて,i=3, 4, 5 のときの Kokomade[i] と,最終的な最高得点つまり Kokomade[11] を尋ねています.


表1を見ながら判断してください.ロープ3はロープ2から来られますから,【ツ】はロープ2の Kokomade[i] に1を加えた「3」.ロープ4はロープ3からは来られず,ロープ2からなので,【テ】も「3」.ロープ5はロープ4から来られるので,【ト】は「4」.ロープ6はロープ5からで5,ロープ7はロープ6からで6.この先がリボンの高さが高くなるので注意が必要です.ロープ8はロープ6からで6,ロープ9はロープ5からで5,あとはロープ10はロープ8からで7(得点が高いものを選ぶこと!),そしてロープ11すなわち【ナ】はロープ10からで「8」となります.
問3について,振り返ってみましょう.この問はとにかく,解法が分かりにくいのですが,誘導にしたがって【タ~チ】の穴を埋めるのは解法を完全にマスターしなくてもできそうです.続く【ツ~ト】も,そこまでの最良値ですから,解法をマスターしていなくてもわりあいできます.【ナ】は解法が分かっている人向けですが,それらしい値を入れて正解する人もいるかもしれません.
そして,あまり手間でなく最適解が求められる,というのも動的計画法を採用した恩恵です.動的計画法を使わずに一般に最適解を求めようとすると,各ロープについて,そのロープで降りる場合と降りずにパスする場合の両方を考えることになり(ただしそれより前のロープの選択によってはパスしか選択できない場合もある),プログラムも大変ですし,その実行時間も多くなります.
動かし方を求める「トレースバック」
問3には,解法の理解を前提としなくても多くの問に正答できてしまうという難点(これは,解答者にとってはやさしくなっているという点で「慈悲」)があります. そして,もう1つの不満は,プログラムを作る目的が「どのようにキャラクタを動かしたらよいか検討」することのはずなのに,問3のプログラムでは動かし方が分からない,という点です.
実は,動的計画法では,解法を求めている最中は「1~Nに対する最適値を同時に求めている」ため,個別の動かし方は分かりません.動かし方を知るには,各 i に対する「どこからが一番優れていたか」(前節で「ロープXはロープYから来られる」と言っていたもの)の情報を覚えておき(これをトレースバック情報と言います),Nからこの情報を遡ることが必要です.
実際に問3のプログラムを直してみましょう.トレースバック情報も配列に入れる必要があるので,これを Koko_mae[i] という名前にします.(01)と(02)の間に次のものを入れます.

これは「ロープ1の前はない」に相当します.続いて,(06)と(07)の間に次のものを入れます.

つまり saikou を更新したときに,そのロープ番号を Koko_mae[i] に覚えます.そして,(11)の後にトレースバック情報をたどって表示する次のものを加えます.

表1の状況に対して,この拡張されたプログラムを実行すると,次の出力となります.トレース「バック」の名前どおり,最後から逆順に表示されていきます.

分量の問題からトレースバックまでは入れなかったと思われますが,結果の分かりやすさまで考えるなら,入れてほしかった気はします.
まとめ:動的計画法は学ぶべき?
そういうわけで,この問題は「ロープ飛び移りゲーム」について,問1で意外な動かし方,問2で普通の動かし方,問3で動的計画法による最適な動かし方を扱い,どの問でもアルゴリズム,プログラム,具体的な解を扱うようにできています.難易度は「題材にしては」やさしく設定されているように思います.
この問題について一番悩むのは,何といっても「動的計画法を学ぶか(生徒に学ばせるか)否か」でしょう.次の2説があります.
難しくて悩むだけなので,学ばない.この問題の問3のように,知らなくてもその場で理解できるように配慮されているし,完全に理解しなければいけない問題はあったとしても配点は少しだろう.
いろいろ役に立つ場面もあるので,頑張って学ぶ.そうすれば,この問題のようなものに出会ったときに安心していられる.マスターするのに少しかかっても,価値がある.
「いろいろ役に立つ」の例として,たとえばさまざまな「プロコン(プログラミング・コンテスト)」があります.プロコンでは,問題を解く時の計算量(計算時間)に制約を設けるのが普通なので,あるレベル以上の問題では動的計画法が必須となります.
とは言え,プロコン等はそれこそ「好きな人の」ものですから,普通に情報の授業を受けている人に常にお勧め,とは言えません.結局,ここの問3の解説を見て「わかった,もっと学んで見たい」と思った人はどうぞ,ということでしょうか (たとえば文献2) には動的計画法も含めてさまざまな手法が解説されています).
明確な結論がないのは申し訳ないですが,この問題をきっかけとして,動的計画法というものがある,ということを頭の隅にとどめていただければ幸いです.
参考文献
1)情報関係基礎アーカイブ,情報処理学会 情報入試委員会,
https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK
2)秋葉,岩田,北川:プログラミングコンテストチャレンジブック[第2版],
マイナビ (2012).
(2023年3月24日受付)
(2023年6月5日note公開)
■久野 靖(正会員)
電気通信大学 特命教授,筑波大学 名誉教授.理学博士.プログラミング言
語,ユーザインタフェース, 情報教育に興味を持つ.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
