
南山大学のサンプル問題

中西 渉(名古屋高等学校)
南山大学のサンプル問題
南山大学は2024年3月26日に「情報」が入試に導入されることについての説明会を開催しました.全学統一入試(個別学力試験型)の理工学部の理科・情報では「物理基礎,物理」「化学基礎,化学」「情報I」から大問ごとに選択できることが発表され,同時にイメージをつかむためのサンプル問題が公開されました ¹⁾(脱稿後の,2024年7月19日に,サンプル問題が追加で1セット公開されました ²⁾).
情報のサンプル問題は情報-1と情報-2に分かれていて,情報-1はダークパターンをテーマにした問題と,変数の値の入れ替えに関する問題,情報-2は論理回路に関する問題でした.この記事では情報-2の論理回路の問題を取り上げてみます.
論理回路
この問題を見て「こんな回路のことは習っていない」という人もいるのではないでしょうか.確かに論理回路は教科書によって掲載されているものとされていないものがあります.だから共通テストでは出題されないかというと,そんなことはないでしょう.たとえば大学入試センターが公開した大学入学共通テスト試作問題でも論理回路の問題が出題されています ³⁾.
だからといって論理回路の記号や,半加算回路のようなよく使われる回路を暗記するといったことが重要だとは思いません.よく使われる回路(この問題も「多数決回路」と言われる有名なものです)を覚えようとしても多すぎてきりがありません.今の入試では,覚えたことを単にアウトプットするのではなく,与えられた新しい問題にその場で取り組むのがトレンドです.そしてそれは行き当たりばったりということではありません.普段の勉強が「考える」ものになっていることが求められているのです.
大学個別の入試問題は受験生や学校,社会への「メッセージ」でもあります.この問題にも「考えなさい.考える勉強をしなさい」というメッセージが込められているのだと,筆者は考えています.
サンプル問題
では具体的に問題を見ていきましょう.最初は論理回路の説明がありますが,この記事では省略します.
問1

2人以上が着席していたらランプを点灯させたいということですが,「2人以上」というのは2人または3人ということなのでそのまま考えると
AとBが着席,Cが非着席
BとCが着席,Aが非着席
CとAが着席,Bが非着席
AとBとCが着席
のどれかであればいいということになります.この4つのケースを考えてもいいのですが,非着席を調べる必要が本当にあるでしょうか.AとBが着席していればCの状態によらずランプを点灯させるのだから,Cの状態を調べるのは無駄なことです.数学だとこのようなMECE(漏れなく重複なく)な分け方を考えがちですが,論理回路やプログラミングではそれがかえって無駄になることがあります.
だからこの場合は次の3つのどれかであればいいのです.
AとBが着席
BとCが着席
CとAが着席
これを論理式で表すと次のようになります.A,B,Cが着席していることをそれぞれ$${A}$$,$${B}$$,$${C}$$とし,$${\texttt{and}}$$を「$${\cdot}$$」,$${\texttt{or}}$$を「$${+}$$」で表すことにすると,最初に述べた4つのケースの考え方は

ですが,分配法則が成り立つことや$${X+\overline{X}}$$が$${1}$$であること,$${X\cdot\text{1}}$$は$${X}$$に等しいことから

であり,他の組合せも同様なので結局

になるということです.
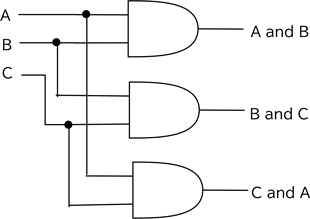
では論理回路に戻りましょう.A and B,B and C,C and Aのどれかが1になっていればいいということになります.
どれかが1になっていれば出力が1になる,というだけであれば下図のようにまとめたいところではあります.

ところが問題文には「入力数が2の回路を用いること」とあるのでこのような入力数3のORは使えません.そこでORを2段重ねにする必要があります.

問2〜問4

NAND回路だけでNOT,AND,ORの回路が作れることを確かめる問題です.まずNOTですが,NOTは入力数が1です.問題文に「入力数が2の回路には同一の入力を与えることもできる」とあるので,NAND回路の入力を1つに束ねてみると,ちょうどいい具合にNOT回路と同じものができます.

つづいてANDですが,これはNANDの出力を反転させることで実現できます.ANDの出力にNOTを追加したのがNANDなのですから,そのNOTをもう1つのNOTで相殺すればいいのです.

最後にORですが,これはすぐには思いつきません.しかし,問題の制約が逆にヒントになります.NANDしか使えないのだから,解答ではNAND回路に何かを付け加えることしかできないのです.NANDの出力にNOTを付け加えることはすでにやりましたから,残っているのはNANDの入力にNOTを付け加えることです.それをやってみると,確かにOR回路と同じものができます(真理値表で確認してください).

このようにその場で考えて試してみることが大事です.
問5

NAND回路だけであらゆる論理回路が作れるので,大量にNAND回路を生産することでコンピュータを完成させることができます.
論理回路の種類
基本的な論理回路は問題で述べられているAND,OR,NOT,NANDのほか,NOR(否定論理和),XOR(排他的論理和,不一致演算)があります.

問題の背景…NANDemoできるNAND回路
NANDやNORの記号はANDやORの出力にNOTを示す丸がついたものです.つまりNANDやNORはANDやORとNOTの組合せで書けるのだから,NANDやNORの記号は必要ないのではないかと思いませんか.
実は論理回路を作るときに使われるFET(電界効果トランジスタ)はNOTのような動作をするので(入力電圧が上がる→FET内を電流が通過する→出力電圧が下がる),NANDやNORの方が単純に作れます.実際ANDやORはNANDやNORの出力にNOTをつけて実装されます.そういった意味で電子回路として基本的なのはANDやORよりもむしろNANDやNORなのです.
また逆にNANDやNORがあればNOTやANDやORは不要である,というのも言い過ぎでしょう.実際,問1を全部NAND回路だけで書くとかなりややこしい回路になりますし,意味も分かりにくくなります.NANDがあればNANDemoできるのは事実ですが,分かりやすさも重要な要素なので極端に走るのはどうかとも思います.
このように「この論理回路だけですべての論理回路が作れる」というものを「完全系」といいます.NANDやNORは1つだけで完全系です.ANDやORやNOTは1つだけでは完全系ではありませんが,ANDとNOT,ORとNOTを組み合わせたものは完全系になります.ではANDとNOTでORを作ったり,ORとNOTでANDを作るにはどうしたらいいでしょうか.もちろんそれは問2〜問4の続きになりますが,もっと簡単にするには……あるいはXORを作るには……これはいい練習問題になるので,実際に考えてみてください.またここで扱った1と0の演算の体系を「ブール代数」といいます.
ところで,この問題では問3,問4でANDとORそれぞれがNANDで作れることについて考えますが,ANDとNOTでORが(あるいはORとNOTでANDが)作れる(数学で習ったド・モルガンの法則から容易に分かります)ことを考えると,この両方を示すのは冗長な感があります.
余談ですが,1ビットの記憶ができるフリップフロップ回路で使われるのも主にNANDゲートです.フラッシュメモリにもNAND型とNOR型がありますが,これの原理はまた別の話になります.
参考文献
1)南山大学: 教科「情報」サンプル問題の掲載について
https://www.nanzan-u.ac.jp/admission/news/2023/240326_joho.html
2)南山大学:教科「情報」サンプル問題の掲載について(7月公開分)
https://www.nanzan-u.ac.jp/admission/news/2024/240719_joho.html
3)大学入試センター:令和7年度試験の問題作成の方向性,試作問題等
https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/r7_kentoujoukyou/r7mondai.html
(2024年6月27日受付)
(2024年7月16日note公開)
■中西 渉(正会員)
名古屋大学理学部卒業後,1989年度から名古屋高等学校教諭(数学科・情報科).情報教育,プログラミング教育が中心.プログラミング学習環境PyPENなどを開発.本会シニア会員.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
