
2022年のあみだくじの問題

山口文彦(長崎県立大学)
連載『教科「情報」の入学試験問題って?』,今回は2022年大学入試共通テスト(本試験)情報関係基礎の第3問をとりあげます $${^{1)}}$$.あみだくじを題材にしたプログラミングの問題です.第3問は,前段があってから,問1,問2,問3が並びます.

ここに引用した前段には,罫線記号(問題文中では単に文字と呼ばれています)を使ってあみだくじを描こうとしているという問題の設定だけでなく,いろいろ重要なことが書かれています.「横線は隣り合う縦線の間のみを結ぶとし,一つの行にはちょうど1本だけ横線があるとした.」と書いてあります.それは「プログラムを簡単にするため」ということですから,プログラムやアルゴリズムを考える上でもヒントになりそうです.また,そうやって描いたあみだくじの一例が図1に示されています.図1が,縦線が3本,横線が4本からなるあみだくじを4行3列に文字を並べて描いた例だということも読み取りましょう.
プログラムでアルゴリズムを表現する
さて問1に入って,プログラムについて具体的に述べられています.

まず,あみだくじを1つ具体的に決めるために必要な情報として,縦線の本数を表す変数tate,各行の横線の位置を格納した配列Yokosen,横線の本数を表す変数yokoが与えられます.【ア】・【イ】・【ウ】は,図1のあみだくじを表そうとしたら,これらの情報がどうなるかについての問で,導入的な問題とも,少し考えさせることで情報の表現への理解を促す問題とも言えるでしょう.前段の図1に例示されているあみだくじに,行番号と列番号を付した図を図-1に示します.このあみだくじには縦線が3本ありますから,【ア】は3です.3行目の横線は2列目と3列目の縦線を結んでいますから,【イ】は2です.4行目の横線は1列目と2列目の縦線を結んでいますから,【ウ】は1です.

もちろん違うあみだくじを描きたいときには,tate,yoko,および配列Yokosenの要素(と要素数)には異なる値が入ります(たまたま同じ値かもしれません).これらの値を適切に指定してやれば,「横線は隣り合う縦線の間のみを結ぶとし,一つの行にはちょうど1本だけ横線がある」という仮定の下であれば,どんなあみだくじでも表現できることも理解できるとよいと思います.

【エ】・【オ】はプログラムの穴埋めです.図2として提示されているプログラムを見ると,

となっています.ここでyokoは横線の本数(つまり表示するあみだくじの行数)ですから,(02)-(13)を「行数のぶんだけ繰り返す」ことはすぐに分かります.その(02)-(13)は,

となっていて,「(02),(03)-(12)で何かをやって,そのあとで改行を表示」しています.これで図1のようなあみだくじが描けるというのですから,(02),(03)-(12) では1行分の表示をしていることを読み取りましょう.その1行分の表示では,(02)でxに1を入れておいて,(03)-(12)では「x ≦ tate の間,」繰り返しています.(04)で【エ】の穴になっている条件で場合分けがありますが,(05)-(07)が実行されるにせよ,(09),(10)が実行されるにせよ,どちらの場合でも,文字を改行なしに表示しています.つまり,提示されている「あみだくじを表示するプログラム」の構造は,「文字の表示を(横方向に)繰り返して1行を表示し,そのあとで改行を表示する」ことを行数のぶんだけ繰り返す,という二重ループになっているわけです.ここでは,あみだくじが1行にちょうどひとつずつ横線を持つと仮定されているので,表示すべき行数は横線の本数に等しくなり,1行の文字数は,あみだくじの縦線の本数に等しくなります.タテとヨコが逆に見えるところが少しややこしい.
繰り返しのためにxとyという2つの変数が登場します.yは上からの行数を表し,xは左から何番目の縦線を描こうとしているかを表していると考えるとよさそうです.あみだくじの1行は「┃」または「┣┫」を並べて描き,縦線の本数が合計でtate本になるわけです.
条件【エ】が成り立ったときに2つの罫線記号を使って「┣┫」と表示し,そうでなければ「┃」を表示しています.つまり【エ】は横線を表示する条件を問う問題です.

横線の位置は配列Yokosenで与えられています.Yokosen[y]がy行目の横線の位置であって,Yokosen[y]番目の縦線とYokosen[y]+1番目の縦線の間に横線を引くことを表しています.「┣」がx番目の縦線(と横線の一部)ですから,Yokosen[y]=xが【エ】の答えです.
横線を描いた後,【オ】を実行してxの繰り返しの次の周回にいきます.横線は「┣」と「┫」の2つの文字で描かれていますので,横線を1本描くと縦線を2本描くことになります.

したがって,【オ】の正解は「xを2増やす」ことを意味するx←x+2となります.
さて1月に行われる試験について,5~6月頃に大学入試センターから報告書が出ています.本稿が皆さんの目にとまるころには,2023年の試験についての報告書が出ているかもしれませんが,本稿執筆時点での最新の報告書が,この2022年の試験のものです $${^{2)}}$$.報告書に,この【オ】に関連して気になる記載があったので紹介したいと思うのですが,その前に,試験問題を分析する方法の一つを解説しておきます:
受験者を総得点の順にいくつかの群(下位層・中位層・上位層など)に分けて,ある問題について群ごとの平均点を求めます(大学入試センターがいくつの群に分けて分析しているかについては,報告書からは読み取れませんでした).もちろん総得点は個々の問題の得点の合計ですから,ある問題の群ごとの平均点と総得点との関係は単調増加になるのが自然です.同じ単調増加であっても,上に凸なら易しい問題,下に凸なら難しい問題,というようにその問題の性質をある程度知ることができます(グラフ-1).

さて,自己評価報告書には「【オ】は問1にありながら正答率の低い難問という結果になった.この設問は成績上位層に続いて下位層の正答率が高く,特に中位層の正答率が低かった.」とあります.つまり,グラフ-2のような単調増加でない結果になったということで,これは異常事態です.
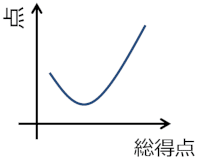
なぜこんな点数分布になってしまったのでしょうか.報告書では「中位層では,『tateを1減らす』や『xを1増やす』との誤答が多かったことから,アルゴリズムを理解することなく『繰り返しの中では変数を1増減するもの』というパターンで回答した受験者が多かったと推測される.」と分析しています.成績上位層の正答率が高いのは当然として,中位層は下位層に比べて問題を解く訓練をされているはずです.教える側・訓練する側としては,正しい訓練を提供できているかどうかが気になるところです.下位層は訓練されていないために,パターンに頼ることができず,結果としてアルゴリズムを考えて回答したことで,正答に至ったのではないかということでしょう.下位層が上位層に次ぐ正答率を得ていたことから,パターンに頼らずに正答することはそこまで難しくないとも思えます.中位層も,アルゴリズムを理解しようとして解けば,もっと高い正答率になったのではないでしょうか.
たしかに,変数を1だけ増減しながらの繰り返しを書くケースは多いのですが,それも増減幅が1である理由があってのことです.この【オ】が現れるのは「x ≦ tate である間,」の繰り返しの中での処理ですから,xを増やすかtateを減らすかしないと繰り返しが止まらないだろうと推測することができます(そして,それは正しい推測です).しかし,だからといって,安直に「tateを1減らせばよい」や「xを1増やせばよい」と考えてはいけないのです.その考え方の中には、あみだくじを描くアルゴリズムが入っていません.このプログラムはあみだくじを描くために書いているのです.報告書は「プログラムは表層的にパターンを組み合わせて作るものではなく,アルゴリズムの表現であるという御指導の徹底を望みたい.」と続いています.図1のプログラムが表している「あみだくじを描くアルゴリズム」は「『文字の表示を繰り返して1行を表示し,そのあとで改行を表示する』ことを行数のぶんだけ繰り返す」という二重ループです.【オ】は(tate文字からなる)1行を表示するという内側のループの中に出てきます.このプログラムでは,2文字描いたら2つ,1文字描いたら1つ,xを増やしてやる必要があることを理解して回答すべき問題なのです.
関数定義でプログラムの見通しを良くする
問2は,あみだくじを引いた結果を求めるプログラムを作ろうというストーリーです.現実にあみだくじを作ったときは,それぞれの選択肢について上端から下端に(もしくはその逆に)ひとつずつたどっていくのでしょうが,そうではなく,すべての選択肢を同時に上から下へたどっていくやり方が最初に説明されています.
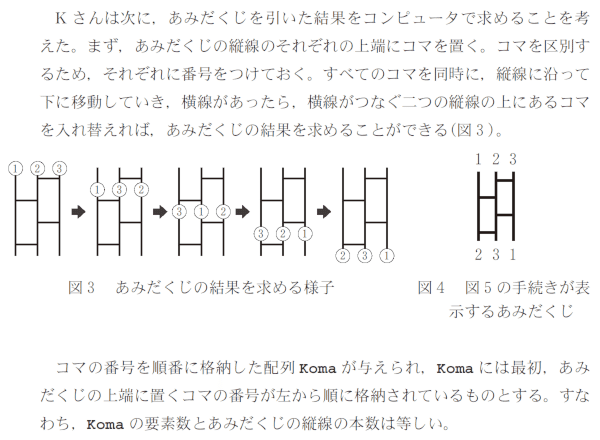
この問題では関数定義が使われています.現在の形式の疑似言語を使うようになってから,関数を定義する形の問題が出題されたのは初めてですし,関数定義の書き方も初めて導入されました.関数と言っても今回は値を返すものではなく,配列の中身を1行に表示するものと,問1のあみだくじを表示するプログラムをそのまま部分プログラムとしたものです.

「あみだくじの結果を求める手続き」として図5に提示されているプログラムでは,最初に「配列を表示する」関数を呼んで最初のコマの並びを表示し,次に「あみだくじを表示する」関数を呼んで,あみだくじを表示しています.(03)~(07)の繰り返しによってあみだくじの結果を求め,最後にもう一度「配列を表示する」関数を呼んで,結果を表示しているというわけです.このように,コマの並びの表示・あみだくじの表示・コマの並べ替え・(並べ替えたあとの)コマの並びの表示,という4つの操作をしているところで,「あみだくじの結果を求める手続き」の本質が「コマの並べ替え」だとすれば,本質的でない部分を簡潔に書けると全体の見通しが良くなります.

さて,【カ】は「あみだくじを表示する」関数を呼び出す際の穴埋めです.図7の関数の定義を見ると,仮引数tateに渡すべき値が問われていると分かります.tateはあみだくじの縦線の本数です.これは,問題文中に「Komaの要素数とあみだくじの縦線の本数は等しい.」 とあるように,要素数(Koma)が正解です.
さて,図5の(03)~(07)の繰り返しによってあみだくじが解けるのですから,ここで図3で説明された何回かの入れ替えが行われるわけです.「何回か」と書きましたが,入れ替えの回数は横線の本数と同じはずです.「yを1から 要素数(Yokosen)まで1ずつ増やしながら,」の繰り返しですから,(04)~(06)で1回分の入れ替えになっていれば,横線の本数だけ入れ替えができると分かります.入れ替えるべきものは配列Komaの隣り合う要素です.【キ】・【ク】 は(04)の代入と合わせて,配列KomaのYokosen[y]番目の要素と,Yokosen[y]+1番目の要素を入れ替える手順を完成させます.

ところで,変数や配列の要素などの記憶装置に覚えている値を入れ替えるには,一方から他方への代入とその逆向きの代入を,ただ続けていっても,うまくいきません.最初の代入で,次に代入すべき値を上書きしてしまうからです.もう一つ別の変数を用意して退避しておくのが常套手段です.ここでは(04)がt←Koma[Yokosen[y]]という代入です.このtが退避用の「別の変数」です.これでKoma[Yokosen[y]]の値を書き換えても,書き換え前の値がtに記録されています.そこで,次の【キ】ではKoma[Yokosen[y]]に Koma[Yokosen[y]+1]を代入します.続く【ク】でKoma[Yokosen[y]+1]にtを代入すれば,入れ替えが完了します.

【ケ】はあみだくじの上下に出力するコマ番号の列を表示する部分プログラムの穴埋めです.ここでは変数jを1ずつ増やす繰り返しをしているので,繰り返す中身がKomaのj番目の要素の表示であればよいわけです.
コンピュータの動作を追いかける
問3は,コマの番号を昇順に並べ替えるあみだくじを作るプログラムが与えられ,その動作を追跡するという問題です. 並べ替えるためには「隣り合う要素の大小関係が逆転しているときに,これらを入れ替えればよい」とだけ説明されています.

プログラムの構造は,変数pとqを使った二重ループになっていて,その内側で,Koma[q]とKoma[q+1]の大小比較をしています.この大小比較が「隣り合う要素の大小関係」を調べていて,昇順にしたいので,Koma[q]が Koma[q+1]よりも大きければ,入れ替えるわけです.この並べ替えの方法はバブルソートなので,このアルゴリズムを知っていれば有利かもしれませんが,問題はこの動作を追跡することですからバブルソートを知らなくても解答可能です.なお,入れ替えと合わせて,どのような入れ替えをしたのかを(問1以来使ってきた)あみだくじの形式で記録するために,配列Yokosenの要素および変数yokoを変化させています.

配列Komaの初期値が[5,2,4,3,1]と与えられています.p=1, q=1のとき, Koma[q]とKoma[q+1]はそれぞれ5と2であって,Koma[q]の方が大きいので,入れ替えが行われます.すると,Komaは[2,5,4,3,1]となって,そのときのqの値がYokosenに記録されるので,Yokosenは[1,0,0,...]となります. Yokosen[1]が1なので、あみだくじの1行目の横線は一番左にあるというわけです.次にqが1増えて,p=1, q=2のとき,Koma[q]とKoma[q+1]はそれぞれ5と4であって,Koma[q]の方が大きいので,やはり入れ替えが行われ,そのときのqの値が横線に記録されるので,Yokosenは,[1,2,0,…]となります.ここまでは表1と図9に示されています.

【コ】~【ス】 は,これに続く配列Komaの変化の様子を答えさせるものです.

p=1, q=2でも入れ替えが行われたのですから,Komaは[2,4,5,3,1]となっていて(【コ】は2が正解),Yokosen[2]が2ですから,あみだくじの2行目の横線は,2列目と3列目の縦線を結びます(【セ】は2が正解).その次は、Komaが[2,4,5,3,1]となっていてqが3の場合です.5は3より大きいので,また入れ替えが行われます.こうして,qを使った繰り返しによって,コマの番号の最大値である5が一番右に行くまで続けて入れ替えが行われます.内側の(qを使った)最初の繰り返しが終わるとKomaは[2,4,3,1,5]となっています.続いて,外側の(pを使った)繰り返しが次の周回に行き,(qの繰り返しがまた最初から始まって)p=2, q=1となります.このとき,2と4を比較しますが,2の方が小さいので、入れ替えは行われません.Komaの要素の並びは変わらないので,【シ】と【ス】は同じになりますし,Yokosenの要素も変わりません.表1で問われている穴埋めはここまでですが,続きをやらないと,図9の穴埋めができません.【セ】~【テ】は,結果として作られるあみだくじを答えさせる問題です.これは表1に記録した配列Yokosenの要素を見れば作ることができます.なお,6個の選択肢がありますが,前段にある仮定から0と5はあり得ないので,実質的には4択です.
問3のここまでの問題は,手間はかかるものの,変数や配列の要素がどう変化していくかを慎重にたどっていけば解けます.途中のケアレスミスが怖い問題とも言えますが,図9には8行あって最上段と最下段に横線が描いてあるので,入れ替えの回数が8回でないか,または最初と最後のどちらかがKoma[1]とKoma[2]の入れ替えになっていなければ,間違いだと分かります.

最後の【ト】は,p番目に大きな値の位置を決めている部分を答えさせるもので,これは上でp=1のときに一番大きな5が一番右まで動いたことからも分かるように,qを使った繰り返しの部分ですから1が正解です.
プログラミングの基礎能力
報告書では第3問について「プログラミングの基礎能力に関する問題である.」としています.今回とりあげた「あみだくじの問題」で測られているであろうプログラミングの基礎能力をまとめてみます.
変数や配列の概念や代入という操作・逐次実行・条件分岐や繰り返しを理解して扱えることはプログラミングの基礎能力に含まれるでしょう.それ以前に,プログラムはアルゴリズム(手順)の表現であるという意識も必要です.正しい意識を持つことも能力のうちと言えるでしょう.代入も条件分岐も繰り返しも、手順を表すために用いられるのです.これは当然の意識だと思えるのですが,試験問題を解く訓練をしていると忘れられてしまうのかもしれません.令和7年(2025年)の試験に向けて対策するのであれば,回り道に思えても,プログラムを書いて動かす勉強をしたらよいのではないかと思います.
関数などの部分プログラムは,少し大きなプログラムを書こうとするときには必須のものです.関数を定義するときにはその中で何をするのかを考えなければなりませんし,関数を使うときには必要な情報を渡してやる必要があります.これらを明確に表現できることは,基礎的能力と言えるでしょう.
プログラムの動作を追いかける能力もプログラムを理解するために基礎的と言えます.プログラムを理解することの重要な面の一つは,そのプログラムを実行したら,コンピュータがどう動くかが分かることです.コンピュータの動作と同じことを,時間がかかろうとも,自分の手でやってみることが,プログラムの理解には必要なのです.
参考文献
1)情報関係基礎 アーカイブ, 情報処理学会 情報入試委員会, https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK
2)令和4年度 問題評価・分析委員会報告書(本試験),大学入試センター,
https://www.dnc.ac.jp/kyotsu/hyouka/r4_hyouka/r4_hyoukahoukokusyo_honshiken.html
(2023年3月20日受付)
(2023年5月1日note公開)
■ 山口文彦(正会員)
長崎県立大学教授.博士(工学).ICPCの日本におけるアジア地区予選審判,パソコン甲子園プログラミング部門審査委員.自動推論・ゲーム情報学・自然言語処理に興味を持つ.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
