
2024年本試験問題 第2問 ついに異星人が地球を訪れた.しかも一度に,トウ星,カイ星,ホク星,リク星という,四つもの星から.

辰己丈夫(放送大学)
今回取り上げるのは,2024年1月に実施された大学入学共通テストの「情報関係基礎」第2問です.この第2問の位置づけなどは,大学入試センターの資料などを見ると分かりますが,手短に書くと「アルゴリズム」や「数量的関係」を重視した問題となっています.2022年からの学習指導要領における「情報I」でも,モデル化とシミュレーションは当然,取り上げられる話題ですから,この問題に取り組んでみることも悪くないでしょう.
この記事では,まず,問題を解く受験生の気持ちになって考えていることを記していきます.その後,この問題の背景などについて説明します.
なお,2024年度の問題は,2024年7月頃に情報処理学会情報入試委員会の情報関係基礎アーカイブに掲載予定です.
解答の作成
まずは背景の説明から
では,早速問題に取り掛かりましょう.

冒頭からいきなり,強く想像力を掻き立てられる書き出しです.異星人がどのような格好なのか,火星人をタコみたいな格好に描いたSF作家は誰だったっけ?などと考えてしまいたくなりますが,そんなことを考えていては,問題に取りかかれません.読み進めましょう.

星の名前は地球で付けたのに,異星人がそれを認知できていて,しかも,返答の「はい」「いいえ」は分かるなど,(SFとして考えると)設定にやや不自然なところはありますが,大事なことは,「宇宙船に乗っている異星人の出身星」を定めることです.
それくらいなら簡単だと思う気を押さえて,ここは,誘導に乗って問題を考えていくことにします.

この表1をよく見ると,宇宙船A,B,C,D,Eで各星の出身者に偏りがあることが分かります.この偏りを利用して,「出身星を早く確定させたい」というのが,この問題の目的だと分かりました.
なので,具体名に惑わされないようにして,この目的を強く意識して,解いていくことにしましょう.
順番に聞くよ

この方法で聞くと,トウ星人については1回で,カイ星人については2回で,ホク星人とリク星人については【ア】= 3回で決まります.
宇宙船Aを想定すると,カイ星人に対しては【イ】= 2人 ✕ 2(回/人)= 4回で,宇宙船Aでの質問回数の合計は3 ✕ 1 + 2 ✕ 2 + 1 ✕ 3 + 4 ✕ 3 = 22回です.
一方で,宇宙船Cを想定すると,質問回数の合計は【ウエ】= 1 ✕ 1 + 3 ✕ 2 + 2 ✕ 3 + 4 ✕ 3 = 25回となります.

この部分は,実際に手計算をすれば求めることができます.カイ星人かどうかを決める質問は1つあとになりますので,【オ】= ④「1回多い」となります.また,宇宙船A全員に聞くときは,表N1のとおりになり,【カ】= ①「2回少ない」となります.

宇宙船Aではリク星出身が4人もいるので,早めに聞き出すことで,質問回数を減らすことができました.
全員2回の質問で決めよう
Mさんは,さらなる工夫を始めました.それが「トウカイ銀河」という分け方です.

この方法だと,どの星の出身であっても,2回の質問で出身星を確定させることができます.ですから,10人なら【キク】= 20回,50人なら100回に固定できます.
一見すると,回数が安定していていいのですが,先程の順次法と比べると,回数が多くなることも生じてしまいます.極端な仮定ですが,ある宇宙船は10人全員がトウ星人であれば,順次法なら10回で確定できますが,グループ法だと20回かかってしまいます.

これは計算をしてみると分かりますね.

宇宙船Aであれば,「リク星?→トウ星?→ほかのどっちか?」と聞けば,質問回数は最小【ケコ】= 19回にすることができます.

単純に計算してみましょう.

以上より,最小となるのは,【サ】= ③ 「宇宙船D」です.しかし,この様子を見ていると分かりますが,出身星が偏っているほど,合計の質問回数は少なくて済んでいます.
さて,どっちをつかうべきなのか?ということでMさんは悩みます.

出身者が2番目に多い星の場合は,順次法でも,グループ法でも2回の質問で確定できます.したがって,順次法とグループ法の違いは,それ以外の星で生じます.グループ法のほうが質問回数が少なくなるのは,1人当りの質問回数が3回となる人数が多いときです.
つまり,「【シ】の人数と【ス】の人数の合計が,【セ】の人数より多い場合」は,
【シ】= ②「出身者が3番目に多い星」の人数と
【ス】= ③「出身者が最も少ない星」の人数の合計が,
【セ】= ⓪ 出身者が最も多い星の人数より多い場合
となります(【シ】と【ス】は入れ替え可能です).
つまり,データの傾向をあらかじめ把握できていれば,順次法とグループ法のどっちがいいのかは分かります.ですが,仮に順次法を利用するとしても,最多の出身星を知ってない状態では,質問の順番を組み立てることはできません.つまり,この2つの方法を比較しても,簡明な「よい方法」は見つからないということになります.
Mさんはグループ法を検討したけど,そのままでは使えないことが分かってしまいました.
グループ法と順次法を組み合わせるよ
そこで,Mさんは,さらなる工夫を考えます.

Mさんの「仮説」は,「最初に調べた宇宙船の構成を前提として,あとの宇宙船を調べる」という方法です.
それは正しいのでしょうか? 今のところは分かりませんが,問題の誘導に乗って進めていきましょう.
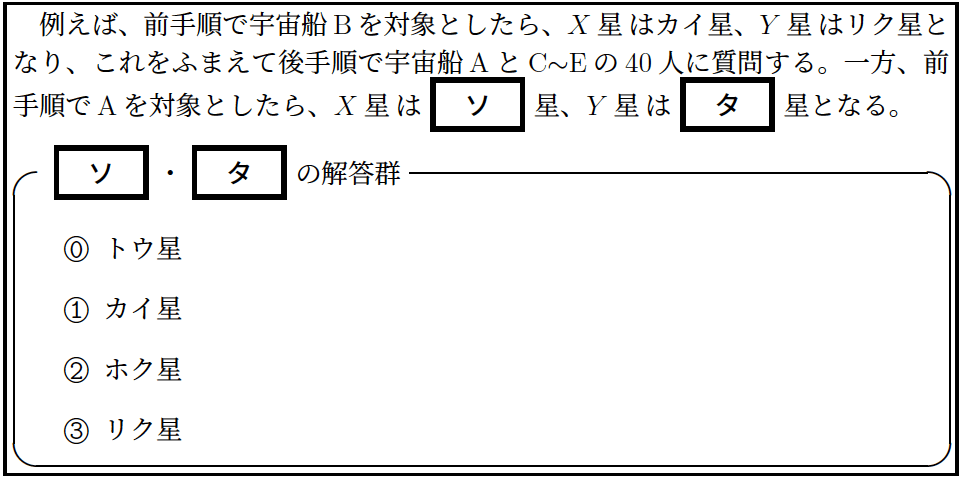
宇宙船Aでは,最多$${\mathit{X}}$$は【ソ】= ③「リク星」で,次$${\mathit{Y}}$$が【タ】= ⓪ 「トウ星」ですね.

この【チツ】を考えてみましょう.宇宙船Bで最多はカイ星です.ですから,宇宙船A,C,D,Eのカイ星出身の人数を加えて,【チツ】= 2 + 3 + 7 + 6 = 18となります.
さて,なぜこのように,前手順で宇宙船Aを採用すると回数が多くなるのでしょう? その考察が続きます.

最後の一文は,

という意味です.もう少し意味をはっきりさせると,

という意味です.省略されているので補って読むしかないです.選択肢を見ましょう.

つまり,リク星が最多である宇宙船はAとCしかなく,一方でカイ星が最多である宇宙船(【テ】= ⓪「$${\mathit{X}}$$星がカイ星となった」船)はB,D,E と3つもあるから,この状況が生じます.
さらに,Mさんは宇宙船Aと宇宙船Cで比較をします.

ここもちょっと読みにくいので補っておきましょう.

空欄が多いのですが,状況を整理し直してみます.
前手順で宇宙船Aを使うと,$${\mathit{X}}$$星はリク星,$${\mathit{Y}}$$星はトウ星
前手順で宇宙船Cを使うと,$${\mathit{X}}$$星はリク星,$${\mathit{Y}}$$星はカイ星
です.上記の整理から,【ナ】= 「② $${\mathit{Y}}$$星 がカイ星となった」は簡単に分かりますが,【ト】は,少し意味不明ですね.選択肢を見てみましょう.

宇宙船Aと宇宙船Cのどちらでも$${\mathit{X}}$$星はリク星で,どちらも4人ずつですから,後手順での影響はありません.したがって, ⓪と①は正解ではありません.②と③を比較して宇宙船Cのことを述べている選択肢を探します.
「その他」という言葉が,「何のその他」なのかが明示されてませんが,表2を見て「$${\mathit{X}}$$星でも,$${\mathit{Y}}$$星でもない,他の2つの星」と解釈するという発見ができるなら,次の結果を発見できます.
宇宙船Aでは,その他(カイ星,ホク星)は 7 + 3 + 7 + 6 + 1 + 2 = 26 人
宇宙船Cでは,その他(トウ星,ホク星)は 3 + 1 + 1 + 1 = 6 人
このことから,【ト】= ③「後手順でその他が少なかった」が正解と分かります.

これは前手順で宇宙船Bを対象としたときと,前手順で宇宙船Eを対象としたときを比較して考えます.


表N2と表N3を比較してみると,前手順で見る宇宙船を宇宙船Bから宇宙船Eに変更すると,後手順の$${\mathit{X}}$$星人の人数が18人から19人に増える代わりに,$${\mathit{Y}}$$星人の人数が14人から13人に減ります.$${\mathit{Y}}$$星人であると判断するには2回の質問が必要なので,結果として,質問回数を減らすことができるのです.
しかし,選択肢には,「前手順と人数の関係」のことしか書かれていません.前手順と後手順の関係は何でしょう?
前手順で宇宙船Eを見ることにすると,前手順で$${\mathit{X}}$$星人が1人少なくなり,その分,後手順で$${\mathit{X}}$$星人が1人増えます.順序を変えると変化が現れるのは後手順の方ですから,結果として前手順で宇宙船Eを見る方が【ニ】 = ①「前手順でX星人が少なかった」となり,質問回数が減るということになります.
以上で,問題は終わりました.お疲れさまでした.
解説
さて,この問題,ひたすら計算ばかりさせているのですが,背景となる項目があります.
決定木
データを見て,何かを決定する過程を図示する方法の1つとして,決定木と呼ばれる方法があります.
次の図1と図2は,本問における異星人への質問を通して,出身星を決める決定木の例です.


これらの決定木を見ると,順次法では質問回数が一定でないのに対して,グループ法では一定回数で決まることが,簡単に分かります.また,少ない質問回数で終わる対象が多ければ多いほど,全体の質問回数が下がることもすぐに分かるでしょう.
バックテスト
問1では,「Mさんは,これからやってくる異星人の出身星を決める最もよい方法は分からないけど,それでも,一定の方法を決めて,過去の実績に基づいて分析できるかどうか」を確認しようとしていました.
この方法は,気象データを前提とした対策や,少額の為替投資・株式投資などで戦略を考えるときに用いられるバックテストと呼ばれる手法です.
Mさんが方針を決めても決めてなくても,相手(気象データ,為替レート,株価,異星人の比率)が変わることはありません.だから,過去の記録を前提にして,方針をいろいろと思案(変更)して,良い結果に至る方針を追求していくのです.
一方で,為替や株式取引でも,非常に金額が大きい場合は価格に変動が生じるため,完全なバックテストはできません.また,囲碁・将棋・チェスなどのゲームや,野球やサッカーなどの相手がいるスポーツ競技等の場合は,こちらの方針・戦略によって相手の対応・動向が変わりますので,バックテストを行うことはできません.
暗黙の前提?
問2では,
トウ星とカイ星はトウカイ銀河にある
ということを知ったMさんがグループ法を思いついて,バックテストをしました.
しかし,ひょっとすると,ホク星やリク星のどちらか,あるいは両方ともトウカイ銀河にあるかもしれません.Mさんは,このことに気が付くことができるでしょうか?
仮に4つの星がすべてトウカイ銀河にあったとしましょう.そして,未来に異星人が,これらの4つの星からやってきます.このときにMさんがグループ法で聞いてみると,すべての異星人が「トウカイ銀河から来ましたか?」という質問に「はい」と返答するでしょう.そのとき,Mさんは,「このグループ法ではうまくできない」ことに気が付き,分析手法を再検討することになります.
本問題では,手法を検討しているバックテストなので,ここは不問にされていて,
ホク星とリク星はトウカイ銀河にない
という「暗黙の前提」をしています.
他に,問3で

という意味の文章を

と省略しています.同様の省略は,この後にも複数の個所で出現しています.この点は,出題者が正確に書こうとしたが紙面の都合で省略してしまったのかもしれません.日常会話では,こういうぶっきらぼうな言い方はよくあることですが,ここでは問題文に現れました.考える際には,補って読むことも求められています.
分布の推定
本問のように,分布の状況によって計算回数などが異なる手順(アルゴリズム)があったとき,その回数を少なくするために,分布をあらかじめ調べる,という方法が有効です.
本問の場合は,単に,出身星を数えるだけです.この場合は,一部を標本として利用し,全体を調べることにつかうことが一般的です.標本次第では運が悪い状況が発生して,全体として手間が多くなる結果になるかもしれません.現実に用いられるアルゴリズムでは,この点でも工夫がなされています.
また,本問よりもさらに高度な処理を行うにあたり,データ全体を一度読み込んで,そのあとに,方針を判断して,あらためて情報処理を行うことも考えられます.たとえば,圧縮アルゴリズムの一つであるハフマン法では,想定(仮定)した各データの出現比率を利用して,符号化します.
なお,本文ではハフマン法のことを知っていると,ちょっとだけ楽に解くことはできますが,「頻度が多い項目から聞き出す」というのは,そんなに難しいことではありません.「先取り学習をしている人は有利」という状況には,ほぼ該当しないと分析できます.
近年,改良がめざましい人工知能ですが,機械学習を行う際にも,この「分布の推定」が行われています.学習データを前提にして作った方針が,分布を上手に推定できるようになれば,より現実味のある文章,絵画などを生成できるようになってきます.
参考文献
1)情報処理学会 情報入試委員会:情報関係基礎 アーカイブ,
https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK
(2024年4月2日受付)
(2024年5月9日note公開)
■辰己丈夫(正会員)
1991年早稲田大学理工学部数学科卒業.2014年筑波大学博士(システムズ・マネジメント).1993年早稲田大学情報科学研究教育センター助手.その後,神戸大学.東京農工大学を経て,現在,放送大学教授.2020年より2年間,本会理事(新世代).本会広報広聴戦略委員会副委員長.ほかに,教科書委員会,会誌編集委員会,初等中等教育委員会,一般情報教育委員会など各委員.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
