
【書評】 圏論的量子力学入門
ここ1、2年ほど、本業の合間を縫って量子論の勉強に趣味の時間を充てている。最近、ようやく『圏論的量子力学入門』(ボブ・クック、アレクス・キッシンジャー共著、川辺治之訳)を完読し、その内容に深く感銘を受けたので、余韻冷めやらぬうちにこの本の感想を書き記そうと思う。
はじめに(圏論的量子力学について)
「圏論的量子力学」 とは、文字通り、数学基礎論の「圏論」を用いて量子力学の数学的構造を解明する学問分野だ。この分野は比較的新しく、ここ
20年ほどで急速な発展を遂げている。しかし、本書では圏論の話はそれほど多くは登場せず、学部1〜2年程度の量子論と線形代数の基礎知識があれば、圏論を全く知らなくても読める内容となっている。その理由は、この約900ページの大著のほとんどが「ストリング図式」と呼ばれる「箱と結線の絵」で埋め尽くされており、かつ一つ一つの図式(の証明)の解説が非常に丁寧だからだ。そのため、本書を読み進めるのは、まるで絵本をゆっくり読み聞かされているような感覚に近く、ディラックのブラケットやテンソル記号等で埋め尽くされた難解な数式を見て気絶する人(私)にとっての福音書となる。また、本の後半に入ると、ストリング図式をさらに拡張した「スパイダー(多肢点)図式」と「ZX図式」が登場する。箱の中身を「位相情報をもつ節点」に分解し、量子論の重要な性質の一つである「相補性」を2色で表現するので、よりシンプルでカラフルな図式が楽しめる。
ちなみに原著は「Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning」。表紙には謎めいたドードー鳥と量子テレポーテーションのイラストが飾られ、タイトルに圏論の文字が無いなど、和訳書と比べてより親しみやすい印象を与えている反面、著者が提唱する「量子描図主義」の本気度があまり伝わってこないのが、ギャップがあって面白い。
なお、本書は物理学の「量子力学」よりも情報科学の「量子情報」に分類される。量子力学の歴史的背景については、ヤングの二重スリット実験やシュテルン=ゲルラッハの実験といった定番の話題に留まっており、物理学の歴史と発展のロマンを味わいたい人にとっては、今一つ刺さらないかもしれない。一方、圏論にまだ触れたことのない理論家にとっては、数式を使わず図式のみでこれらの実験内容をあっさりと説明できてしまう切れ味の鋭さに、きっと舌を巻くだろう。いずれにしても、従来の量子力学で培ってきた知見を一旦脇におき、全く新しい量子情報の書物として読み進めることをお勧めする。読み解いていくうちに、「従来の量子力学」と「圏論的量子力学」の見事な対応関係が浮かび上がってくるはずだ。
ストリング図式
『圏論的量子力学入門』では、従来の数式を使った量子論に代わって「ストリング図式」が中心的な役割を果たす。ストリング図式とは、圏論における「モノイダル圏」を視覚的に表現し、テンソル積による複合系を扱うための思考のフレームワークを提供するもので、さまざまなプロセス理論に幅広く応用できる。もし、読者がホワイトボードなどで、下図のような何らかのフローチャートや関係図を描いた経験があるなら、無意識のうちに既にストリング図式を使っていた可能性がある。
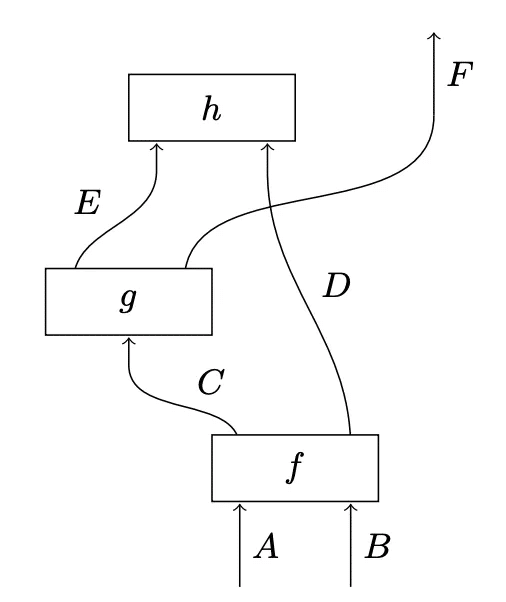
本書では、(圏論的な意味での)ストリング図式を「回路図式」「一般図式」「(本書で言う)ストリング図式」に細かく分類している。圏論では、それぞれ「ストリクト対称モノイダル圏」「トレース付きストリクト対称モノイダル圏」「ダガーコンパクト(対称モノイダル)閉圏」という呼び名があり、後者になるほど図式が強力になる。
例えば、回路図式は電子回路のようなもので、同じゲートの入力と出力をつなげてしまうとフィードバックループが発生し、場合によってはゲートが破損する危険性を伴う。あるいはプログラミングでは、関数の出力を同じ関数に再度入力することで、停止しないかもしれない再帰を生み出す。どちらの場合も、ループを許すと世界が暴走する(=矛盾を起こす)場合が存在する。
この考えを、物事の時系列の世界にも同じように当てはめることができる。一度起きた出来事は、時間を遡って同じ時刻・同じ出来事のまま何度も起こらないのが正常と言える。つまり時系列は因果関係に従い、時間の矢は一方向を進むのみで、フィクション映画のようにタイムリープを起こさない。これは、私たちの常識の範囲内にある。
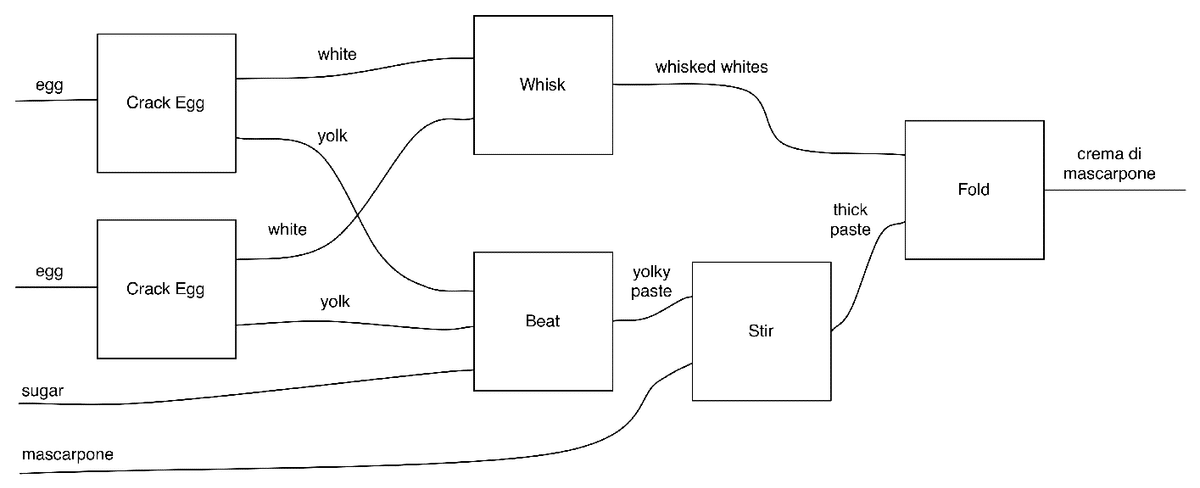
なお、この図式を数式(またはプログラミング風)で書くと、
(crack ⊗ crack ⊗ id) ▹ (id ⊗ swap ⊗ id) ▹ (whisk ⊗ beat ⊗ id) ▹ (id ⊗ stir) ▹ fold
出典:Crema di Mascarpone and Diagrammatic Reasoning | Graphical Linear Algebra
ところが、量子論ではボルン則に従い、行列のトレースを計算することが可能なため、あたかも時間を遡るかのように、図式上において出来事自身へのループ構造を許容する(一般図式)。この自己ループの概念をさらに強力に推し進めると、「他の出来事と自由につながり合う(入力と入力、出力と出力が絡み合う)」ことすら可能となり、量子の世界の因果関係が破綻する(ストリング図式のコンパクトの性質による)。これがいわゆる「量子もつれ(絡み合い)」 やその応用の「量子テレポーテーション」といった、従来の常識では考えられなかった新しい物理学の理論・計算体系の確立へとつながっている。

Alice-Bob間の量子的に絡み合ったベル状態を利用して、量子状態を瞬時に転送可能にする。
(ただし、BobはAliceから古典情報を別途受け取るまで、補正 f について何も分からない)
ストリング図式の二重化
本書の最初の見どころは第6章にある、古典的な確率統計的体系から量子の非決定的体系に移行するにあたって、古典論で使えるストリング図式を二重化して量子論でも扱えるようにした点になるだろう。かつてフォン・ノイマンが量子力学を形式化するにあたって密度演算子や射影演算子を導入したことを圏論化したものに相当するが、これにより量子の世界についても、ストリング図式の性質を保ちながら視覚的に操作できるようになった。
本書ではまず、古典的な「線形写像の圏」を起点に、線形写像の二重化による「純粋量子写像の圏」を構成する。ここで二重化とは、元の線形写像の共役を取り、2つの写像を並列に並べること意味する。純粋量子写像の圏では、それらを束ねて1つの写像とみなし、その圏もまたストリング図式の性質を満たす。ただし、この過程を経て「古典的振る舞いをそのまま量子の世界に移植できる」わけではないので注意。例えば、古典複製写像を二重化したところで、任意の量子状態を複製する(純粋)量子写像は作れない(量子複製不可能定理)。
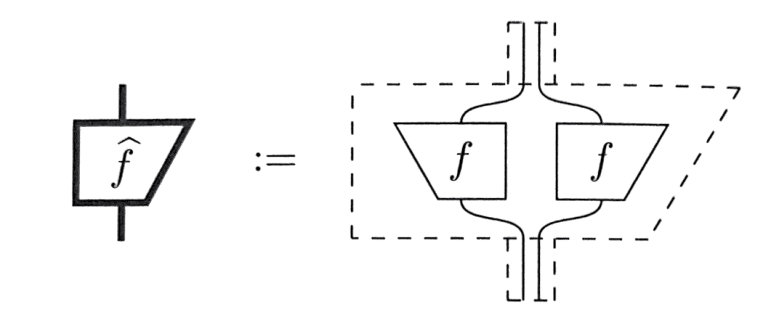
線形写像 f が二重化されたものを1つの写像 f^ にまとめる。
この二重化の後、廃棄エフェクトを導入して、より一般的で混合可能な「量子写像の圏」に拡張する。廃棄とは、二重化で表現できない量子効果であり、量子系の一部を無視することに相当する。ここで、量子写像(⊗正値写像)の形を少しばかり変形すると、簡単にクラウス表現$${Φ(ρ)=Σ_iK_iρK_i^†}$$が得られる。したがってチョイの定理より、量子写像とはCP(完全正値)写像のことで、量子状態の部分系にのみ量子写像を適用しても、系全体として量子状態の性質(⊗正値)を保つ。
さらに量子非決定性を付与すると「量子プロセスの圏」へと発展していく。第6章の段階ではまだ複雑な仮の非決定性図式を用いているが、この時点でも十分に、量子テレポーテーションの大まかな流れが理解できるようになる。
それから第7章の「量子測定」(正規直交基底による測定、射影測定、POVM)を経て、量子系と古典系の橋渡しの仕組みを理解した後、第8章で「スパイダー(多肢点)」とその図式によって非決定性の複雑さを刷新。量子測定とデコヒーレンスの概念を含めた「古典・量子写像の圏」へと拡張される。
スパイダー(多肢点)図式
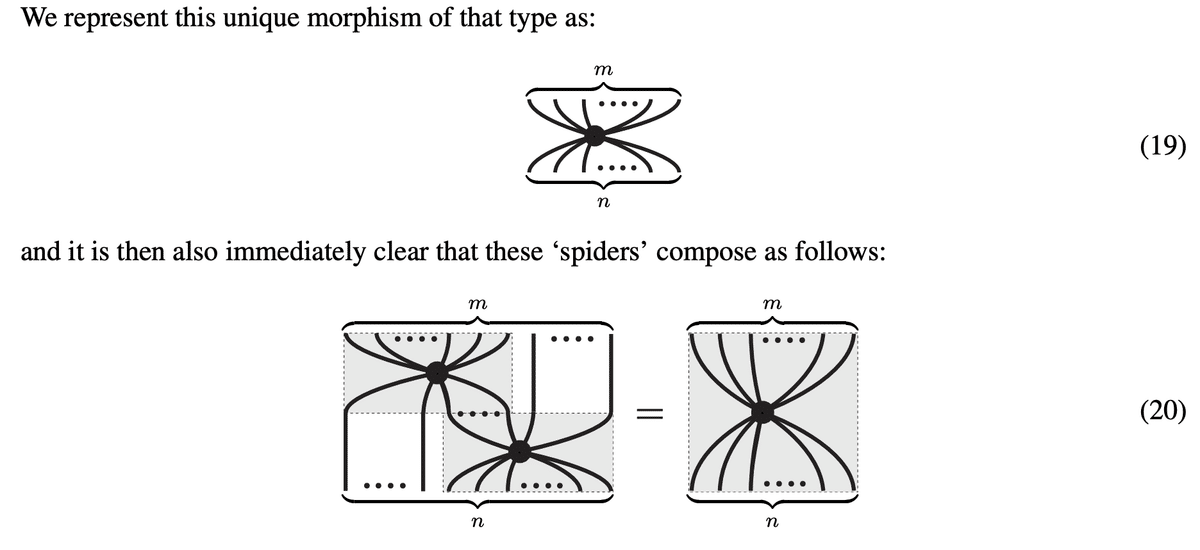
スパイダー(多肢点)は、上図の通り、蜘蛛の形をした任意の本数の足を持つ節点であり、その定義は「巨大なクロネッカーのデルタ記号(多変数版)」である。言い換えれば、スパイダー内部の各正規直交基底(状態とエフェクト)がすべてシンクロしながら、その和を取る。例えば、単位の分解 $${\sum_{i,j} \delta_{ij} |i\rangle \langle j| = 1}$$ や複製 $${\sum_{i,j,k} \delta_{ijk} |ij\rangle \langle k|}$$ 、XOR演算 $${\sum_{i,j,k} \delta_{ijk} |i\rangle \langle jk|}$$ などがその具体例となる。数学では 「フロベニウス多元環」と呼ばれ、モノイドとコモノイドの両方の性質を併せ持ちながらフロベニウス則を満たす。この話をさらに発展させると、「ダガー特殊対称フロベニウス多元環(C*環と同型)」が得られ、スパイダーの基本操作で重要な「融合則」のルール等が図式計算に組み込まれるようになる。融合則によって、図式中に大量発生したスパイダーの数を減らして、図式を簡略化することができる。
ここでスパイダーには、量子の世界の二重結線のみで結ばれている「二重化された量子スパイダー」と、古典的結線を一部に含む「一重の古典スパイダー」の2種類が存在する。そして、融合則が「古典スパイダーを好む」ことに留意する。つまり、図式中に一度古典スパイダーが混じると、結線でつながった(量子の良い性質を持つ)周辺の量子スパイダーはその古典化(量子測定やデコヒーレンス)に巻き込まれ、存在しなかったものとみなされる。言い換えれば、波動関数の収縮が起こり、古典情報が取り出されたり無視(=古典的削除)されることを意味する。

なお、この古典情報は量子情報とは異なり、光の速さを超えて瞬間伝送することはできないため、アインシュタインの相対性理論および時間の因果律は保たれる。そのため、前述の量子テレポーテーションの図を総合的に見れば、補正 $${f_i}$$ を伝えるためにその古典情報 $${i}$$ を別途転送する必要があり、結果的に(古典)情報を瞬時に共有できないと結論付けられる。
多色位相スパイダー図式
第9章では、スパイダーをさらに改良した「位相付きスパイダー」「色付きスパイダー」について詳しく解説されている。前者については、スパイダー図式に相対位相の概念が加わると位相が可換群をなすことから、量子スパイダーの融合時に位相の和が生じるようになる。また後者は、量子の相補性が加わることで、スパイダーに色を付けて分別することができる。
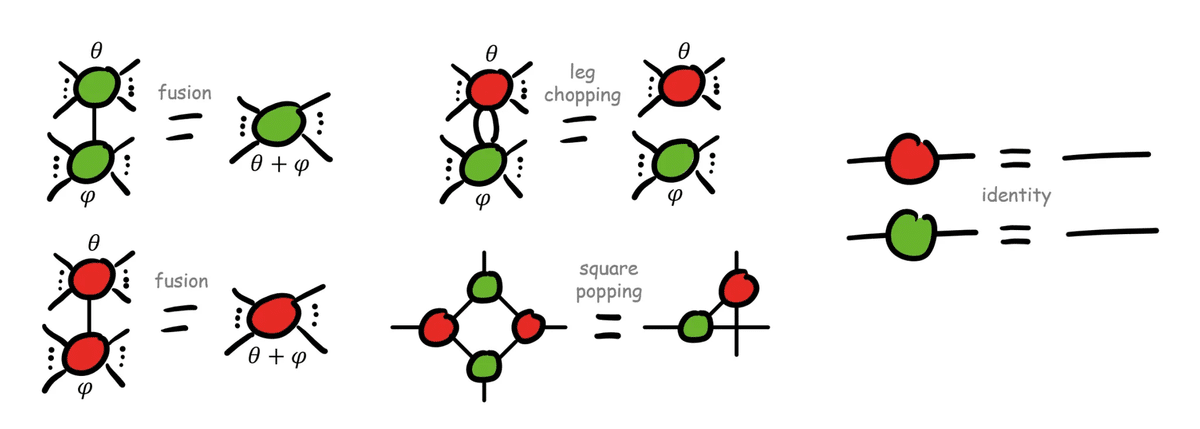
出典:Quantum Picturalism: Learning Quantum Theory in High School | Abstract
興味深いのは、「色の異なる相補的な2匹のスパイダーが2本の結線で結ばれているとき、それらの結線を無いものとみなせる」という性質だ。これは相補性の定義であり、その数学的背景としてホップ代数がある。相補的な2色を選ぶにあたり、自己共役な正規直交基底(例:ブロッホ球のZ軸方向とX軸方向)を選ぶことで、ホップ代数の対合射は恒等射になる。また、ホップ代数の親クラスである双代数(これもまたモノイドとコモノイドの両方の性質を併せ持つ)の規則が図式計算に持ち込まれる(強相補性)。
そして、スパイダーとその相補的性質が分かるようになると、いよいよ「シュテルン=ゲルラッハの実験」や「量子暗号通信」、「量子的非局所性」などの仕組みについて、数式を使わず図式のみで解釈できるようになる(ただし位相が登場しているので、簡単な足し算の暗算は必要)。これでようやく、原著表紙のスパイダーを使った量子テレポーテーションの図式も読めるようになり、晴れてドードー鳥と肩を並べられる。
ZX図式
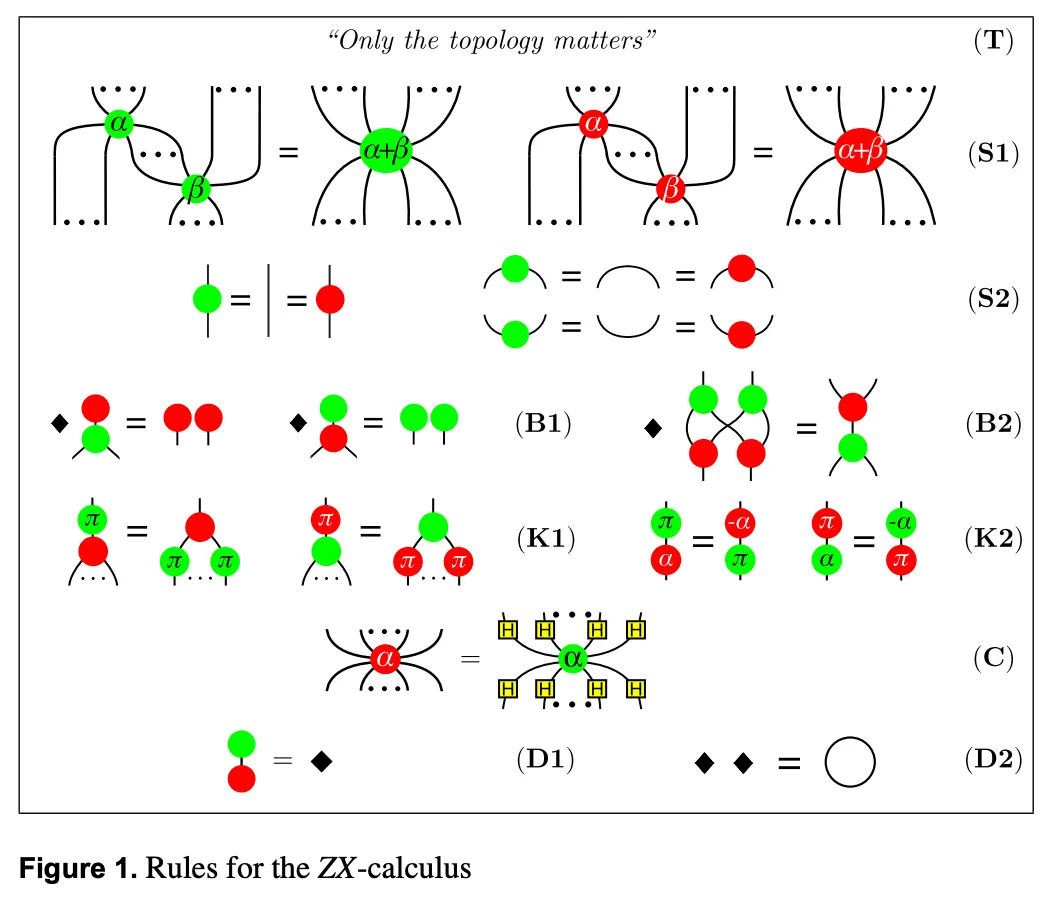
ZX図式は、前節の多色位相スパイダー図式の量子系を1量子ビット(2つの複素数 $${ℂ^2}$$)においたもので、2色の位相スパイダー(位相ゲート)と量子CNOTゲートから、任意個の量子ビットの量子回路を作ることができる。本書では、位相を $${π/2}$$ の整数倍に限定したクリフォード図式(古典論のシミュレートが可能)や、クリフォード+T図式(位相を $${π/4}$$ の整数倍に限定)について紹介している。
また、ZX図式は量子アルゴリズムを読み解く道具としても役立つ。本書では、相補性を用いた任意の関数のユニタリ化「量子オラクル」を用いた、ドイチェ-ショザのアルゴリズム、量子探索、隠れ部分群問題を取り上げている。
本書の感想
本書では上記以外にも、ストリング図式の基礎、線形代数への応用、古典論理ゲート、関係(の圏)、ヒルベルト空間などについて一から丁寧に解説しており、初学者に配慮した、非常に良く練られた構成となっている。それだけでなく、圏論の抽象的な話を本筋から巧みに切り離し、読者に負担をかけないようにする著者の技量も光っている。本記事の紹介も、そのアプローチに倣うべきだったかもしれない。
個人的に、特に感動した点や嬉しかった点は、以下の通り:
大学で学んだ密度演算子やクラウス表現などが、量子写像(二重化と廃棄)の図式で表現できる
大学で学んだ単位の分解が、プログラミングでもおなじみの COPY や XOR に密接に関係し、巨大デルタ記号のスパイダーに一般化できる
大学で学んだシュテルン=ゲルラッハの実験が、スパイダー図式を使って簡単に示せる
量子テレポーテーションや量子暗号通信などの先駆的な技術の仕組みについて、専門家でなくても理解できる
このように並べてみると、感動とは全く新しい概念(私にとっての量子アルゴリズムなど)単体からというより、既知の概念との意外な結びつきから生まれることの方が多いと改めて認識させられる。
まとめ
冒頭にも書いた通り、『圏論的量子力学入門』は、従来の数式中心のアプローチから脱却し、図式を多用した革新的な量子論の名著である。丁寧な解説も相まって、大学1〜2年レベルの線形代数と量子論の基礎知識があれば、本の内容を理解することができる。
唯一の難点は、値段が13,200円と高額な価格設定であること。だが、その内容の量と質を考慮すれば、十分に投資する価値がある。興味を持った読者にはぜひ shut up and take my money の精神で一読をお勧めしたい。個人的に、これまで読んできた量子論の本の中で、最も衝撃を受けた一冊である。
参考文献
本ブログで紹介した「スパイダー図式」の話をより簡単にまとめた『お絵かき量子論』が、同じ著者から出版されている(英語になるが、Kindle版は値段的にもお求めやすい)。
本書よりもさらに数学色を強めた書籍はこちら(良書だが、先にドードー鳥を買うことを個人的にお勧め):
最後に、初学者向けのストリング図式の入門と線形代数への応用については、インターネット上に多くの記事があり、例えば下記が参考になる。
