図式で学ぶ線形代数 #1 ～図式の基礎と線形代数の基礎～

連載の記事一覧：
#1 図式の基礎と線形代数の基礎
#2 スペクトル分解と特異値分解
#3 テンソル積およびトレース・転置・内積
#4 行列が作るヒルベルト空間
番外編 列ベクトルや行列での微分
番外編その2 ベクトル解析

---

はじめに

書籍「図式と操作的確率論による量子論」を22年10月に出版する予定です。本書の紹介を兼ねて，量子論を学ぶ際に役立つ線形代数の基礎を数回に分けて紹介したいと思います。線形代数に対して広く使える内容になっていますので，量子論に興味がない人にも役立つと思います。

Kenji Nakahira - 図式

この連載では，図式を活用することで線形代数の基礎のいくつかをわかりやすく説明することを目的とします。図式とは，数式の代わりに図形を用いて表現した式のことです。線形代数に関する多くの数式は図式により厳密に表すことができ，しばしば数式よりも直観的に理解しやすく楽に計算できるという利点があります（数式のほうがわかりやすい場合もありますので，使い分けるとよいと思います）。これから紹介する図式は，量子回路やテンソルネットワークなどとの相性もよいです。この連載を通して，図式の威力や面白さなどが伝わればと考えています。

この連載の対象読者としては，図式を用いて線形代数を直観的に理解したい方を想定しています。線形代数に詳しくなくても構いませんが，一度は線形代数を学んだことがある方を対象とします（例えば「ベクトル」や「行列」を一度も聞いたことがない方にとっては難しいと思います）。すでに線形代数の基礎を習得していて図式にのみ興味がある読者は，興味のある箇所のみを拾い読みしていただけると幸いです。なお，話を簡単にするため無限次元空間は扱いません。

図式の基礎と線形代数の基礎

以下 ，スライドを示した後，文章でスライドを補足するようなスタイルで説明します。スライドに目を通してから文章を読むとわかりやすいと思います。

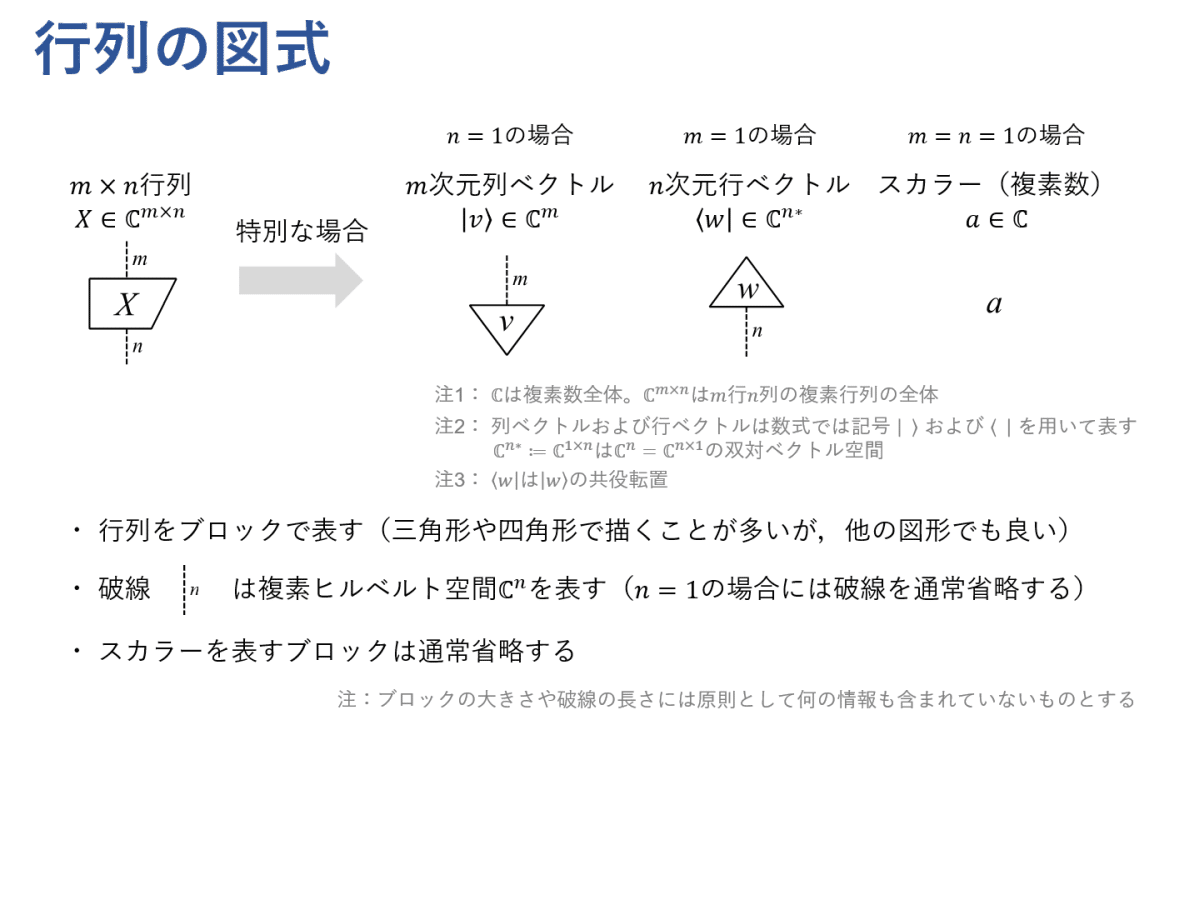
図式では，行列をブロックで表してヒルベルト空間を破線で表すことにします。この記事では量子論を意識して $${\Complex^n}$$ のような複素ヒルベルト空間を考えますが，これから述べる内容の大半は $${\R^n}$$ のような実ヒルベルト空間に置き換えてもそのまま成り立ちます。なお，ヒルベルト空間とはベクトル空間のことだと考えてもらって構いません（詳細は省きますが，$${\Complex^n}$$ または $${\R^n}$$ を考える限りこれらの本質的な違いはないといえます）。

列ベクトルや行ベクトルや複素数（スカラーとよびます）は，行列の特別な場合とみなせます。例えば，$${n}$$ 次元列ベクトルは $${n}$$ 行 $${1}$$ 列の行列とみなせます。なお，$${\ket{v}}$$ のような列ベクトルはケットベクトル，$${\bra{w}}$$ のような行ベクトルはブラベクトルとよばれます。

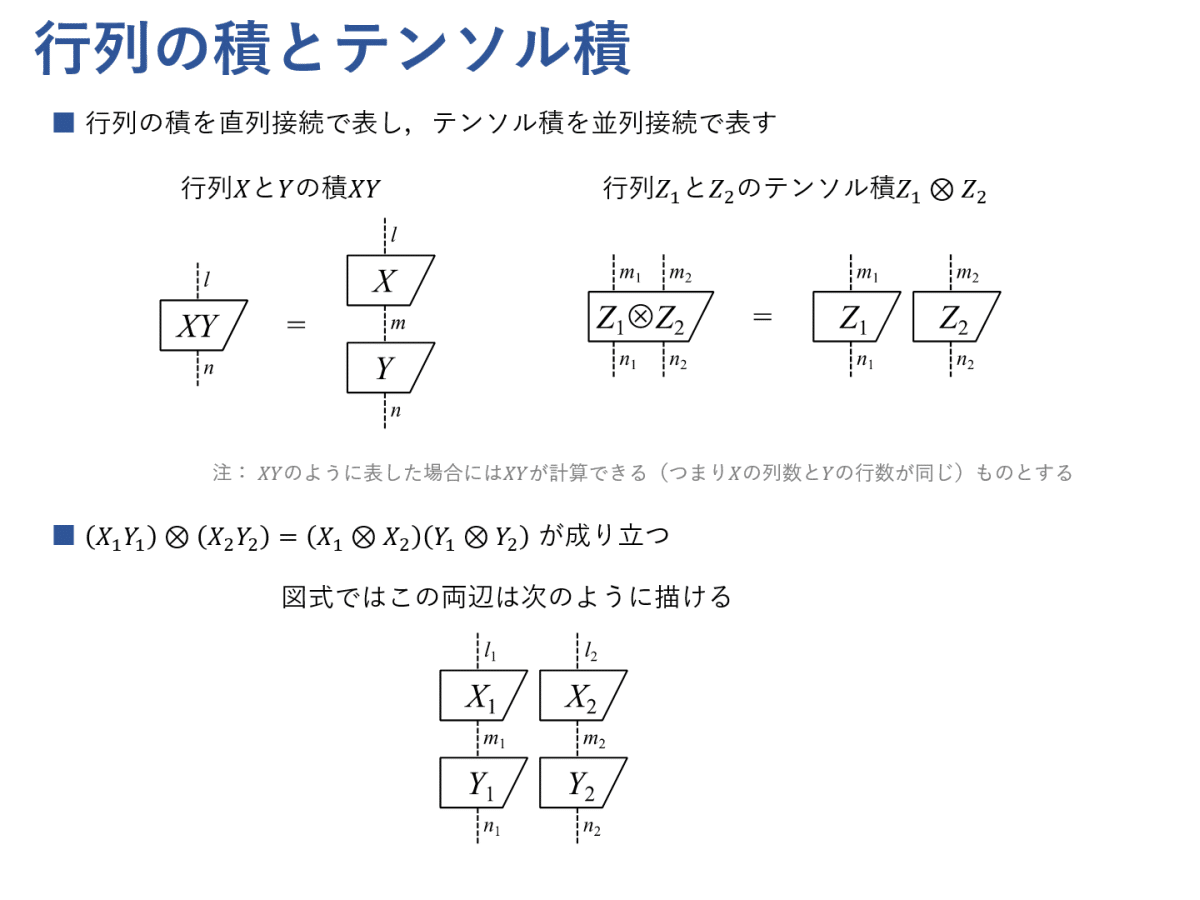
図式では，行列の積およびテンソル積を，それぞれブロックの直列接続および並列接続で表します。直列接続では，同じラベルの破線同士のみを接続できることとします。これは，行列の積 $${XY}$$ が $${X}$$ の列数と $${Y}$$ の行数が同じである場合にのみ計算できることに対応します。

テンソル積を記号 $${\otimes}$$ を使って表します。なお，テンソル積について知らない方は，ひとまず「並列接続に相当するもの」といった理解で十分です。

各ブロックは，そのブロックの下側の線から入ってきた情報を処理して上側の線に出す（つまりブロックの下側が入力で上側が出力）ような写像であると考えるとわかりやすいと思います。$${XY}$$ は「$${Y}$$ を施してから $${X}$$ を施すような写像」（つまり写像の合成）とみなせます。

スライドの下にある図式から，「2個の直列接続 $${X_1Y_1}$$ と $${X_2Y_2}$$ の並列接続」（つまり $${(X_1Y_1) \otimes (X_2Y_2)}$$）は「2個の並列接続 $${X_1 \otimes X_2}$$ と $${Y_1 \otimes Y_2}$$ の直列接続」（つまり $${(X_1 \otimes X_2) (Y_1 \otimes Y_2)}$$）に等しいことが直観的にわかると思います。直列接続を「逐次処理」，並列接続を「並列処理」と解釈するとイメージをつかみやすいかもしれません。

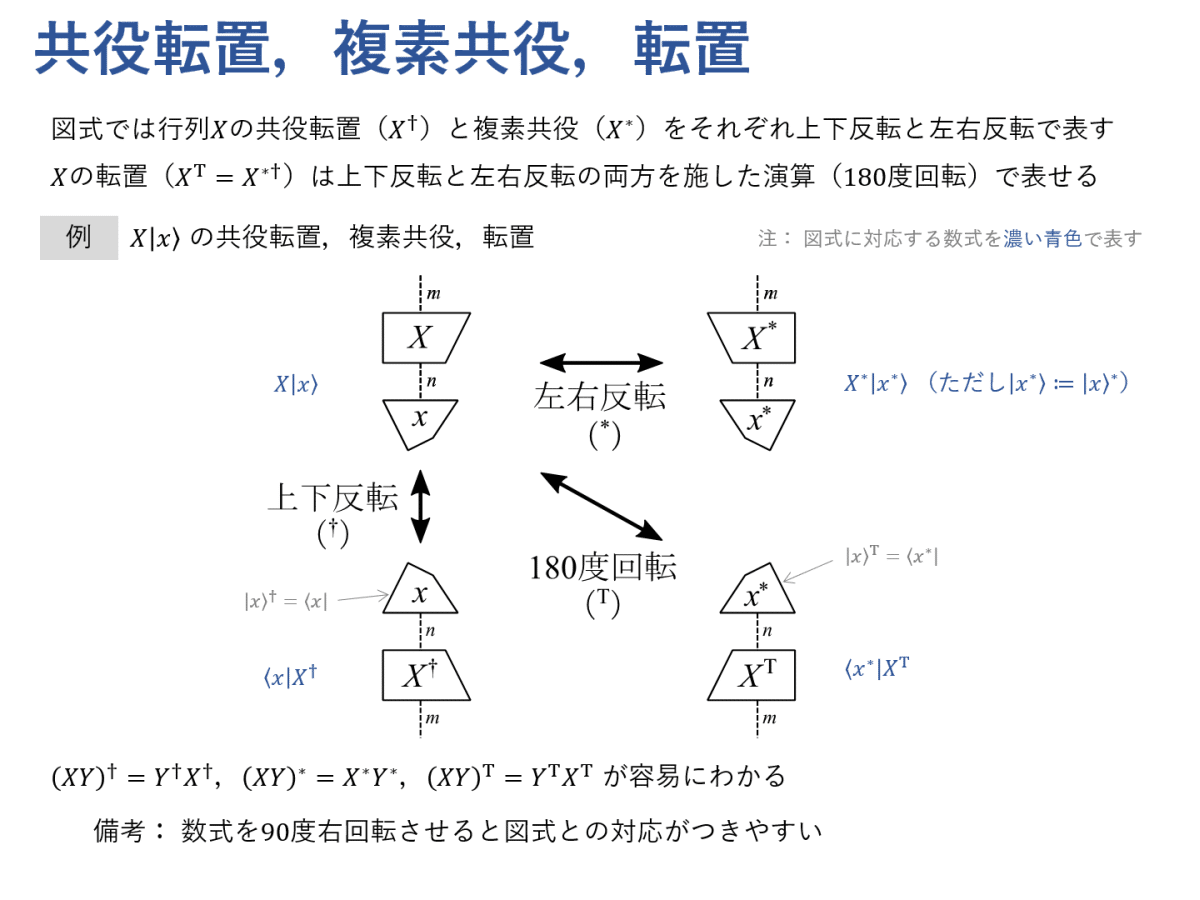
共役転置と複素共役は，図式ではそれぞれ上下反転と左右反転で表すことにします。

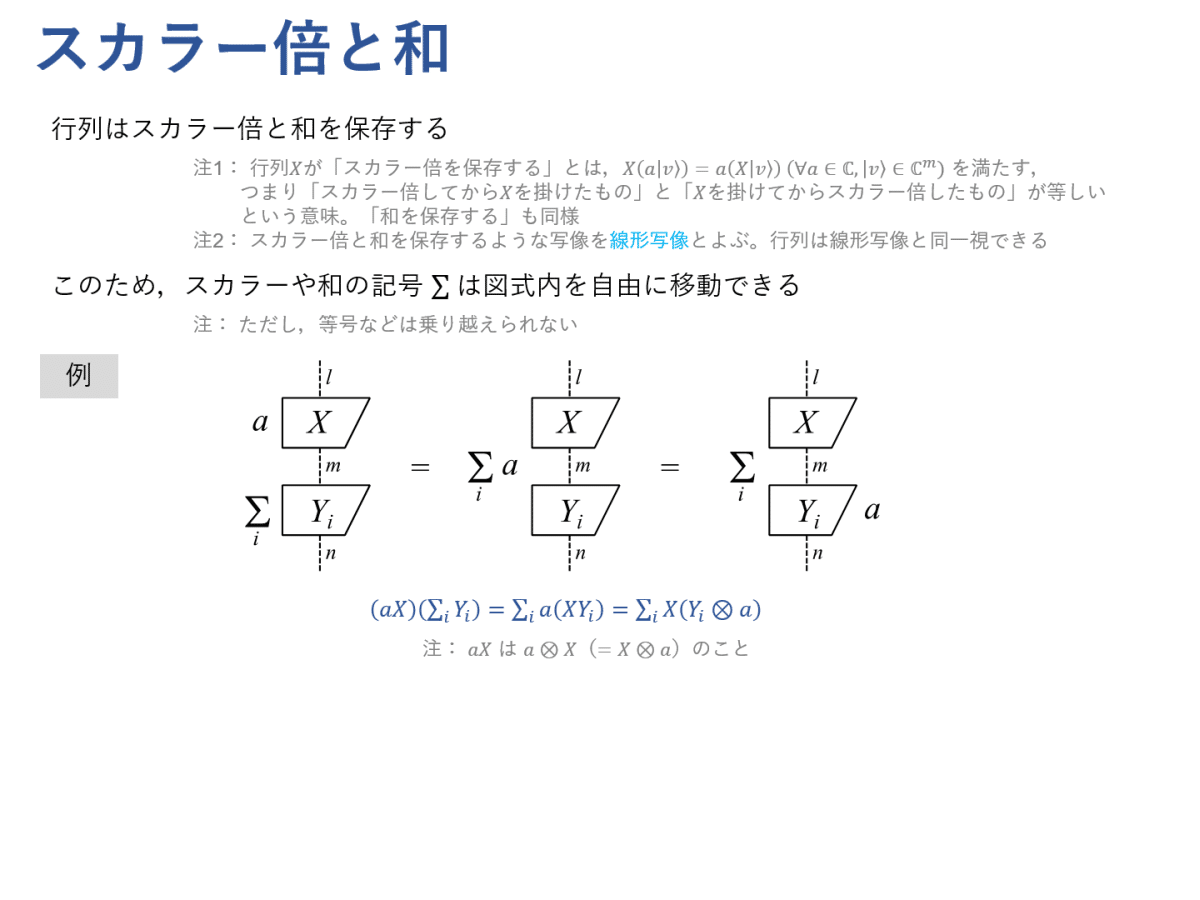
行列は，スカラー倍と和を保存するような写像（線形写像とよびます）とみなせます。ここから，スカラーや和の記号 $${\sum}$$ は図式内を自由に移動できることがわかります。

図式ではブロックを写像とみなして「スカラーや和の記号 $${\sum}$$ が図式内を自由に移動できる」という性質を満たすような写像のみを考えていると解釈できます。このような性質を満たす写像は線形写像（つまり行列）に他なりません。

単位行列は恒等写像（つまり入力をそのまま出力する写像）ですので，単なる破線で描くことにします。この描き方により，単位行列が入力に対して何もしない様子を直観的に表現しています。

逆行列に関する基本的な性質を証明しています。なお，等号の上に付いた (id) のような記号は式番号を表しており，式変形の際に式(id)を用いていることを意味しています。

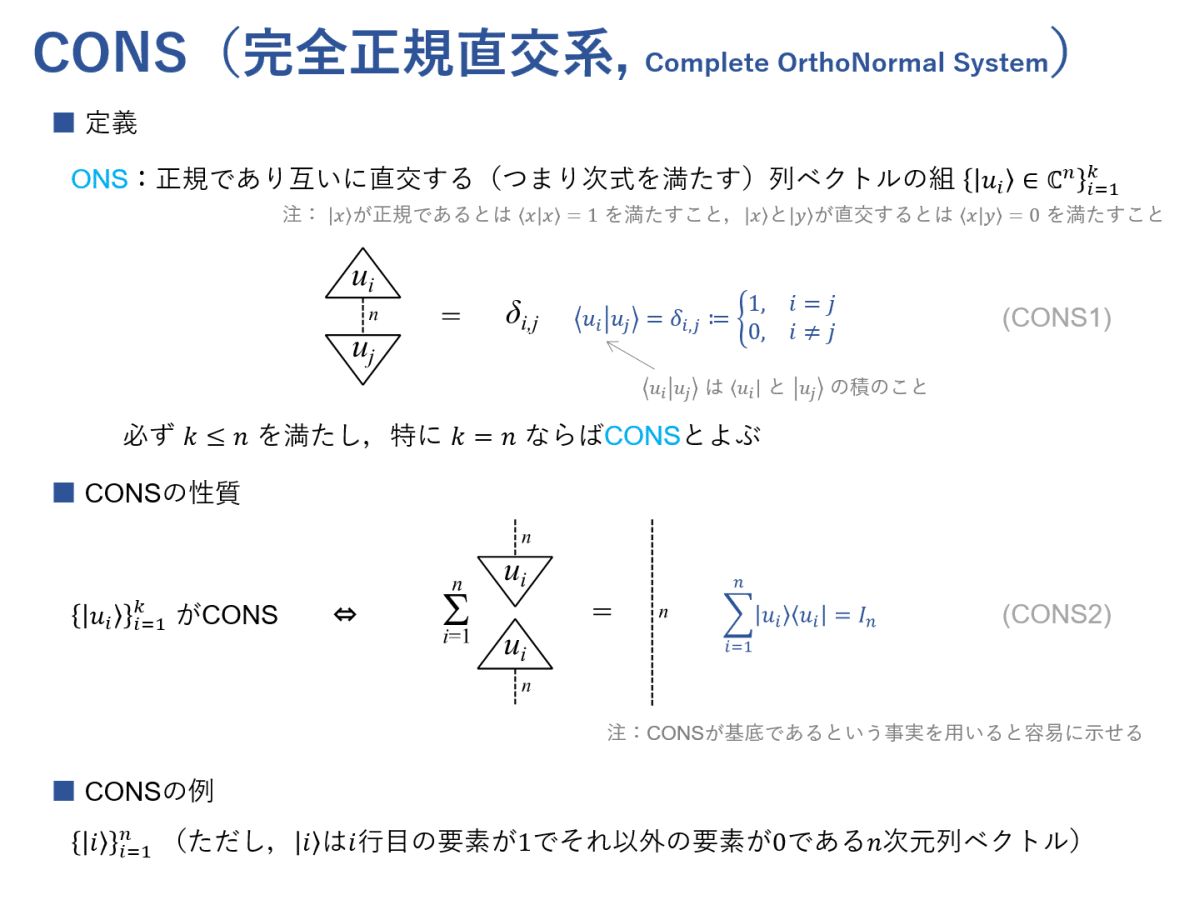
CONS（完全正規直交系）の定義です。CONSは正規直交基底とよぶこともあります。式(CONS1)と式(CONS2)はこれから頻繁に使うことになります。なお，$${n}$$ 次元行ベクトル $${\bra{v}}$$ と $${n}$$ 次元列ベクトル $${\ket{w}}$$ の積を $${\braket{v \vert w}}$$ と表します。$${\braket{v \vert w}}$$ はスカラーです。一方，$${\ket{w}}$$ と $${\bra{v}}$$ の積 $${\ket{w}\bra{v}}$$ は $${n}$$ 次正方行列です。

以下では，$${i}$$ 行目の要素が $${1}$$ でそれ以外の要素が $${0}$$ である列ベクトルを $${\ket{i}}$$ と表します。つまり

$$
\ket{1} =
\begin{bmatrix}
1 \\
0 \\
0 \\
\vdots
\end{bmatrix},
\ket{2} =
\begin{bmatrix}
0 \\
1 \\
0 \\
\vdots
\end{bmatrix},
\dots
$$

です。$${\bra{i}}$$ は $${\ket{i}}$$ の共役転置，つまり $${i}$$ 列目の要素が $${1}$$ でそれ以外の要素が $${0}$$ である行ベクトルです。

二つの空間 $${\Complex^m}$$ と $${\Complex^n}$$ のそれぞれのCONSからテンソル積空間 $${\Complex^m \otimes \Complex^n}$$ のCONSを構成できることを2通りの方法で示しています。なお，$${\Complex^m \otimes \Complex^n}$$ のすべてのCONSがこのように構成できるわけではありません。

CONSの性質を応用すると，コーシー・シュワルツの不等式とよばれる不等式を示せます。

行列の基本的な表現です。このような表記を用いると，次の行列

$$
\begin{bmatrix}
x_{1,1} & x_{1,2} \\
x_{2,1} & x_{2,2}
\end{bmatrix}
$$

は

$$
\sum_{i=1}^2 \sum_{j=1}^2 x_{i,j} \ket{i} \bra{j}
$$

と表せます。列ベクトルはその特別な場合として

$$
\begin{bmatrix}
v_1 \\
v_2
\end{bmatrix}
= \sum_{i=1}^2 v_i \ket{i}
$$

のように表せます。行ベクトルも同様です。

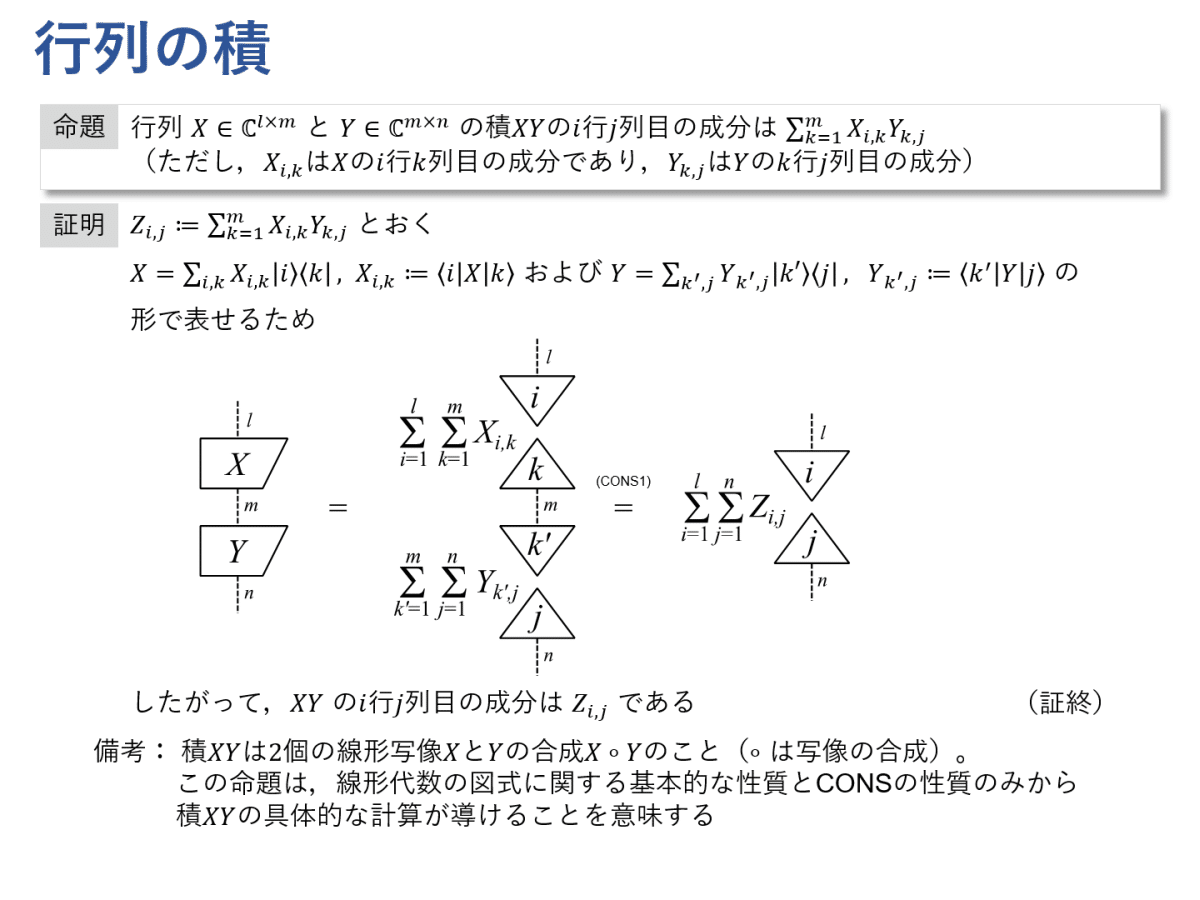
一般には，行列の積 $${XY}$$ は「$${i}$$ 行 $${j}$$ 列目の成分が $${\sum_{k=1}^m X_{i,k}Y_{k,j}}$$ であるような行列」として定義されると思います。ここでは，代わりに写像としての合成 $${X \circ Y}$$ を積 $${XY}$$ と定義することにします。このとき，$${XY}$$ は一般的に定義される積と同じであることを導いています。

---

今回は図式の基礎（行列の積やテンソル積の表現方法など）や線形写像の基礎（CONSなど）を説明しました。次回は，正規行列とスペクトル分解について説明する予定です。