
ロケット打上げと緯度の話
ロケット射場は赤道近くが良いだろうと信じている人は多い。実際にそうなのだろうか?
結論:目的の軌道(目的地)による

ロケット打上げには人工衛星ごとの目的地がある。
宇宙空間では特定の1点に留まることは出来ない。したがって地球周辺であれば地球周回軌道というところで運動し続ける。
射場緯度の有利不利はこの目的の軌道に依存する。
静止軌道と地球低軌道
静止軌道という軌道は赤道直上の高度約3.6万kmにある。日本上空にいれば、ずっと日本上空に見える極めて特殊な軌道。この静止軌道は気象衛星やBS/CS放送衛星に使われている。希少価値のある重要な軌道である。
一方、近年では地球低軌道が多用されている。国際宇宙ステーションがあったり、地球観測、最近の通信衛星、科学衛星、軌道上サービス、宇宙ゴミ掃除と多種多様なミッションの衛星が飛んでいるのは地球低軌道である。地球低軌道は高度2000km以下を指す。地球低軌道は赤道直上だけではなく、軌道傾斜角という赤道からなす角度を持っている。しかも軌道傾斜角は各衛星によって異なる。40度ぐらいのもあれば、90度を超えるものもある。

目的の軌道が地表面から20倍も30倍も離れた場所かつ角度も異なることから、出発地点であるロケット射場の軌道ごとの有利不利も当然異なる。
具体的には、
・静止軌道の場合は赤道近くが有利
・地球低軌道の場合は緯度はほぼ関係ない
となる。
なぜロケット射場は南が良いと思う人が多いか?
これは歴史的な経緯による。
日本では台風災害など防災の目的で気象衛星が早くから望まれていた。そのため、静止軌道に衛星を打ち上げることが大きな目的となっていた。したがって国内で赤道に近い場所(南側)でロケット射場が検討された。また、種子島宇宙センターの開設決定された1966年には沖縄返還がされていなかったのもあり、種子島が選ばれた。
種子島宇宙センターの開設や国産ロケット開発・国産人工衛星開発は多額の費用をかけているために、その理由説明は丁寧に何度も何度も繰り返し行われた。
また、宇宙関係は教育の題材にも使われることから、なぜ鹿児島県にロケット射場が?という疑問に答えるためにロケット=南側良いという単純な説明を教育の場でしてきてしまった。
1970年代からのこの教育を受けた人たちは「ロケット射場は南側良い」という単純化しすぎた理解をしてしまっている。これは現代的な観点からは明らかに勘違いである。

特に時代の要請による部分は理解が難しい。
時代の変化と地球低軌道
現在、人工衛星の多くは地球低軌道に行っている。人工衛星の技術や宇宙利用目的が時代によって変わってきたことによる。
静止軌道の重要性は変わらないが、人工衛星の数という意味では主役は地球低軌道に完全に変わった。
具体的にはどれぐらい?
ロケットの打上場所としての有利不利は増速度(速さの変化量)、専門用語でΔVと言われる数字で比較される。
目的の軌道までに必要なΔVが小さいほど楽に大量の荷物を宇宙に運べる。
射場の緯度と目的の軌道毎の必要ΔVを求めるためのpythonのスクリプトを作った。Githubのgistに貼っているので興味ある人は参考にしてほしい。
https://gist.github.com/ina111/a5cfaecda4720a7ecff971bbf09fcb45
計算方法
詳細な計算はロケットの軌道計算が必要でめんどくさい難しいので、簡単のために地表面から地球の自転分の初速を持ったホーマン遷移軌道で目的の軌道に行くときのΔVを計算する。ホーマン遷移軌道であれば計算式は簡単。
実際には空気抵抗や重力損失、圧力損失と呼ばれるエンジン由来の損失や制御損失と呼ばれる、フラフラ寄り道している速度の損失が発生する。これら速度損失はロケットシステム毎に大きく異るので注意が必要。

この簡易計算のための方法であり、一般的なホーマン遷移軌道計算とは異なる
計算方法の中で、射場の射点(発射場所)の緯度と軌道傾斜角によって計算方法を変えている。
【緯度<軌道傾斜角】の場合には、地表面からのΔV1のときに地球の自転分の初速を勘定している。
【緯度>軌道傾斜角】の場合には、地表面からは真東に打上げをして、軌道上で軌道面変更と呼ばれるマニューバを行う。これは幾何学的に仕方のないことであり、必要ΔVはかなり大きくなる。

計算の中で、損失速度は適当に1.7km/sとしているが根拠はほとんどない。したがって絶対値は気にせずに相対的な大小だけ見てほしい。
計算結果①:緯度と軌道傾斜角による必要ΔVの変化
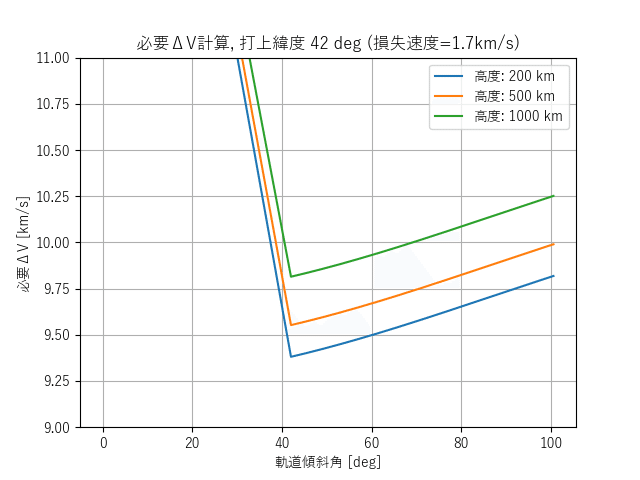
地球低軌道の円軌道に衛星を運ぶために必要なΔVを射場の緯度と軌道傾斜角ごとにプロットしたのが下図。縦軸が下のほうが大量に荷物が輸送できる良い場所・軌道である。
下の線は0.01ぐらいの差で重なってしまって見えにくくなっている。
打上射点緯度の角度よりも高い軌道傾斜角での打上では射点緯度によるΔVの差異はほとんど全く無いことがわかる。
逆に、射点緯度よりも小さい軌道傾斜角に打ち上げようとするとかなり大きなΔVが必要になることもわかる。

計算結果②:高度によるΔVの違い
地球低軌道の中でも高度によるΔVの違いをプロットした。ここでも全体的な数字の違いはそこまで大きくない。高度が500km高くなっても増えるΔVは1~2%程度である。
計算結果③:静止軌道に行く場合の射点の緯度による変化
静止軌道は軌道傾斜角0度である。下図のx軸0degのところを見てほしい。それぞれの射点で射点緯度>軌道傾斜角となり、緯度毎のΔVの違いは極めて大きい。
これは軌道上に上がったあとで軌道面変更をしているからである。前述の2例ではΔVの違いは1未満など小さかったが静止軌道では緯度が大きく効いてくる。
また、ΔVはロケットの大きさに指数関数的に効く。もしくはペイロード重量に大きく作用する。これだけ必要ΔVが違うと射場の緯度は大変重要になる。
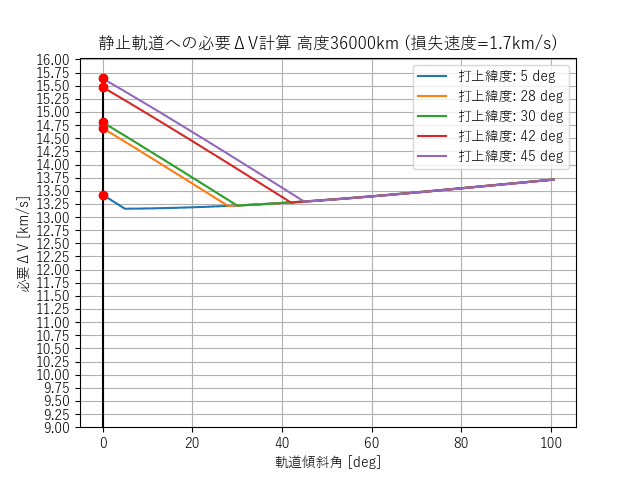
北緯28度はアメリカのケネディ宇宙センター
北緯30度は日本の種子島宇宙センター
北緯42度は北海道スペースポート
北緯45度はカザフスタンのバイコヌール宇宙基地
とかなり大雑把な数字で再現しているつもり
その他①:スーパーシンクロナス・トランスファー軌道
静止軌道に行く場合は、緯度の違いの影響を減らすためスーパーシンクロナス・トランスファー軌道という軌道で打上げることがある。地球から一旦大きく離れるような苦労をしてでもΔVを下げるのである。

最大で静止軌道の2倍の高度の遠地点まで行っている
その他②:地球低軌道でも軌道傾斜角0度の例もある
地球低軌道でも極めて珍しく軌道傾斜角0度付近に飛ばした衛星があった。地球低軌道での低い軌道傾斜角の衛星はほとんど見たことがなかったので印象深い。NASAとイタリア宇宙機関のImaging X-ray Polarimetry Explorer(通称:IXPE)と呼ばれるX線天文衛星である。
特殊な軌道だったので、元々はペガサスロケットという飛行機でロケットを途中まで運ぶ方式で打上げ予定であったが、SpaceX社のFalcon9ロケットに変更された。
ペガサスロケットの場合は飛行機で赤道付近まで運んでから打ち上げるので良かったが、Falcon9はケープカナベラル(ケネディ宇宙センター、北緯約28度)からの打上げであった。緯度>軌道傾斜角であり、軌道面変更による必要ΔVが大きくなる。
そのため、大型ロケットであるFalcon9のフェアリングサイズに似合わない小型の衛星が搭載されるという珍しい光景となった。


その他③:計算詳細
プログラムの詳細を知りたいという声があったので記事に貼っておく。清書するのは面倒だったので手書き。ここまでの詳細な計算は大学生以上向き。

この記事が気に入ったらサポートをしてみませんか?
