
検査に「誤り」が出てしまう根本的な理由を、グラフを見ながら考えてみる
病気かそうでないかを調べる、「検査」。
検査では、ときどき「誤った結果」が出る。
本当は病気なのに「病気ではない」という結果が出たり、
健康なのに「病気です」という結果が出たり・・・
なぜ検査には、「誤り」が出るんだろう?
僕は医師ではないし、
数学の「確率」や「統計」は苦手だ。
この話は、ほんとは確率や統計の言葉で説明する必要がある。
でも今回は、なるべく見た目だけで分かる感じで、説明してみたい。
「バラツキ」と 正規分布
バラツキのないモノゴトなんて、世の中には存在しない。
同じ種の生物でも、
体長 や 体重 はバラつくし、
同じ工業製品でも、
大きさ や 重さ はバラつくし、
天体観測で同じ星の運行を調べても、
その観測データはバラつく。
例えば、魚の「体長」を考えてみる。
テレビとかで、魚の美しい大群を眺めてると、
全く同じ大きさの魚が、
大量に群れてるような感じがしてくるけど・・・
一匹ずつ丁寧に体長を測ってみると、どうだろう?
例えば、赤い魚の群れがあって、

一匹ずつ体長を測ってみる。
たくさんの魚の体長を測って、グラフにすると・・・
大抵の場合、こういう、美しいグラフになる。

このグラフのかたちを
「正規分布」
って言ったりする。
正規分布のかたちは、
真ん中が高くて、
両端に行くほど低くて、
そして、左右対称。
体長の平均を 30 cm とすると・・・

体長が 29 cm とか 31 cm とか、
30 cm に近い魚は、たくさんいる。

だからグラフは、真ん中が高い。
体長が 30 cm とはかなり違う魚、
例えば 25 cm とか、35 cm とか、
そんな魚は、さすがに少ないし、

20 cm とか、40 cm とか、
そんな魚は、さらにもっと少ない。

だからグラフは、両端に行くほど低くなる。
そしてなぜか、多くの場合、
平均より 5 cm 大きい魚と、
平均より 5 cm 小さい魚は、
だいたい同じ数になる。
だからグラフは、左右対称になる。
そして、このグラフのかたちを、
数式で表すと、こうなるらしい・・・

生物の体長のバラツキも、
工業製品の大きさのバラツキも、
星の運行の観測データのバラツキも、
なぜか、多くの場合は、正規分布に従う。
ニュートンの運動方程式に従って、砲弾が飛んで行く、
とかなら、まだ分かるけど・・・
バラツキが数式に従うって、どゆこと?
不思議すぎて、ぜんぜん意味が分からない。
でも実際に、
多くの モノゴト の バラツキ は、
正規分布 に従うんだ。
二種類の魚を「体長」で見分ける
ある人が、
病気か、病気でないか?
を検査で判定する、っていうと、
なんか専門的で、難しい感じがする。
でも、
「二種類の魚を見分ける」
っていう話なら、どう?

ただし、
検査を1種類しかやらないなら、
それは、
たったひとつの指標を手がかりに、
「これは、どっちの種類の魚か?」
を判定する、
ということに等しい。
例えば、魚の「体長」しか手がかりがない、とする。
分かるのは「体長」だけ。
魚を見ることはできないから、色も分からない。
「体重」も分からない。
ただ体長の値だけが、ずらっと並んでる、と思ってほしい。
赤い魚の体長は、平均 30 cm、
緑の魚の体長は、平均 20 cm、
とする。
赤い魚も、緑の魚も、体長にバラツキがあるから、
グラフにすると、こんな感じ。

ここで、体長 30 cm の魚は、
赤い魚 だろうか?
緑の魚 だろうか?
グラフを見てみると・・・
体長 30 cm なら
「たぶん赤い魚」
だと言ってほぼ間違いないだろう。

体長が 30 cm もある緑の魚は、そんなにたくさんはいないから。
では、体長 20 cm の魚は?
体長 20 cm なら
「たぶん緑の魚」
だと言って、ほぼ間違いない。

体長 20 cm の赤い魚は、そんなにたくさんはいないから。
というわけで、
「体長 30 cm 以上の魚は、赤い魚だ」
と判断しちゃえばいいだろうか?
いやいや、そうすると、
「体長 30 cm 未満の魚は、みんな緑の魚」
なわけ?
「体長 30 cm 未満の赤い魚」も
こんなにいるっていうのに!

じゃあ、
「体長 20 cm 未満なら、緑の魚だ」
っていう基準にする?
いやいや、
「体長 20 cm 以上の緑の魚」
も、こんなにいますけど?

というわけで、真ん中あたりをとって、
「体長 25 cm 以上の魚は、赤い魚」
「体長 25 cm 未満の魚は、緑の魚」
ぐらいに、してみようか・・・?

バランス的には、ここらへんがよさそうだ。
誤った判定結果
でも、このグラフを見てみると・・・
「体長 25 cm 以上の緑の魚」が、
こんなにいる・・・

この魚たちは、
「赤い魚」だと判定されたけど、
実は「緑の魚」だ、
っていう魚たち。
「体長 25 cm 未満の赤い魚」も、
こんなにいる・・・
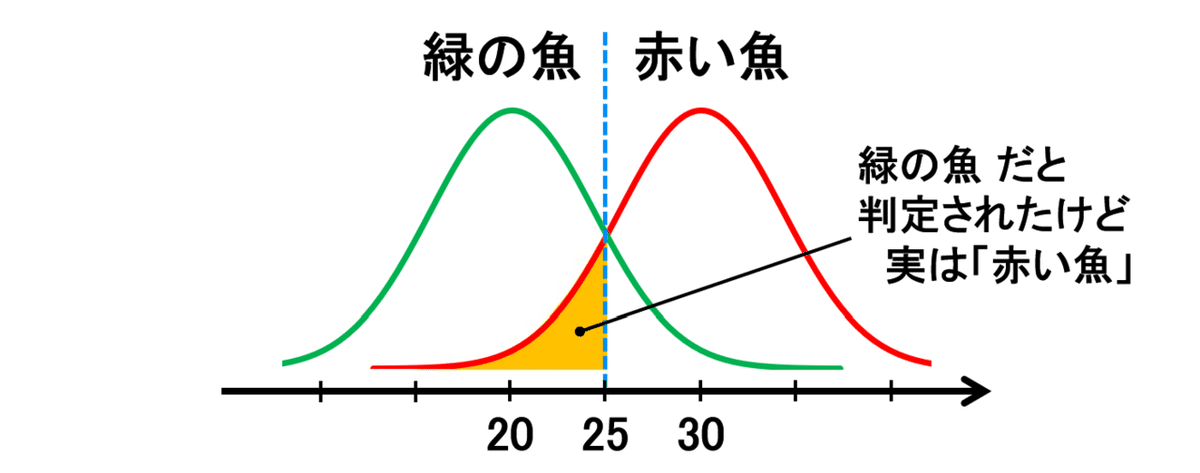
この魚たちは、
「緑の魚」だと判定されたけど、
実は「赤い魚」だ、
っていう魚たち。
こういうふうに、
「誤った判定結果」
は、必ず出てしまう。
病気の検査も、同じだ。
検査で測る値に、バラツキがある限り、
このような「誤り」は必ず出てしまう。
そして、
世の中のあらゆるモノゴトには、
バラツキがある。
検査における誤った判定結果
ある病気を判定するための検査方法があって、
その方法で検査すると、
健康な人は、値が低く
病気の人は、値が高く
なるとする。
でも、この検査の値にも、バラツキがある。
「実は健康な人」の検査の値も、
「本当に病気の人」の検査の値も、
バラつくから・・・
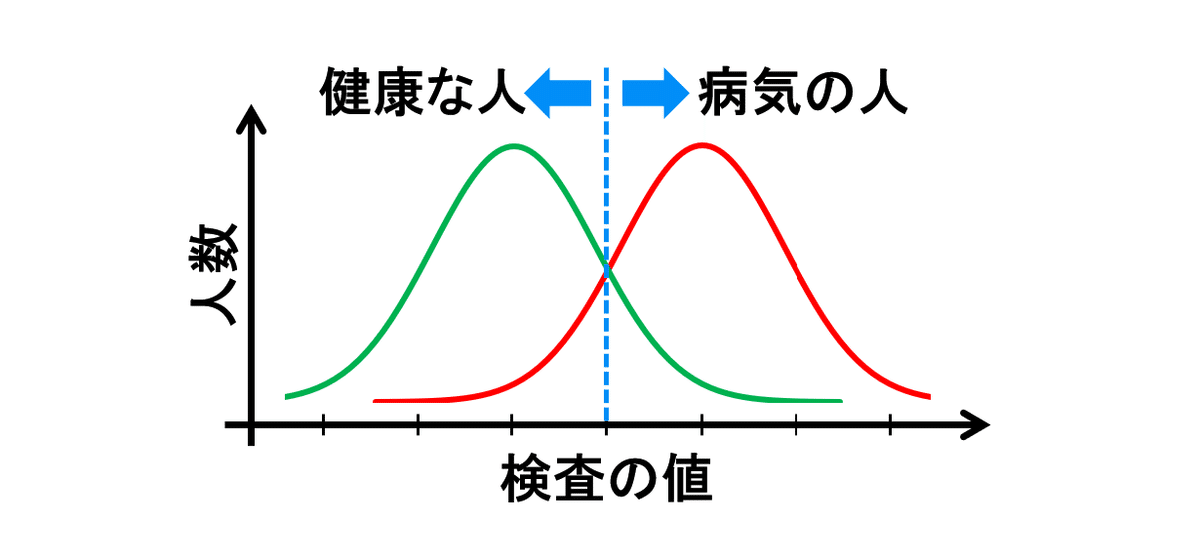
グラフにしてみると、こんな感じ。

このふたつの山が、離れていたら苦労しないけど・・・

現実には、多くの場合は、こんな感じで少し重なってしまう。

そして、このグラフのどこかに、
「健康な人 と 病気の人 との境界線」
を引く必要がある。
例えば、このへんに、境界線を引くと・・・

このぐらいは、
病気だと判定されたけど、「実は健康な人」
が出てしまう。

そして、このぐらいは、
病気ではないと判定されえたけど、「本当は病気の人」
が出てしまう。

どうだろう?
こうしてグラフを眺めると、
「誤った判定結果」は
どうしても出てしまう
と分かると思う。
ミスのない「完璧な検査」というものは、
世の中に存在しないんだ。
「なんとなく不安」で、検査を受けてしまうと
ところで、このグラフは
「実は健康な人」も、
「本当に病気の人」も、
同じぐらいの高さの山として、描いている。
つまり、
「実は健康な人」と、「本当に病気の人」 の人数が同じぐらい
というグラフになっている。
でも、実際には検査を受ける人たちって、
なんか熱っぽい、とか、
なんか気分が悪い、とか、
そういう理由で病院に来た人たちがほとんどだろう。
そういう人たちには、
「実は健康な人」は、あまりいないだろう。
「本当に病気の人」が、多いはず。
だから、実際に検査を受けた人たちのグラフって、
たぶんこんな感じになる。

つまり、実際には、
病気だと判定されたけど、「実は健康な人」
は、普通はそんなに出ないはずだ。
ところが、
「なんか不安だから、念のため検査を受けたい。」
という人が増えたら、どうだろう?
検査を受ける人の中で、
「実は健康な人」
の人数が増えて・・・
こんなグラフになってしまう。

つまり、
病気だと判定されたけど、「実は健康な人」
が、増えてしまう。
感染症によっては、強制的に入院させられたりもするようなので、
病気だと判定されたけど、「実は健康な人」
が増えると、病院のリソースを圧迫する、
・・・というわけだ。
(※ とはいえ、感染すると重症化するリスクが高い人たち(高齢の人たち、など)もいるので、一律に「検査をなるべく受けるな」と言いたいわけじゃない。)
「あり / なし」の二択の検査
ここまで読んでくれた人の中には、
「これって、検査結果の値にバラツキがある場合でしょ?」
「ウイルス検査は、違うでしょ?」
と思う人もいるかも知れない。
もっともな疑問だ。
ウイルス検査は、
ウイルスあり(陽性)か、
ウイルスなし(陰性)か、
の二択だ。
「あり」の結果とか、「なし」の結果は、
バラツキようがない。
でも、こういう検査でも、
実は検査装置の中ではいろんな値が出ていて、
装置の中で、境界線を引いていたりする。
つまり、「あり / なし」の検査でも、
元になる値には、バラツキがあることが多いので、
今回書いたようなことが、基本的には当てはまると思う。
(まとめ)
正規分布をイメージする
ここまで長々と書いたことを、
完璧な検査なんてないんだから、
そりゃ、検査にも見落としは出るよね。
と言ってしまえば、それまでだろう。
でも、こういうふうに、
正規分布
をイメージしながら、
・見落としは、なぜ発生してしまうのか?
・見落としは、検査を行った人のミスなのか?
(ミスの可能性も否定はできないが)
・見落としは、検査装置の故障なのか?
(故障の可能性も否定はできないが)
を、考えてみると・・・
世間で起きていることが、少し違って見える
・・・と、思うんだけど
どうだろうか?
(補足)
■ 偽陽性 と 偽陰性
用語の説明は、あまり好きじゃないけど・・・
「病気です」という検査結果を
陽性
「病気じゃありません」という検査結果を
陰性
という。
そして、
病気だと判定されたけど、「実は健康な人」
は、「偽(にせ)の陽性」といいうことで、
偽陽性(ぎようせい)
という。
逆に、
病気ではないと判定されえたけど、「本当は病気の人」
は、
偽陰性(ぎいんせい)
という。
偽陰性が出ると、
「本当は病気の人」を見落としたってことで、
「検査に見落としがあった」と報道されることもある。
■ 正規分布以外の要因
ここまで書いておいてなんだけど、
偽陽性 や 偽陰性 の原因は、バラツキだけじゃない。
だって、考えてみて欲しい。
病気の疑いがある人の体から採取されたサンプルが、
検査する場所にたくさん送られてくるんだ。
サンプルがびっしり並んでいて、
陽性のサンプルの、目に見えないほど小さな1滴が、
ちょっとしたはずみで、隣の陰性のサンプルに
飛び込んでしまうかも知れない。
そうなったら、その陰性サンプルは偽陽性になってしまう。
サンプルを採取する人が、採取に慣れていないと、
うまく取れてないサンプルが送られてくるかも知れない。
すると、病気にかかった人から取ったサンプルなのに、
検査結果が陰性になるかも知れない。
つまり、偽陰性の発生だ。
もちろん、こういうことが起きないように、
いろんな工夫がされているはずだ。
でももし起こってしまうと、
正規分布のお話とは全く違うレベルで、
検査結果に影響するだろう。
この記事が気に入ったらサポートをしてみませんか?
