【ABC351】AtCoder ABC351 Problem Eを解き直す

2024年4月30日 17:47

AtCoder Beginner Contest 351、参加して来ました。

ABCと３問AC。なんとなく、D問題は手が届きそうになく、E問題ならワンチャンあるかな、と思った所、予想通りTLE。悔しいので、2日経って改めて解き直しました。その経過をこちらに記載して行きたいと思います。言語はPython (PyPy 3.10-v7.3.12)を利用しています。

AtCoder ABC351 problem E

問題内容は以下からご確認下さい。

問題内容の概要

xy平面上に配置された２点間をナナメ移動で到達する事を考えます。
ナナメ移動というのは、こんなイメージを指します。

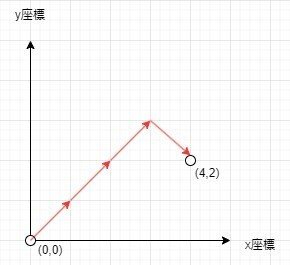
もし到達出来るならその移動回数をdist($${P_1}$$,$${P_2}$$)とします。上図のケースなら4になります。到達出来ない場合もあるので、その場合はdist($${P_1}$$,$${P_2}$$)=0とします。

今回の問題の場合、$${xy}$$平面上に複数個の点が存在します。この時発生する、全てのdist($${P_i}$$,$${P_j}$$)の総和を求めるのが今回の目的となります。

提出１回目（コンテスト内）

まずは、提出したコードを記載します。一応、コメントは後から付け足したものです。

def function():
    # 標準入力
    n = int(input())
    a1 = []
    a2 = []

    # x+yの2で割った余りが異なる点同士は到達不可能なので、
    # それらを先に組み分けしておく
    for _ in range(n):
        a = list(map(int,input().split()))
        if((a[0]+a[1])%2 == 0):
            a1.append(a)
        else:
            a2.append(a)

    # 計算関数の定義
    def sumup(a):
        num = 0
        if(len(a)==0):
            return 0
        for i in range(len(a)-1):
            for j in range(i+1,len(a)):
                if(abs(a[i][0]-a[j][0]) > abs(a[i][1]-a[j][1])):
                    num += abs(a[i][0]-a[j][0])
                else:
                    num += abs(a[i][1]-a[j][1])
        return num
    
    print(sumup(a1)+sumup(a2))
    return

if __name__ == "__main__":
    function()

コンテスト内プログラムでの考察

今回の問題では、２点間で到達が不可能な組み合わせが存在しています。例えば、(0,0)と(1,2)の２点間は到達が不可能です。原点からナナメ移動を考えた時、右上に飛ぶ時は(0,0)→(1,1)となります。どの向きにジャンプする場合でも、必ず$${x}$$と$${y}$$座標がそれぞれ±1するので、原点から(1,2)には到達出来ません。
これらは各点の$${x,y}$$座標の和が、奇数か偶数かで分ける事が可能です。$${xy}$$座標の和が奇数である点同士は到達可能だし、偶数である点同士も同様です。一方で、$${x,y}$$座標の和が奇数の点と、偶数の点の間では到達が不可能です。
この判断を都度行うと計算コストになるので、最初にグループ分けしておく事で、計算量が減らせるでしょう。
しかしながら、それ以降の部分は素直に計算しました。2点をナナメで移動した時の最短距離は、2点間のx軸の差とy軸の差の大きい方になります。それを都度加えました。
予想通り、本プログラムはTLE(時間切れ）となりました。iとjをループしている箇所の計算量が大き過ぎるので、ここを工夫する必要があるのですが、その解法が導き出せず、時間切れとなりました。ここから、解いていきます。

公式の解説

公式より解説が出ております。面倒な方はこちらからご覧下さい。しかし、恥ずかしながら、私はこれを読んだだけではサッパリ分かりませんでした。

なので、ここから解説を読んだ上で自分でまとめていきます。

戦略

この問題は、複数個発生する２点間の距離の計算を、いかにまとめて計算出来るかが肝になります。
求めるdist($${P_i}$$,$${P_j}$$)の個数は、最大で$${N*(N-1)/2}$$個になるので、制約により最大で$${10^{10}}$$程度の計算量が発生します。これは時間内に収めるのは不可能なオーダーです。
しかしながら、dist($${P_i}$$,$${P_j}$$)を計算する上で、現状の計算方法（差の大きい方を選ぶ）だと$${x}$$軸と$${y}$$軸の値を比較して評価する必要があり、このままではまとめて計算する、という方針を立てるのに互いの数値の相互関係が邪魔になります。なので計算上、$${x}$$と$${y}$$の値を分割出来るとより計算し易くなりそうだ、という事が言えると思います。

マンハッタン距離の適用

マンハッタン距離とは、２点間を座標の軸に沿って移動した時の最短距離の事です。以下の図の様なイメージです。今回の移動経路はまさにこのパターンであり、これを利用して計算する事が可能です。

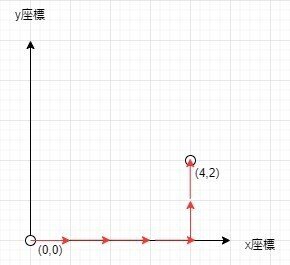
点$${P}$$のx,y座標を($${x_i}$$,$${y_i}$$)とした時、$${P_i}$$,$${P_j}$$間のマンハッタン距離$${d}$$は、$${d =|x_i-x_j| + |y_i-y_j|}$$となります。この時、$${x}$$と$${y}$$は疎結合なので、分離する事が可能です。
実際に複数のマンハッタン距離の和を考えた時、$${d_1 + d_2 = (d_{x_{d1}} + d_{x_{d2}}) + (d_{y_{d1}} + d_{y_{d2}})}$$の様に、$${x}$$と$${y}$$を個別に計算して求める事が可能になります。これが後で効いてきます。

xy座標軸の回転

今回移動する方向はナナメなので、マンハッタン距離を計算する軸はxy平面上ではあるものの、45°傾いた軸に沿って移動する事になります。この為、各点はこの傾いた軸に合わせて、新座標軸での表現に変更する必要があります。上記より、まずはxy座標軸を45°回転させます。
座標計算をするにあたり、三角関数を利用します。分かり辛いので、まず既存のxy軸で表現します。

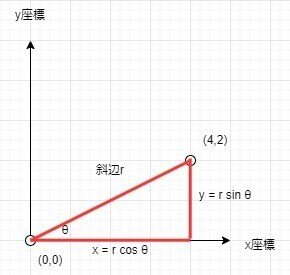
点Pの座標は、斜辺ｒの値を用いた場合、x,yは以下の様に表現できます。

$$
(x,y) = (r \cos \theta,r \sin \theta)
$$

続いて、ナナメ移動の方向に沿った軸を新XY軸として導入します。この軸はxy軸から見て45°傾いている状態です。

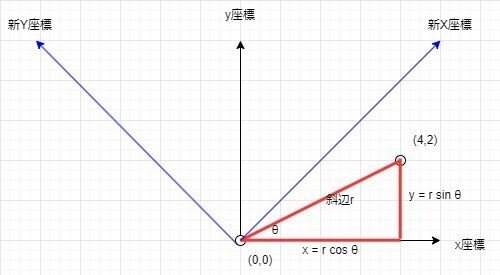
従来の座標から、新座標軸に変換しようと考えた時、座標軸は45°ずれています。また、新座標軸はナナメ１回分が１目盛りに相当すると考えると計算が楽なので、$${\sqrt2}$$倍のスケールと考えます。
この為、新座標軸に表現を変換する場合、全体に-45°回転させた上で、$${1/\sqrt2}$$倍すると、適切な表現になりそうです。

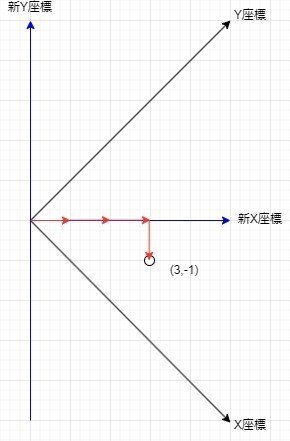
なので点Pの座標軸を新座標軸に変換した場合、以下の式になります。

$$
(X,Y) = (\frac {r \cos(\theta-45^{\circ})} {\sqrt2} ,\frac {r \sin (\theta-45^{\circ})} {\sqrt2})
$$

これは正弦・余弦の加法定理を使う事で、もう少し分かり易い記法に変換する事が可能です。以下を利用します。

$$
\cos(\alpha - \beta) = \cos\alpha*\cos\beta + \sin\alpha*\sin\beta \\
\sin(\alpha - \beta) = \sin\alpha*\cos\beta - \cos\alpha*\sin\beta
$$

ここで$${\beta}$$は45°になるので、もう少し分かり易い記法が出来ます。

$$
\cos(\alpha - 45^{\circ}) = \cos\alpha*\cos 45^{\circ} + \sin\alpha*\sin 45^{\circ} \\
= \frac {\cos\alpha + \sin\alpha} {\sqrt2} \\
\sin(\alpha - 45^{\circ}) = \sin\alpha*\cos 45^{\circ} - \cos\alpha*\sin 45^{\circ} \\
= \frac {\sin\alpha - \cos\alpha} {\sqrt2} \\
$$

これを利用して、既存の点P座標を新座標軸系に変換すると、以下の様になります。

$$
(X,Y) = (\frac {r \cos(\theta-45^{\circ})} {\sqrt2} ,\frac {r \sin (\theta-45^{\circ})} {\sqrt2}) \\
= (\frac {r(\cos\theta + \sin\theta)} {2} , \frac {r(\sin\theta - \cos\theta)} {2})
$$

さらにこれらは元の座標軸での表現に戻すことが出来ます。以下の様になります。

$$
(X,Y) = (\frac {r(\cos\theta + \sin\theta)} {2} , \frac {r(\sin\theta - \cos\theta)} {2}) \\
= (\frac {x+y} 2, \frac {y-x} 2)
$$

これより、45°傾いた新座標系で考え直す場合、x+yとy-xをそれぞれ用意しておけば簡単に再表現出来る事が分かりました。xとyは点毎に与えられている数値であり、これらの和や差の値も機械的に簡単に算出する事が可能です。

新座標におけるdiffのまとめ計算

ここまでで、新座標系でのマンハッタン距離の計算の準備が整いました。ここから複数点のマンハッタン距離の総和を求める部分に入って行きます。

まずは少ない点の数で考慮してみます。点を３つ用意して、試しにそれらの点間で総和を求めて行きます。

このケースで考える必要がある組み合わせは、$${(P_1,P_2),(P_1,P_3),(P_2,P_3)}$$の３つです。これらのマンハッタン距離を導出して総和を求めます。

$$
d_{12} = | X_1 - X_2 | + | Y_1 - Y_2 | = | 1-6 | + | 1-2 | = 6 \\
d_{13} = | X_1 - X_3 | + | Y_1 - Y_3 | = | 1-3 | + | 1-5 | = 6 \\
d_{23} = | X_2 - X_3 | + | Y_2 - Y_3 | = | 6-3 | + | 2-5 | = 6 \\
\\
\displaystyle\sum_{i=1}^{2}\displaystyle\sum_{j=i+1}^3 \text{dist}(P_i,P_j) = d_{12} + d_{13} + d_{23} = 18
$$

これより、この問題において、マンハッタン距離の総和は18でした。
これは答えとして持っておきます。

しかしながら、絶対値計算が邪魔なので、各X座標とY座標をそれぞれ配列化し、昇順ソートさせます。ここでXとYは計算において疎結合なので、それぞれの添字が変わっても計算結果に影響はありません。
ソートをする事により大小関係が明確になったので、絶対値を考慮する必要が無くなります。そして以下が立式出来ます。

$$
X[ ] = [X_1,X_3,X_2] = [1,3,6] \\
Y[ ] = [Y_1,Y_2,Y_3] = [1,2,5] \\
\\
\displaystyle\sum_{i=1}^{2}\displaystyle\sum_{j=i+1}^3 \text{dist}(P_i,P_j) = d_{12} + d_{13} + d_{23} \\
= |X_2-X_1| + |X_3-X_1| + |X_3-X_2| + |Y_2-Y_1| + |Y_3-Y_1| + |Y_3-Y_2| \\
= (X_2-X_1) + (X_3-X_1) + (X_3-X_2) + (Y_2-Y_1) + (Y_3-Y_1) + (Y_3-Y_2)
$$

こうすると、気付くのはいくつかのXやYを打ち消す事が出来る事に気付きます。打ち消した後の結果は、以下になります。

$$
\displaystyle\sum_{i=1}^{2}\displaystyle\sum_{j=i+1}^3 \text{dist}(P_i,P_j) = d_{12} + d_{13} + d_{23} \\
= (X_2-X_1) + (X_3-X_1) + (Y_3-Y_2) + (Y_2-Y_1) + (Y_3-Y_1) + (Y_3-Y_2) \\
= (2X_3 -2X_1) + (2Y_3 -2Y_1)
= (2*6 - 2*1) + (2*5 - 2*1) = 18
$$

結果も、先に１個ずつ求めた値と等しい値になっている事が分かります。

この様に、それぞれの点間の距離を都度計算しなくても、求められそうな感じがします。試しに点を４点に増やしてみます。

$$
\displaystyle\sum_{i=1}^{3}\displaystyle\sum_{j=i+1}^4 \text{dist}(P_i,P_j) = d_{12} + d_{13} + d_{14} + d_{23} + d_{24} + d_{34} \\
= (X_2-X_1) + (X_3-X_1) + (X_4-X_1) + (X_3-X_2) + (X_4-X_2) + (X_4-X_3) \\ +(Y_2-Y_1) + (Y_3-Y_1) + (Y_4-Y_1) + (Y_3-Y_2) + (Y_4-Y_2) + (Y_4-Y_3) \\
= (3X_4 + X_3 - X_2 - 3X_1) + (3Y_4 + Y_3 - Y_2 - 3Y_1)
$$

同じような形で立式出来る事が分かります。打ち消しを考慮すると、最終的に以下の形式に変更する事が可能です。

$$
\displaystyle\sum_{i=1}^{N-1}\displaystyle\sum_{j=i+1}^N \text{dist}(P_i,P_j) =
\displaystyle\sum_{i=1}^{N}(2i-1-|X|)X_i + \displaystyle\sum_{i=1}^{N}(2i-1-|Y|)Y_i
$$

$${X_i}$$と$${Y_i}$$はそれぞれ、$${\frac {x+y} 2}$$と$${\frac{y-x} 2}$$で求められることが分かっているので、これで全ての計算式と情報が揃いました。

提出２回目

以上をふまえた上で、以下のコードで提出しました。

def function():
    # 標準入力
    n = int(input())
    a1 = []
    a2 = []

    # x+yの2で割った余りが異なる点同士は到達不可能なので、
    # それらを先に組み分けしておく
    for _ in range(n):
        a = list(map(int,input().split()))
        if((a[0]+a[1])%2 == 0):
            a1.append(a)
        else:
            a2.append(a)

    # 計算関数の定義
    def sumup(a):
        X = []
        Y = []
        num = 0
        for c in range(len(a)):
            X.append(a[c][0]+a[c][1])
            Y.append(a[c][1]-a[c][0])
        X.sort()
        Y.sort()
        XY_len = len(X)
        for i in range(XY_len):
            num += (2*i + 1 - XY_len) * (X[i] + Y[i]) // 2
        return num

    # 結果の出力
    print(sumup(a1) + sumup(a2))
    return

if __name__ == "__main__":
    function()

ほぼ、上の項で説明したものをプログラムに落とし込んだだけです。pythonは添字が0から始まるので、そこの部分で多少式が異なっていたり、$${X}$$と$${Y}$$の配列の長さは同じになるので、そこを共通の値として利用していたりしますが、大筋は変わりません。

これを提出して、ようやくACとなりました。

計算量の見積もり

最後に、計算量を見積もっておきます。
これは解説にも述べられている通りですが、グループ分けした二つのグループのX,Y座標配列について、それぞれ昇順ソートをかけています。これの計算量は$${O(N \log N)}$$になります。しかしながら、その後の計算は$${O(N)}$$となります。これは十分に高速です！

おわりに

正直、自力で制限時間内に解けるかと言われると、かなり難しいと言えますね。かなり数学的な知識が必要でした。一定の慣れと経験が必要そうな問題だったと言えます。どちらかと言うと、高速化の技術というよりは、「高速化する為にどうするか」に強く焦点が当たっていた問題と言えるのかもしれません。
しかしながら、解説を読んだ上ではあるものの、内容を適切に紐解いた事で、自分の理解には繋がりました。次は解いてやるぞ。

この記事が気に入ったらサポートをしてみませんか？