ハフマン符号化(準備)

これから考える問題は、ある情報源が発する記号を、0と1で二値符号化する場合、もっとも最適な符号化方法は存在するのか、するとしたら具体的にどう構築するかです。さらに情報源は各記号をある確率に従って独立に発信していると仮定します。

ここで重要なルールとして、符号化の長さは一定でなくてもいいとします。例えばa, b, cをある確率で発する情報源があったとき、aを0で、bを1で、cを01で符号化することが考えられます。このときa, bの符号長は１、cは２となります。

復号可能性

また符号は復号できないといけない。例えば上の例で、符号列が010だったとき、これは元のメッセージがabaかもしれないし、caかもしれません。このように復号の仕方が一意に定まらない符号は除いて考えます。復号できる符号を復号可能と呼ぶことにします。

最適な符号

また、最適化という観点から符号を眺めたとき、最初に思い浮かぶのは平均符号長がどれくらい短いかです。平均符号長<d>とは、記号a1, a2, …, aKを確率p1, p2, …, pKで発する情報源があり、それを復号可能な符号で符号化したときの符号長がそれぞれd1, d2, …, dKだったとして、

で定義されます。これを最小にするような符号化が見つかれば、それが最適であるとします。最適な符号は長さあたりのメッセージ送信コストがもっとも小さいといえます。(いまは各符号を送信するのにかかるコストは同じだとしています。)もしメッセージ長が十分大きいときは、そこにpkの割合だけ記号akが含まれることがほぼ確実になります。このとき平均符号長は記号あたりの符号長と一致することが確認できます。

Kraft-McMillan不等式

ハフマン符号化に入る準備として、まず復号可能な符号の満たすべき条件を考えます。この条件のおかげで、考えるべき符号の集合がずっと小さくなるのです。結論からいうと、復号可能な符号は

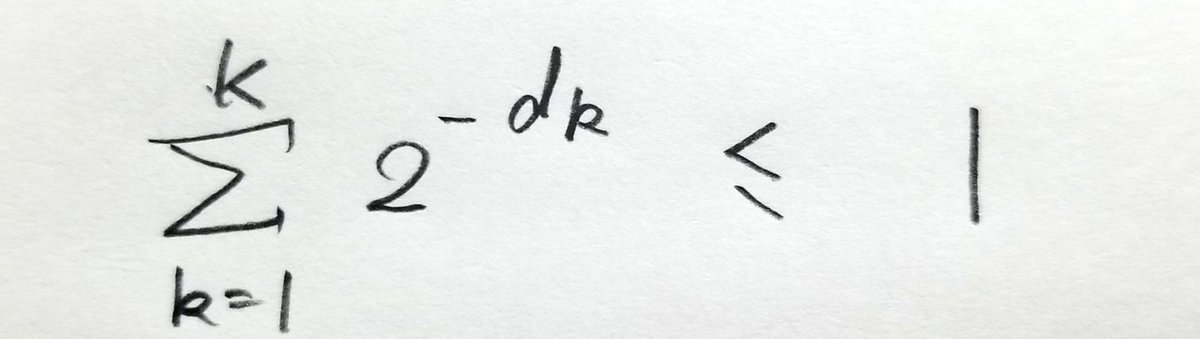
を満たす必要があります。この証明の本質は次の事実に着眼することにあります。すなわち長さがLの異なる符号列(メッセージの長さではなく、それを符号化した符号の列の長さがLであることに注意)の総数N(L)が2^Lを超えないということです。なぜなら2^Lという数は二値符号化で表せる長さLの符号列の数の上限だからです。

さて証明に入ります。まずN(L)の満たすべき等式を導きます。長さLの符号列をその最後の符号で場合分けすると、K通りあることはもちろんです。なので長さdの符号の数をn(d)とすれば

がL>dmaxについて成り立っている必要がある。ここでdmaxはdkのうち最大のものです。ここでN(0)=1とおき、さらにL<0に対しN(L)=0と定義すれば、任意のL>0について上の等式が成立するようにできます。

実際例えばL=1とすると、右辺はn(1)に等しく左辺はN(1)なので辻褄があいます。L=2であればN(2)=n(1)^2+n(2)が出てきてこれも正しい。これを繰り返せば任意のN(L)が求まるわけです。

このように整数のインデックスがついた量(ここではN)があって、異なるインデックスの間で関係式が成り立つとき、母関数を考えるのが有効です。母関数とは級数の係数に注目量を持ってきたもので、以下で定義されます。

ここで実数xの動ける範囲(級数の収束する範囲)はあとで考えます。N(L)の満たすべき等式の両辺にx^Lをかけ、Lを1から無限まで動かして和をとれば、左辺はf(x) - 1になる。右辺も変形すれば

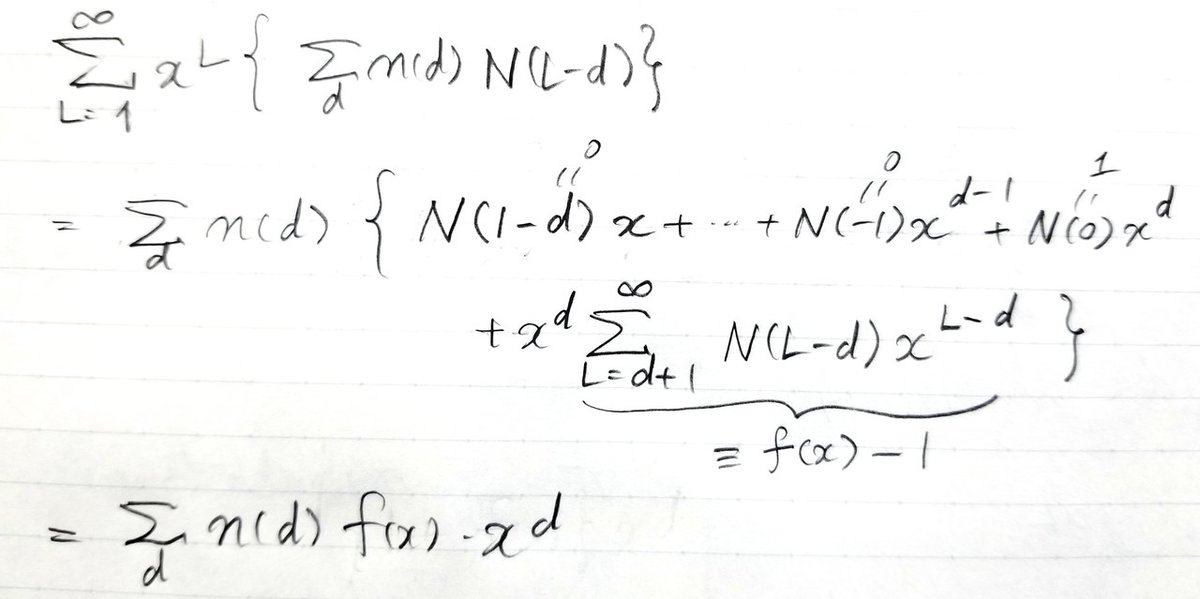
となるので、結局

が得られます。母関数の分母にある和で表された関数をgとします:

この滑らかな関数はg(0)=0であり、明らかにxについて単調増加です。さらにf(x)は0<=x<1/2の範囲で絶対収束します。なぜなら

だからです。よってf(x)はこの範囲で極をもたないはずです。するとg(x)はこの範囲で１に等しくなることはない。つまりこの範囲でg<1が言える。x→1/2とすれば

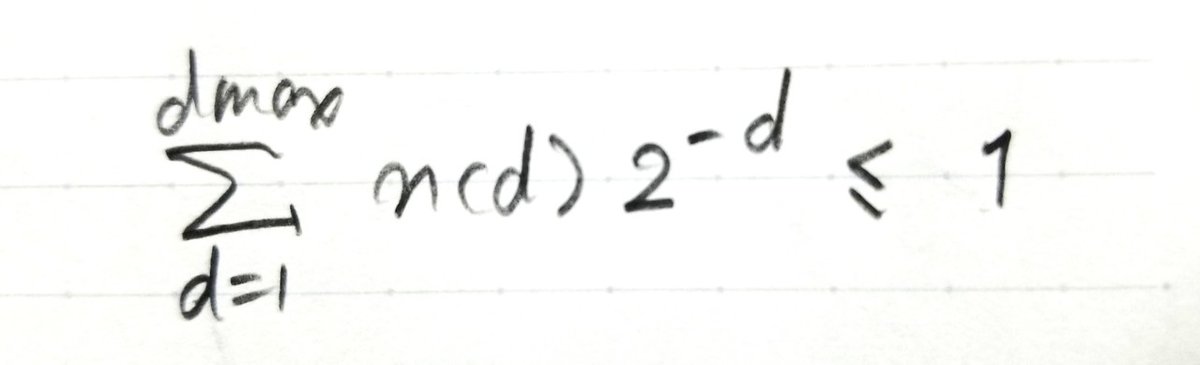
が言える。この左辺をよく見ると、和をkに直してみれば、示したかったKraft-McMillanの不等式の左辺に一致しています。

ちなみにこの逆も言えます。つまりK個の自然数の組{d1, …, dK}が与えられたとき、これらの自然数がKraft-McMillanの不等式を満たせば、復号可能な符号でこの符号長をもつ符号が存在することを示せるのです。この証明は機会があれば紹介します。詳細は文献[2, 4]にあります。

瞬時復号可能性へ

次回は復号可能な符号の中のさらに狭いクラスである、瞬時復号可能な符号を考察し、Kraft-McMillanの不等式が瞬時復号可能な(符号が存在する)ための必要十分条件であることを示します。これによって最適な符号の探索範囲を瞬時復号可能な符号に限って考えることができます。

というのも、もしある符号が復号可能であれば、それは上の議論によってKraft-McMillanの不等式を満たし、すると次回示す定理によって同じ{dk}の組で瞬時復号可能な符号が存在することが示せるからです。つまり{dk}をまったく変えないまま、瞬時復号可能な符号へと考察を移すことができる。この意味で次に考えるのは瞬時復号可能な符号の定義とその最適化になるわけです。

参考文献

[1] L.G.Kraft, "A Device for Quantizing, Grouping and Coding Amplitude-Modulated Pulses," M.S.Thesis, Dept. of Electrical Engineering, MIT, Cambridge (1949).

[2] B.McMillan, "Two Inequalities Implied by Unique Decipherability," IRE Transactions on Information Theory 2, 115 (1956).

[3] W.Feller, "An Introduction to Probability Theory and its Applications," 3rd ed. (Wiley, New York, 1968), Vol. 1.

[4] クロード・E.シャノン、ワレン・ウィーバー、『通信の数学的理論』、植松友彦訳、ちくま学芸文庫 (2009).

[5] R.G.Gallager, "Information Theory and Reliable Communication" (John Wiley & Sons, New York, 1968).