見出し画像

ARIMAモデルでnoteの週間アクティブユーザー数を予測する

hanaori

今年早々、note の月間アクティブユーザー数が1,000万人を突破したという記事が出たと思います。

実際 note はかなりの勢いで成長していますが、はたして過去のデータを用いて今後の成長の予測ができるのかどうか気になりました。

今回はGAの週間アクティブユーザー数データを用いて、どのようにnote が成長しているのか、次週のアクティブユーザー数が予測できるのかを見ていきたいと思います 😊

■ 原系列・差分系列・対数差分系列の確認

画像1

① 原系列

・ 各時点で期待値・ばらつきが異なる非定常なデータ
     → 差分を取ってプロットしてみる

※ 定常なデータ（ここでは弱定常のこと）：
１） 期待値が各時点で一定、２） 分散・共分散が各時点で一定

② 差分系列

・ 期待値が一定になっている
・ 後半、ばらつきが徐々に大きくなることから、週間アクティブユーザー数は指数的に増加していると考えられる
     → 対数を取って差分系列をプロットしてみる

③ 対数差分系列

・ 後半のばらつきが等しくなり、定常なデータになっている

■ 変化点の確認

> res_cpts <- cpt.var(log_diff_users, method = "PELT")
> param.est(res_cpts)    
> plot(res_cpts)    
> cpts(res_cpts) 
[1] 20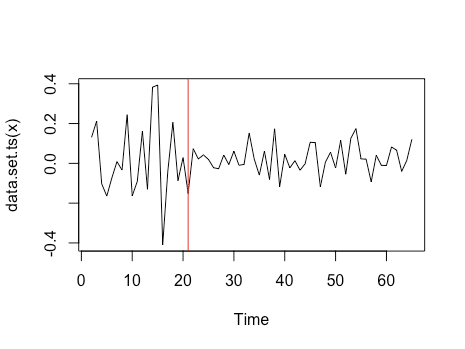

画像2

ARIMAモデルは非定常のデータに対しては使えないので、変化点（20週目）より後のデータを用いて推定していきます。

■ コレログラムの確認

対数差分系列のコレログラムを見てどういうモデルになりそうか確認したいと思います。

> acf(log_diff_users[21:65])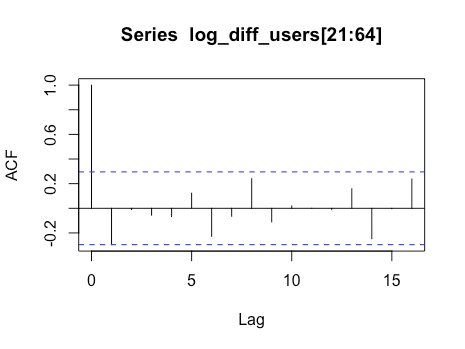

画像3

コレログラムを見るとlag 1まで自己相関がありそうだということが確認できます。
そのことから週間アクティブユーザー数の対数系列はARIMA(0, 1, 1)だろうと考えられます。

■ ARIMA(p,d,q)とは

コレログラムから、ARIMA(p = 0, d = 1, q = 1)ではないかと予測をたてました。
これがどういうモデルか見ていきましょう。

□ ARIMA(p,d,q)モデル

画像4

それぞれの要素がどういうものかもう少し詳しく見ていきたいと思います。

① AR(p)モデル：自己回帰モデル（AutoRegressive model）

画像5

モデル式からわかるようにARモデルは前時点までの結果から次の値を予測します。

画像6

左から AR(1)、AR(2)，AR(3) のコレログラムです。 ARモデルは前時点までの結果を用いて予測するため、ある時点での効果がその先までずっと受け継がれていきます。
その結果自己相関のコレログラム（ACF）ではARであることはわかりますが n がいくつになるか判別がつかないため、経由してる時点を除いた２点の直接の相関である偏自己相関コレログラム（Partial ACF）を見て判断します。

② lag(d)

画像7

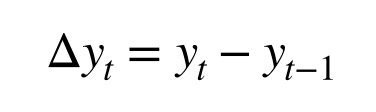
先ほどデータを定常にするため、差分をとりました。
前後の時点で１回差分をとったものを１階差分といいます。
そこからさらに差分をとったものは２階差分です。

画像8

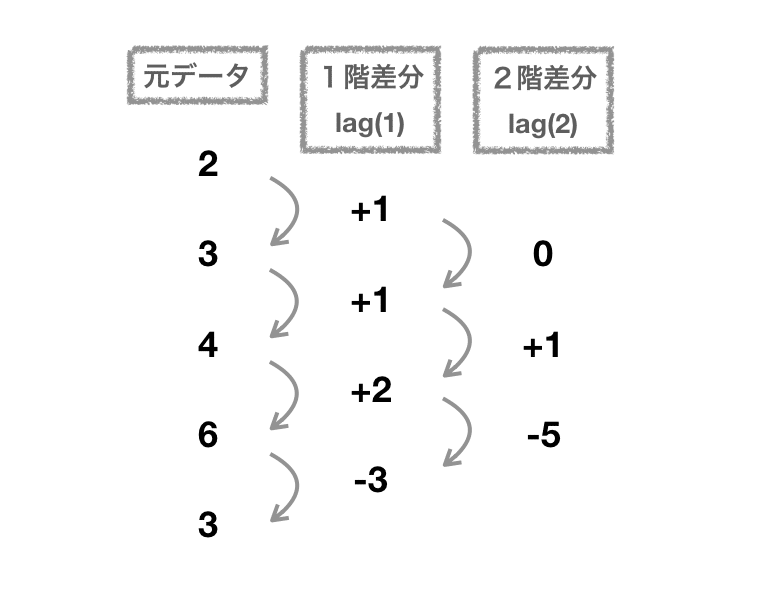
今回は１回しか差分を取らなかったので、d=1 になります。

③ MA(q)モデル：移動平均モデル（Moving Average model）

画像9

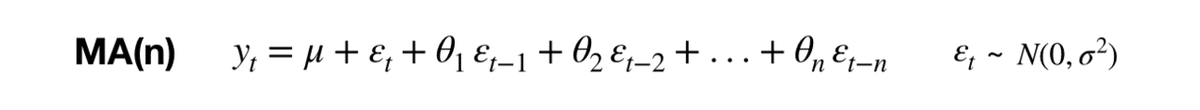
ε_tはホワイトノイズを表し、MA(3)だと過去３時点分のホワイトノイズを用いてy_tを予測します。

画像10

左から MA(1)、MA(2)，MA(3) のコレログラムです。 MAは自己相関コレログラムを見て、n がいくつになるかを判断します。

■ トレーニングデータとテストデータを作成

> n_users_term <- as.ts(log_users[21:65])
> train <- window(n_users_term, 1, 41)
> test <- window(n_users_term, 42, 46)

■ auto.arima()でモデルの確認

どういうARIMAモデルになりそうか、auto.arima()で確認しておきたいと思います。

> library(forecast)
> res <- auto.arima(train, ic = "aic",
                  stepwise = FALSE, approximation = FALSE,
                  max.p = 10, max.q = 10, max.order = 20, 
                  parallel = TRUE, num.cores = 4)

> res
Series: train 
ARIMA(0,1,1) with drift 

Coefficients:
          ma1   drift
      -0.3806  0.0213
s.e.   0.1718  0.0066

sigma^2 estimated as 0.004687:  log likelihood=51.47
AIC=-96.95   AICc=-96.28   BIC=-91.88

auto.arima()でもARIMA(0, 1, 1)になるという結果がでました。 
対数差分系列のプロットからはdriftを読みとることはできませんでしたが、プラスのdriftがありそうです。

※ ドリフト：前期との差の平均

■ 残差分析 

> tsdiag(res)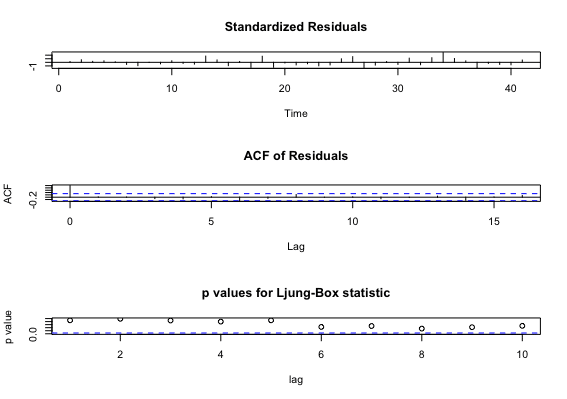

画像11

・ １つめの図から、等分散性がありそう
・ ２つめの図から、lag1以降の残差の自己相関が低い
・ ３つめの図から、自己相関が0でないlagも有意にはなさそう

以上から問題ないモデルと言えそうです。

※ 各図の意味
・ １つめ：残差プロット
・ ２つめ：残差の自己相関
・ ３つめ：lag nまでに自己相関が0でないlagがあるかの検定（縦軸はp値）
                   有意なら自己相関が0でないlagが存在するため、有意になっていないことを確認する

■ 予測精度を評価

# ARIMA(0,1,1)モデルを推定し、h時点後までを予測する
> pred_func <- function(x, h){
  res <- Arima(x, order = c(0,1,1), include.drift = T)
  return(forecast(res, h = h))
}

> error_all <- tsCV(n_users_term, pred_func, h = 1)
> error_test <- window(error_all, 41, 45)

> var(error_test)
[1] 0.004668056

# MAPE
> mean(abs(1 - exp(test + error_test) / exp(test)))
[1] 0.05556257

画像12

tsCV() はトレーニングデータでy_nを予測し、テストデータと比較して誤差算出するということを引数に渡したデータの各時点分行います。

今回、残差がとても低く、推定時の誤差分散とも大きく変わらないので精度はよさそうです。
MAPEから実際の値に対し、平均して5.56%予測がぶれそうなことがわかります。

■ ある時点の週間アクティブユーザー数着地予測

4/6までのデータを用いて、4/7~4/13のアクティブユーザー数を予測したいと思います。

> res <- Arima(log_users, order = c(0,1,1), include.drift = T)

> forecast(res, h = 1)
   Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
47       15.27245 15.18595 15.35895 15.14016 15.40474

対数から戻して、

・ 点推定推定量: 4292801
・ 80%信頼区間: 3937080~4680661

■ 結果

4/7~4/13のアクティブユーザー数

・ 予測：4,292,801
・ 現実：4,256,492

かなりいい線いってるのではないでしょうか ˆˆ

■ さいごに

以上から、noteの週間アクティブユーザー数の対数系列は ARIMA(0, 1, 1) モデルでかなり正確に予測することができました。
さらにそのことから、ありがたいことに note の週間アクティブユーザー数は指数的に増加していることがわかります。

たくさんの方に使ってもらえるのはとてもうれしいし、これからもこの成長を支えられるようにどんどんいい方向にカイゼンを積み重ねていきたいです。

P. S. こちらもおすすめ

Go AndoさんがData Analyst Meetupで発表した資料もnoteの成長背景が分かってかなり面白いです。
もしまだ見られてなければぜひ 😊✨

参考文献

・ 時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装
・ 年号の続いた年数の傾向を調べてみた。

いいなと思ったら応援しよう！

hanaori
( *ˆoˆ* )