
Rhinocerosで正弦曲線(サインカーブ)を描く方法
※こちらの記事は「お気持ち編」となります。実際に描く方法を提示しているのは『Rhinocerosで正弦曲線(サインカーブ)を描く方法・続』となりますので、そちらも併せてご覧ください。
正弦曲線(サインカーブ)とは
正弦曲線(サインカーブ)をご存知でしょうか。高校の数学で扱う三角関数を用いて描かれるグラフのことです。下の図には私が思う正弦曲線が描かれていますが、皆さんもこれと同様のものを想像するでしょう。規則正しい周期性を持ち、円周に次いで美しいこの曲線を、デザインや、またはふとした時に描かれる方は多いと想像します。

さて、この図に赤色で記されている、AとBという曲線上の点はお互いに近い位置にありますが、これらの近さは一体どれだけでしょうか。手描きでこの曲線を描くとき、「AとBは隣り合っていて、その間に他の点は存在しない」としても、皆さんは問題なくAとBを結んで正弦曲線を描き切ることはできるでしょうし、私の場合においてもそうです。しかし、そうして描かれたこの図において、AとBとの間には他の点を記せそうな箇所が曲線上に現れてしまっているのがわかります。正弦曲線と、それを描く前と描いた後に、認識する「正弦曲線」との違いはどれほどあり、どちらが正しいのでしょうか。
冒頭に示したように、正弦曲線は数学によって定義されています。そうでない正弦曲線もあるかもしれませんが、「正弦曲線」という言葉の、一般的に通用する意味では、これは直感的ではないため、ここでは考えないこととします。そして、数学という系は、全て論理によって作られています。物理学で発見された事実が数学に還元される場合もありますが、この場合でも、還元されたその事実は数学の文脈で構築されており、論理に紐付いています。すなわち、論理という、行動に先立って存在する構造で構築された、数学という系で考えられる正弦曲線は、それを描く前のものに一致します。このことをめぐる私の考えについては、以前書いた『私の建築』の「認識された建築」という項に同様のことが記されているのでご参考ください。
コンピュータ(計算機)上で扱えるRhinocerosは、やはり計算、そして数学によって図形を描画します。このRhinocerosでは、図中のAとBを座標によって間違いなく記すことができますが、この時点では、その間に記せそうな他の点を記すことは不可能です。これは、その点が図中に記されていないためです。この事実は、前述の正しい正弦曲線を描くのに適していて、つまり、ある数と、三角関数によってそれに対応する数の組み合わせを、{A,B,C,D,…}というようにそれぞれ決定していき、それらを座標によって描画し、その総体を正弦曲線とみなすことは可能です。
Rhinocerosで扱える図形
Rhinocerosで扱える図形はNURBS多様体というもので、そのうちの曲線として扱われているものは、一般に次の式で表現されています。
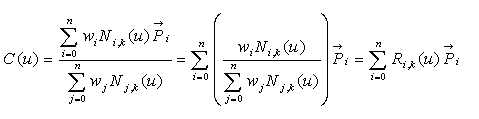
複雑な式ですが、ここでは最初の辺と最後の辺のみ見ます。これは、関数Cを用いて実数uから導かれた数ベクトル(点)C(u)と、関数Rを用いてuから導かれた実数R(u)と数ベクトルPの積の総和が一致するという方程式で、C(u)は点であって曲線ではないのです。
つまり、Rhinocerosで描かれている曲線は、点の集合であり、曲面の場合でもそうです。ここで当然の疑問として、前述のAやBのような点は、このNURBS曲線にどのように対応するかということが考えられます。
実数空間を使って曲線を描く
前項で「実数u」というものが登場しましたが、実数とはそもそもなんでしょうか。定規にメモリが振られているように、二つの異なる実数の間には大小関係などの関係性が存在しますが、例えば、0と1という実数は隣り合っているのでしょうか。0.1という実数は0と1の間に存在し、1よりも0に近いので、これは偽です。このことは代数学という分野で論じられており、詳しくは下記の『実数の構成に関するノート - 九州大学』のPDFをご覧ください。
さて、これで実数とは何か、その全貌を考えることができたわけですが、表題の「実数空間」なるものは何でしょうか。例えば、実数全体で見ると隣り合わない√2と√3との間にはどのような関係性があるのでしょうか。
定規という道具があります。小中学校での作図の授業で定規を持参することを要請された私は、義務教育課程を順当に経た、大多数の方は定規という道具を認知していると想像します。
多くの定規には、数字、または実数だと直感的に分かるものが目盛りに振られているかと思います。以下では、この定規について考えます。
こういった定規の目盛りと目盛りとの間の、目盛りが振られていないけれども、定規で線を引く時に通過する箇所にも実数が割り振られていることを想像できます。例えば、目盛り3と目盛り4の真ん中あたりの、目盛りが振られていない箇所は3.5だと想像できます。この箇所には、仮想的に目盛りが振られていると認識します。
また、ある長さの目盛りの分だけ定規で線を引き、この線の端点から、この線と平行かつ他方の端点に対して逆向きに、ある長さの目盛りの分だけ定規で線を引き、これら二本の線を一緒に定規で測ると、その二つの長さの合計値が導かれるでしょう。
こうした定規のうち、全ての実数の目盛りが振られた定規によって引かれる線を一次元のユークリッド空間と言えるでしょう。これの定義は以下を参照しています。
実数によって作られるこの空間のことを、ここでは実数空間と呼びます。先程の定規を使えば、実数空間のある点から√2と√3の長さの位置をそれぞれ、それらの近さと共に、導くことができます。
定規に限らず、実数で表現できるなんらかの長さを持つ線を引くとき、それは必ず実数空間の一部分となります。そうでない場合はありません。同様に、実数を扱うRhinocerosで描かれる線は実数空間の一部分であり、先程の疑問には以下のように答えることができます:
問 : 前述のAやBのような点は、このNURBS曲線にどのように対応するか。
答 : それらは実数空間に対応する実数である。
長くなってしまいましたが、それでは次の記事で実際にRhinocerosに正弦曲線を描きましょう。
この記事が気に入ったらサポートをしてみませんか?
