
SIGIR'20 Keynote speakerから見るInformation Retrievalの分析に関する誤り
SIGIR'20のkeynoteで,Norbert Fuhr氏がProof by Experimentation? Towards Better IR Researchというタイトルでプレゼンを行いました.訂正もなく多重検定を行っている論文は即座にリジェクトされるべきだと言ったメッセージもあり,その内容はかなりエッジが効いていました.それを簡潔にまとめると,
情報検索の分野では,実践的な有効性を確認するために,実験は重要な役割を果たしている.それにも関わらず,しばしば適用される評価手法は他分野の科学的水準に達していない.
Norbert氏によると,いくつかの原因が考えられると言っていました.Nobert氏の論文[1]をもとになぜIRの実験手法が良くないのか,そして,その対策についてより詳しい話を書いていこうと思います.
実験に関する問題点
Norbert氏が指摘した問題点はざっと上げると以下のよう.
評価指標の問題点
1. MRR,ERRのような評価指標は定義から不適切である.
2. MAPはユーザーの行動について非現実的な仮定をしている.
3. 算術平均の相対的な改善度合いは統計的に無意味である.
仮説検定に関する問題点
1. 仮説検定が実験の後に行われる.
2. 有意水準などの訂正なく,多重検定が行われている.
3. 効果量を無視している
実験に関する問題点
1. 多くの実験は再現性がない
それでは一つずつ詳しく見ていきます.
評価指標の問題点
① MRR,ERRのような評価指標は定義から不適切である
まずMRRの定義についてもう一度復習していきます.MRRとは,Mean Reciprocal Rank (MRR)の略で,Reciprocal Rank (RR)の平均を使った指標です.
それでは,RRの定義とはなんでしょうか?これは,検索結果の中で,relevantなdocumentの一番高い順位の逆数で定義されます.例えば,一番順位の高いrelevantなdocumentの順位をrとすると,RRは,以下のように定義されます.
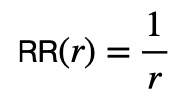
順位が小さければ小さいほど良いので,それの逆数であるRRは,大きければ大きいほど良いということになります.RRは,relevantなdocumentが上位に来れば良く,そのdocumentより下の検索結果については考慮していないです.これはユーザーが検索結果を上から下に見てrelevantな結果を発見したらそこで満足するという仮定に基づいています.この仮定を信じれば,RR自体は別に問題がなさそうです.
次にMRRについて具体的に計算する例を示します.ある検索システムAがあり,三つのクエリについて,それぞれ検索結果を返すとします.以下の図のように,最初のrelevantなdocumentが出てくる順位をそれぞれ1, 2, 4とします.

この時のそれぞれのRRを計算すると,RR(1) = 1, RR(2) = 1/2, RR(4) = 1/4となります.よって,システムAのMRRは,

のようになります.
実はMRRが奇妙な動きをします.比較対象を作るため新しいシステムBを考えます.システムBは先ほどの三つのクエリに対して,以下の図ようにrelevantなdocumentを2番目に表示するとします.

このシステムBのMRRを計算すると,
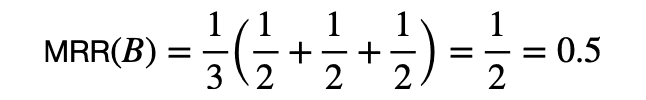
二つのシステムA, BをMRRで比較すると,
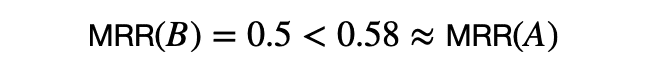
となり,システムAがシステムBより良いという結果になります.
しかし,もしRRのように逆数を取らず,順位自体の数値を直接指標として,小さければ小さいほどよいという単純な指標で平均をとった場合,どうなるでしょうか?この指標をMean First Relevant (MFR)とNorbert氏は呼んでいるので,踏襲します.
システムAのMFRを計算すると,
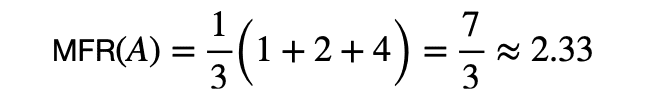
システムBのMFRを計算すると,
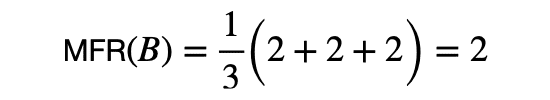
MFRは,relevantなdocumentが最初に来る順位をそのまま平均しているため,小さければ小さいほど良いです.したがって,システムBの方がシステムAより良いという真逆の結果になってしまいます.
これは期待値の基本的な性質で,逆数の期待値は期待値の逆数と必ずしも一致しないからです.
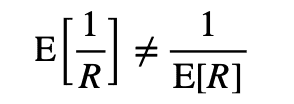
ただMRRの一番の問題は,平均するRRがinterval scale(間隔尺度)ではなく,ordinal scale(順序尺度)であることです.具体的には,以下の計算式でわかるように,順位が1と2である検索結果のRRの差と順位が2と∞である検索結果のRRの差が同じなのでinterval scaleでないことがわかります.

ordinal scaleでは平均に意味はないので,MRR自体,意味のない指標になっています.
一方で,先ほど計算したMFRは解釈次第ではinterval scaleになります.というのは,順位との差を,ユーザーが検索結果のdocumentを余分に多く読む労力と置き換えることができれば,順位の差に意味を持ち,interval scaleになりえます.例えば,relevantなdocumentの順位が2と3の検索結果は,ユーザーが余分に一つ多くのdocumentを見る必要があります.これは順位が4と5の検索結果でも労力の差は同じです.
また[2]で提案されたExpected Reciprocal Rank (ERR)についても同じ問題を抱えていることを指摘されています.ERRは,documentの関連度合いをユーザーがdocumentに満足する確率に変換して,満足する確率的な順位の逆数の期待値をとったものです.ERRについては,[2]やブログがわかりやすいです.
なぜERRが同じ問題を抱えているか考えてみるとすぐわかると思います.また逆数を用いなければ,この問題は解消されます.
今までの議論からMRR,ERRのような評価指標は定義から不適切であるということがわかりました.また順位をそのまま数値として扱えば解決できることもわかりました.
次にMean Average Precision (MAP)の問題点について話します.
②MAPはユーザーの行動について非現実的な仮定をしている
MAPの定義をする際に使うPrecision@kについて定義は以下の式で表されます.

つまり,Precision@kは検索結果のk番目までrelevantなdocumentsの割合を測っています.
これを用いて,MAPを定義します.定義は以下のようになります.

ただし,Rは全体のrelevantのdocumentsの数で,rel@kは検索結果のk番目のdocumentがrelevantかを表す指示関数です.
MAPはあるユーザーの行動モデルに基づいた指標になっており,そのユーザーの行動モデルの仮定は以下の二つです.
1. ユーザーはrelevantなdocumentを読んだあとのみ,検索結果を見るのをやめる(rel@kをかけている部分)
2. 検索結果を見るのをやめる確率は,relevantなdocumentがどの順位にいても一定である(1/Rで割っている部分)
MAPを仮定しているユーザー行動のモデルなどの詳しい説明は,[3]に譲ります.
Norbert氏は,2の仮定がナンセンスであると指摘しています.実際のユーザーの行動を見てみると,ほとんどのユーザーは検索結果の最初の方でみるのをやめて,最後の方まで見るユーザーは少数であると指摘した論文[4]を紹介しています.
MAPは全ての順位にいるrelevantなdocumentを均等に扱っているので,実際のユーザー行動を捉え切れていないと言っています.
より現実的な指標として,Rank-Biased Precision (RBP)[5]やdiscounted cumulative gain [6]を使うことを提案しています.
③ 算術平均の相対的な改善度合いは統計的に無意味である
提案手法と既存手法を比較するとき,相対的な改善をクエリ全体で算術平均をとって判断してしまうことがある.
例えば,システムAとBをある指標で比較した時,以下のようになったとします.

図のAverageは列ごとに平均をとったものです.図からわかるように相対的な改善の平均は(10 - 8) / 2 = 1%ですが,平均の相対的な改善は(0.35 - 0.36) / 0.35 = -2.85%です.
章題からもわかるとおり,相対的な改善の平均が間違いとなります.これは,確率変数と期待値の記号を使って考えるとわかりやすいです.システムAの評価をX,システムAに対するシステムBの相対的改善をKとすると(具体的には,上の図のQuery2に対してはX=0.5, K=0.08),
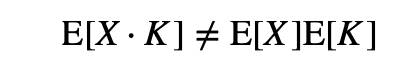
であるから,相対的な改善の平均であるE[K]は,以下のように計算できないのです.
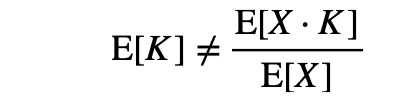
それゆえに,算術平均は絶対的な改善にのみ適用できるのです.
どうしても相対的な改善に対する平均を見たい場合は,幾何平均を使う必要があります.ただ幾何平均はratio scaleにしか使えないので注意が必要です.算術平均を使うか,幾何平均を使うかは評価したいシステムの差の性質によります.幾何平均の場合は,弱い結果にも強く影響し,算術平均は強い結果に強く影響します.
詳しくは,[7]のchapter 5に譲ります.
これで指標に関する問題点は終わりで,次に仮説検定に関する問題点に入ります.
仮説検定に関する問題点
① 仮説検定が実験後に行われる
仮説検定の基本的な知識のはずだがという前置きから始まります.
そもそも検定したい仮説が厳密に書かれていない.
実験を行う前に検定する仮説を記述しなければいけないが実験の結果がわかってから行われている.
各手法に対して,それぞれで検定をしなければいけないが,結果を見て有望な手法を決めてから,提案手法を有望な手法のみと比較するといったことが行われている.
② Correctionなく多重検定が行われている
いくつかのアプローチを考えてそれぞれで検定を行うことがあるが,有意水準を訂正しないまま行われている(多重検定問題).より具体的な対策は[8]に譲るとして,ここでは簡単な例を使って多重検定の問題点を復習します.
ある薬の効果を図るため薬を処方するグループとそうでないグループに分けて20の異なる症状に対して有意水準0.05の検定を行う.
この時,薬の効果が全くないとしても,少なくとも一つの検定で有意になる確率は50%を超える.なぜならば薬に効果がない元で,全ての仮説が有意にならない確率は,0.95^20なので,少なくとも一つが有意になる確率は,
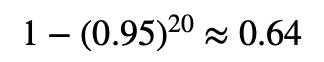
で思った以上に高い確率になります.
IRの文脈で話すならば,同じデータセットで,いくつかの指標を見る場合に上のようなことが起こります.
この時,適切に有意水準を訂正する必要がある.いくつかの訂正方法があるが,簡単な方法としてBonferroni Correctionと呼ばれる方法を挙げている.これは検定の数で下の有意水準を割ると言った訂正方法である.上の例では,20の検定を行うので,0.05/20 = 0.0025の有意水準を使って各検定を行う.そうすると,薬に効果がない条件で,少なくとも一つが有意になる確率は,0.048となります.
他にも[9]でも議論されているように,データの再利用は非常に結果をランダム化させてしまう問題があります.そのため,最低でも今までpublishされた実験のテストの数だけ訂正を行う必要があると指摘しています.
③ 効果量を無視している
仮説検定でわかることは,二つのアルゴリズムが同一の性能ではない可能性が高いということだけで,実際どれほど性能差があるのかは何も教えてくれない.ウェブなどで大量のデータが手に入る昨今では,どんなに小さな差であっても有意にできてしまいます.
precisionやrecallであれば,平均の差を解釈することは可能です.例えば,Precision@10の差が0.02であれば,5つのクエリの内1つ多くrelevantなdocumentが入っていることがわかります.しかし,RBPやNDCGと言った指標では効果の差を解釈するのが難しいです.
また効果量は単純な差だけでなく,分散も考慮したものもあります.
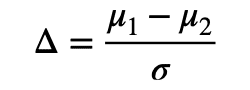
サンプルして得られた結果が帰無仮説からどれほど離れているかを定量化したものと解釈されます.ただし,σは標準偏差.
最後に実験に関する問題点を解説します.
実験に関する問題点
① 多くの実験は再現性がない
ACMは再現性に関して
A scientific result is not fully established until it has been independently reproduced.
と言っているが,実際には再現性が不可能な論文がたくさんあると主張しています.
その上で,Nobert氏は,使い古されているテストデータではなく,新しいテストデータの必要性も訴えています.
実装に関しては誰でも再現可能なようにその詳細を明確に記述すべきです.データに関していえば,公開できない企業内データなどでは公開ができないが,できる限りそのデータセットの特徴を記述し,データセットのあらゆる統計量を公開すべきであると言っています.
終わりに
Nobert氏が指摘した問題は難解な概念は何一つなく,基礎的な統計学の知識で間違いであることがわかるものばかりで反省しました.これは研究だけの話でなく,プロダクトで機械学習やIRのアルゴリズムを導入する際に同じく気をつけなければならない話です.
現実問題として実践が難しいものも多い(新しいデータセットを取得する)が,できる限り,実験の設計を見直し,指標や評価方法が性能を統計的に正しく,測ることができるのかということを再確認しなければいけないと思い知らされました.
またもし間違いなどあれば,ぜひコメントでご指摘いただければ幸いです.
リファレンス
[1] Fuhr, Norbert. "Some common mistakes in IR evaluation, and how they can be avoided." ACM SIGIR Forum. Vol. 51. No. 3. New York, NY, USA: ACM, 2018.
[2] Chapelle, Olivier, et al. "Expected reciprocal rank for graded relevance." Proceedings of the 18th ACM conference on Information and knowledge management. 2009.
[3] Robertson, Stephen. "A new interpretation of average precision." Proceedings of the 31st annual international ACM SIGIR conference on Research and development in information retrieval. 2008.
[4] Islamaj Dogan, Rezarta, et al. "Understanding PubMed® user search behavior through log analysis." Database 2009 (2009).
[5] Moffat, Alistair, and Justin Zobel. "Rank-biased precision for measurement of retrieval effectiveness." ACM Transactions on Information Systems (TOIS) 27.1 (2008): 1-27.
[6] Järvelin, Kalervo, and Jaana Kekäläinen. "Cumulated gain-based evaluation of IR techniques." ACM Transactions on Information Systems (TOIS) 20.4 (2002): 422-446.
[7] Thompson, Bruce. Foundations of behavioral statistics: An insight-based approach. Guilford Press, 2006.
[8] Carterette, Benjamin A. "Multiple testing in statistical analysis of systems-based information retrieval experiments." ACM Transactions on Information Systems (TOIS) 30.1 (2012): 1-34.
[9] Carterette, Ben. "The best published result is random: Sequential testing and its effect on reported effectiveness." Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2015.
この記事が気に入ったらサポートをしてみませんか?
