小学算数の復習（四則演算）

小学算数を学び始めた背景

第一子出産のために産休に入り、時間がたっぷりあったので今後のためにも小学算数を復習しようと思ったことから。
学びなおしをしてみると、「そうすることは知ってたけどなぜそうするのかは知らなかった」ということがけっこうあった気がする。
せっかく学びなおしをしているので記録に残して今後に役立てようと思う。

※今回記載している内容は自分が「なるほど！」と思ったもののみ記載している。一通り小学算数を復習したい方には以下の本を読んでもらうことをお勧めする。

参考にした本

小学算数の解きかたが1冊でしっかりわかる本　小杉 拓也 (著)

足し算と引き算

繰り上がりのある足し算／繰り下がりのある引き算はさくらんぼ計算で考える。（ちなみにさくらんぼ計算は2010年前後から算数の授業で取り入れられるようになっているようですね。）

さくらんぼ計算（足し算）

出典：https://xn--fdk3a7ctb5192box5b.com/es/1nen_mt_sakuranbo_tashi001.html

さくらんぼ計算（引き算）

出典：https://xn--fdk3a7ctb5192box5b.com/es/1nen_mt_sakuranbo_tashi001.html

かけ算

分配の法則

分配の法則を使えば２桁×１桁の掛け算は暗算できるようになる。
まず計算しやすい数に分解して後から足すのがポイント

1⃣　１０３×８
　＝（１００＋３）×８　　　　　# 103を100と3に分解して計算
　＝（１００×８）＋（３×８）   # 100と3にそれぞれ8をかける
　＝８００＋２４　　　　　　　 # 最後に足す
　＝８２４

2⃣　９６×７
　＝（１００－４）×７          # 96を100と4にして計算
　＝（１００×７）－（４×７）   # 100と4にそれぞれ7をかける  
　＝７００－２８　　　　　　　 # 4足した分を最後に引く
　＝６７２

3⃣　４３×６
　＝（４０＋３）×６
　＝（４０×６）＋（３×６）
　＝２４０＋１８
　＝２５８

おみやげ算

おみやげ算も↑と同様に計算しやすい数に変形してから計算するのがポイント

１４×１３の場合
（１７×１０）＋（４×３）に式を変形

出典：https://onigiriface.com/omiyagezan-sukai.html

　１７×１２
＝｛（１７＋２）×（１２－２）｝　# 1⃣ 17に2を足して19に、12から2を引いて10にする
　　　＋（７×２）　　　　　　　　# 2⃣ ↑に1の位の7と2をかけたものを足す
＝（１９×１０）＋１４
＝１９０＋１４
＝２０４

でもなぜこの計算が成り立つの・・？

おみやげ算の証明

17×12＝は縦×横の掛け算。図で表すと以下の四角形になる。

出典：https://onigiriface.com/omiyagezan-syomei.html

”17に2を足して19に、12から2を引いて10にする”を図にすると以下のようになる。（キリのいい数字に変形）

出典：https://onigiriface.com/omiyagezan-syomei.html

変形してできた式 ”１９×１０”は四角形の白い部分、
一の位７×２ははみ出ている赤い四角形部分なので
この二つの四角形を足すと答えが出る。

出典：https://onigiriface.com/omiyagezan-syomei.html

割り算

これは小学算数の範囲かどうか微妙ですが、興味深かったので載せておきます。

割られる数が０の時

０÷３＝０

答えは当然０
０個のお菓子を３人で分けても０個ですよね。

割る数が０の時

３÷０＝解なし

割る数が０の時は解なしとなります。
３個のお菓子を０人で分ける・・？
この問いに答えることはできないので解なし。

より詳しく

それじゃ納得できない！という私のために深堀。

Ａ÷Ｂという割り算の答えが知りたければ，Ｂ×（　）＝Ａという式を作り，（　）の中に何が入るか考えればよいことになりますね。
０÷３の答えは　３×（　）＝０という式を考えれば，
０だとすぐ分かります。

では，問題の「３÷０」の場合はどうなるでしょうか。
この答えは，「０×（　）＝３」という式を考えれば分かるはずなのですが・・そんな数などない！

ということで３÷０は解なしとなります！

出典：https://naop.jp/2021/06/04/0dewaru/

計算の順序

計算の順序の基本は
①ふつうは左から計算
②×と÷は＋と－より先に計算
③かっこのある式はかっこ内を一番先に計算

　６＋（１０－９÷３）×（２＋３）
＝６＋（１０－３）×（２＋３）　　　# 9÷3が１番　　　　　　（カッコ内の÷）
＝６＋７×５　　　　　　　　　　　　# 10-3が2番、2+3が3番　（カッコ内の＋と－）
＝６＋３５　　　　　　　　　　　　 # 7×5が4番　　　　　　 （カッコ外の×）
＝４１　　　　　　　　　　　　　　 # 6+35が最後　　　　 　（カッコ外の＋）

ネットニュースを見ていると最近この計算の順序がわかってない人が多いらしいですね。「私は知ってたぞ！」という人もなぜ「×と÷は＋と－より先に計算するか」ということを説明できない人が多いのではないでしょうか。

なぜ×と➗は＋と−より先に計算する？　カギは「単位」にあり

「たし算」や「ひき算」は、同じ単位のもの同士しか、足したり引いたりできない。

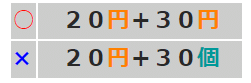
例えば、「２０円」と「３０円」を足して、「５０円」にすることはできる。
しかし、「２０円」と「３０個」を足して「５０」にすることはできない。
単位が揃っていないと使えないのが、「たし算」や「ひき算」である。

出典：http://www6.plala.or.jp/maeda-masahide/9kakewarisaki.html

それに対して、「かけ算」や「わり算」は違う単位のもの同士でも、掛けたり割ったりできる。
例えば「２０円」の物が「３０個」あるなら、２０に３０を掛けて、「６００円」になる。
単位が揃っていなくても使えるのが、「かけ算」や「わり算」なのである。

出典：http://www6.plala.or.jp/maeda-masahide/9kakewarisaki.html

こうした特徴を考えると、先に「かけ算」や「わり算」をしないといけない理由が分かる。先に「かけ算」や「わり算」して単位を揃えてやらないと、「たし算」や「ひき算」は使えないのである。

例えば、１２０円のチョコを１個と、２０円のガム３０個を買った場合を考えてみたい。
「円」と「個」がまざった場合である。

こんな場合、先に「２０円×３０個＝６００円」と「かけ算」をしなければならない。
かけ算をすることで、単位が「円」に揃う。
単位が揃ってはじめて「１２０円＋６００円＝７２０円」と、たし算が使えるのである。

※説明はhttp://www6.plala.or.jp/maeda-masahide/9kakewarisaki.htmlより丸パクリさせていただいてます。すみません、わかりやすかったもので。

感想

いままで「計算はできるけど、なぜそうするのか」までわからなかったことが多かったので、深堀して調べていくと新たな発見が多く面白かった。
次回（書く気力があれば）は小数や分数に触れていければいいなと思っている。