統計検定準一級受験記録② 1章～3章

今回の記事から、統計検定準一級受験時に重要だと思った点を、統計学実践ワークブックをもとに僕なりにまとめていきます。専門的、厳密な解説はできませんが、誤りなどのご指摘があれば加筆修正を行っていきます。

1. 事象と確率

1-1 事象と確率

■包除原理
$${P(A \cap B) = P(A) + P(B) - P(A \cup B)}$$
基本の式。$${P(A)}$$と$${P(B)}$$を足すと$${P(A\cap B)}$$の部分がダブるので、それを引くとちょうど$${P(A\cup B)}$$になる。
下記のベン図で理解すると良い。

包除原理

1-2 条件付き確率とベイズの定理

■条件付き確率
$${P(B \vert A) = \cfrac{P(A \vert B)}{P(A)}}$$ $${\iff}$$ $${P(B \vert A)×{P(A)}= P(A \cap B)}$$
ベン図で$${P(A \cap B)}$$と$${P(B \vert A)}$$の違いを表現すると下図のようになる。$${P(A \cap B)}$$は外枠の四角形に対する色塗り部分の面積の割合。$${P(B \vert A)}$$は事象$${A}$$に限った中での色塗りの割合。面積の割合と考えることで$${P(A \cap B)}$$を$${P(A)}$$で割る操作の意味が分かりやすくなると思う。

条件付き確率

■ベイズの定理
$${P(A \vert B) = \cfrac{P(B \vert A)P(A)}{P(B)} = \cfrac{P(B \vert A)P(A)}{P(B \vert A)P(A)+P(B \vert A^{C})P(A^{C}) }}$$

$${P(A \cap B)}$$は$${P(B \vert A)×{P(A)}}$$とも表現できるし$${P(A \vert B)×{P(B)}}$$とも表現できる。これらをイコールで結び式変形したもの。
$${P(A \vert B)}$$を事後分布、右辺分子の$${P(A)}$$を事前分布と言う。
ベイズの定理はいろんなところで使う。

分母の式変形は以下の考え方による。
$${P(B)=P(B\cap A)+P(B\cap A^C)=P(B \vert A)P(A)+P(B \vert A^{C})P(A^{C}) }$$

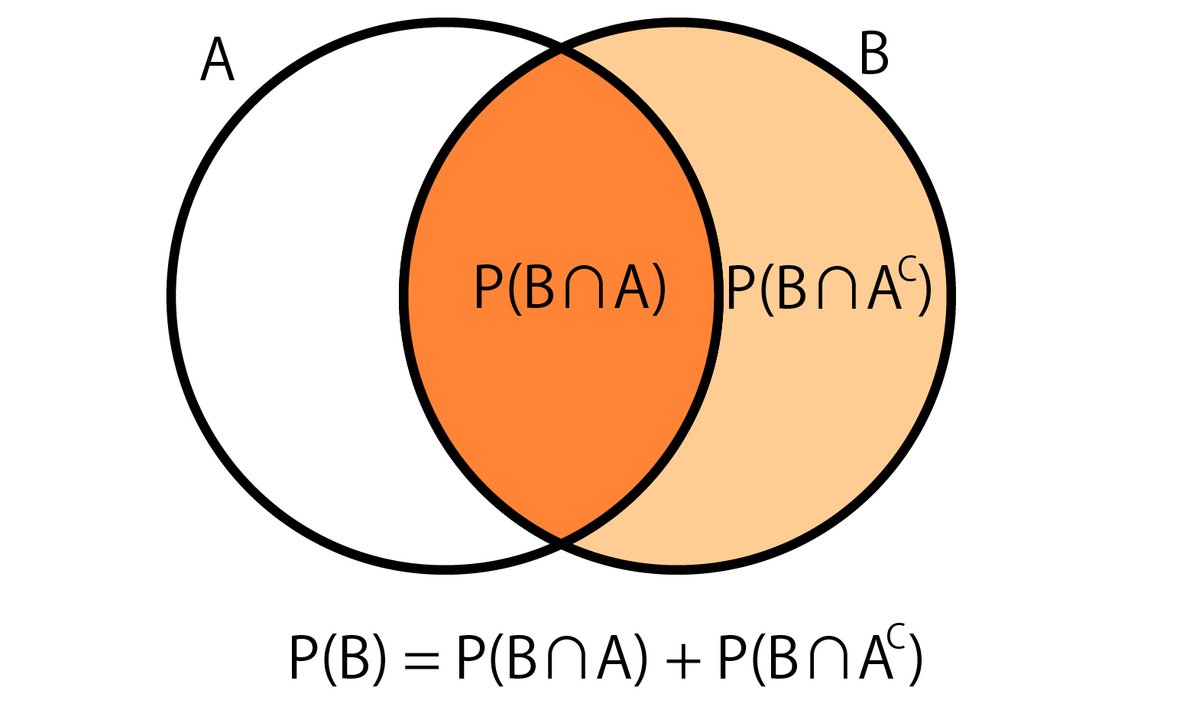
また、以下のように全事象$${\Omega}$$が事象$${A_i}$$の和かつ、$${A_i,A_j}$$が排反の時、（ワークブックP.3 図 1.2のような時）
$${\Omega = A_1\cup A_2\cup \cdots \cup A_k}$$かつ$${A_i \cap A_j = \emptyset}$$ $${(i\neq j)}$$
と表現できて、

$$
\begin{align*}
P(B)&=P(B\cap A_1)+\cdots +P(B\cap A_k)　　　　　　　　　　　　　　　\\
&=P(B \vert A_1)P(A_1)+\cdots +P(B \vert A_k)P(A_k)\\
\end{align*}
$$

と書ける。
よって

$$
\begin{align*}
P(A_i\vert B)&=\cfrac{P(B\vert A_i)P(A_i)}{P(B)}　　　　　　                  \\
&=\cfrac{P(B\vert A_i)P(A_i)}{{\textstyle\sum_{j=1}^k}P(B\vert A_j)P(A_j)}
\end{align*}
$$

これは、統計2級の本では故障（事象$${B}$$）とその原因（事象$${A_i}$$）の関係として説明されている。

■独立
事象AとBが独立であるとは
$${P(A \cap B)=P(A)×P(B)}$$
図にすると以下のような感じ。
$${B}$$という条件を置いても、$${B^C}$$という条件を置いても、あるいは何も条件を置かなくても、$${P(A)}$$の面積の割合に影響はない。
28章分割表で出てくる一様性の仮説はまさにこれ。

独立

■条件付き独立
$${P(A\cap B\vert C)=P(A\vert C)P(B\vert C)}$$
図で表すと下のような感じだろうか。具体的にどういう場合にこうなるのかはわからないけど。

条件付き独立

1-3 期待値と分散

$${\mu=E[X]=\displaystyle\sum_{x}xp(x)}$$
$${\sigma ^2=V[X]=E[(X-\mu)^2]=\displaystyle\sum_{x}(x-\mu)^2p(x)}$$

$${E[X]=\displaystyle\int^\infty_{-\infty}xf(x)dx}$$

$${V[X]=\displaystyle\int^\infty_{-\infty}(x-\mu)^2f(x)dx}$$

また、重要な関係式として

$${V[X] = E[X^2]-(E[X])^2 = E[X^2] - \mu^2}$$

分散の正の平方根をとったものが標準偏差。

$${\sigma=\sqrt{V[X]}}$$

ここで語られているのは分布の形（母集団）が明らかになっている場合の話。
後々、標本の分散だとか統計量の分散だとかが出てくるのでややこしい。ここで言っているのは分布の分散と期待値。

2. 確率分布と母関数

2-1 累積分布関数と生存関数

生存関数
確率変数$${X}$$が寿命を表す時、$${S(x)=1-F(x)}$$は時刻$${x}$$で生きている確率を表す。ただし$${F(x)}$$は$${f(x)}$$の累積分布関数。$${S(x)=1-F(x)}$$は生存関数と言う。

なんで$${S(x)=1-F(x)}$$が時刻$${x}$$で生きている確率なのかというと、

$${f(x)}$$は時刻$${x}$$で死亡する確率。
→$${F(x)}$$は時刻$${x}$$までに死亡する確率。
→$${S(x)=1-F(x)}$$は時刻$${x}$$までに死亡しない確率、すなわち生きている確率。

と考える。ある環境にネズミを放して、死ぬまでの時間を計測するのを何回も観測する（$${f(x)}$$の分布に従った結果が得られる）みたいなのを考えるとイメージがつきやすいのでは。

ハザード関数
$${h(x)=\cfrac{f(x)}{1-F(x)}=(-\log S(x))'}$$

■$${f(x)}$$と$${h(x)}$$の違い。
上記の例で、ある環境に1000匹のネズミを放したとして、ある時刻での死亡確率は分かっているとする。そして、1時間経過時点で死亡する確率は3%、確率通りにいくと1時間後にはネズミが100匹まで減っているとする。
最初に放った1000匹のうち30匹ぐらいが1時間時点で死亡すると思われる。これが$${f(x)}$$。
1時間経過時点で残っているネズミは100匹であり、そのうち30匹が死ぬということは、その時点で残っているネズミの30％が近々死ぬということになる。これが$${h(x)}$$。

最右辺への変形は、
$${\cfrac{f(x)}{1-F(x)}=\cfrac{-(S(x))'}{S(x)}}$$
と考えると出てくる。

2-2 同時確率密度関数

■同時確率関数
2変数の離散確率分布で$${X=x}$$と$${Y=y}$$が同時に起きる確率
$${P(X=x,Y=y)=p(x,y)}$$
連続分布の場合は、$${X,Y}$$がある範囲（$${x_1 < X  \leq x_2, 　y_1 < Y \leq y_2}$$）に同時に入る確率を考える。
$${P(x_1 < X  \leq x_2, 　y_1 < Y \leq y_2) = \displaystyle\int^{x_2}_{x_1}\displaystyle\int^{y_2}_{y_1}f(x,y)dxdy}$$

■周辺確率関数
$${X}$$の周辺分布→全$${y}$$についての確率を足し合わせる。
$${p_{X}(x) = \displaystyle\sum_{y}p(x,y)}$$
これは
$${P(B_i) = P(B_i \cap A_1)+\cdots +P(B_i \cap A_n)}$$
のようなイメージで考えるといいと思う。

（さいころを2個投げて、2回目に2が出る確率は「1回目に1が出て2回目に2が出る確率」+「1回目に2が出て2回目に2が出る確率」+・・・+「1回目に6が出て2回目に2が出る確率」のような）

連続分布の場合はシグマを積分に置き換える。
$${f_{X}(x)=\displaystyle\int^\infty_{-\infty}f(x,y)dy}$$

■条件付き確率関数
1章の時のように、$${X=x}$$がすでに起きているエリアを分母と考えることになる。分子に来るのは同時確率関数。
$${X=x}$$となる確率は$${p_{X}(x)}$$なので、
$${p_{Y\mid X}(y\mid x)=\cfrac{p(x,y)}{p_{X}(x)}}$$
連続の場合は
$${f_{Y\mid X}(y\mid x)=\cfrac{f(x,y)}{f_{X}(x)}}$$

2-3 母関数

①確率母関数$${G(s)}$$
$${X}$$が整数値の時に主に用いられる。
$${G(s)=E[s^X]=\displaystyle\sum_{x}s^xp(x)}$$
$${G'(s)=E[Xs^{X-1}],     G''(s)=E[X(X-1)s^{X-2}}$$
なので
$${G'(1)=E[X],     G''(1)=E[X(X-1)]}$$
よって
$${E[X] = G'(1),     V[X] = G''(1)+G'(1)-(G''(2))^2}$$
この計算は自分でできた方が良いと思う。

②モーメント母関数$${m(\theta)}$$
$${X}$$が連続（実数）の時に主に用いられる。
確率母関数の$${s}$$を$${e^\theta}$$としたもの。
$${m(\theta)=E[e^{\theta X}]}$$
$${m'(\theta)=E[Xe^{\theta X}],    m''(\theta)=E[X^2 e^{\theta X}]}$$
なので
$${m'(0)=E[X],    m''(0)=E[X^2],  \cdots  m^{(k)}(0)=E[X^k]}$$
よって
$${E[X] = m'(0),     V[X] = m''(0)-(m'(0))^2}$$

■母関数の性質
①各種確率分布と母関数の形とが、1対1で対応している。
　母関数の形が同じならその確率変数が従う確率分布も同じ。
　後の章の再生性の話とかで使われる。
②独立な変数の和に対して母関数を取ると、
　各変数の母関数の積の形になっている。
　すなわち
　$${X_1, X_2}$$のモーメント母関数をそれぞれ$${m_1(\theta), m_2(\theta)}$$とすると
　$${X_1+X_2}$$のモーメント母関数は$${m_1(\theta)m_2(\theta)}$$
確率変数3つ以上の和でも同じく3つ以上の積になる。

3. 分布の特性値

3-3 確率変数の分布の特性値

ここで語られているのは、1章の時と同じく分布の形が明らかな場合の話。

■期待値
平均値。計算上、ある$${X=x}$$の値とそれが起こる確率の積の和（連続分布だと値と確率密度も積の積分）なので、右の方に裾が伸びているとその影響を受けて期待値も大きくなっていく。

■中央値
$${P(x\leq a)=0.5}$$となる$${a}$$（連続分布）
$${P(x\leq a)\geq 0.5}$$ かつ $${P(x\geq a)\geq 0.5}$$となる$${a}$$（離散の場合、下図参照）

上式の0.5のところを0.75にすると第3四分位数（75パーセンタイル点）。0.25にすると第1四分位数（25パーセンタイル点）。第3四分位数と第1四分位数の差が四分位範囲（IQR）。

■最頻値
$${f(x)}$$が最大となる$${x}$$（連続）
$${p(x)}$$が最大となる$${x}$$（離散）

右に裾が長い分布の場合、最頻値 < 中央値 < 期待値となる傾向がある。
左に裾が長い場合は逆。

■標準偏差
$${\sqrt{V[X]}}$$
分散の正の平方根

■変動係数
$${\sqrt{V[X]}/E[X]}$$
標準偏差÷期待値。

■歪度
$${\cfrac{E[(X-E[X])^3]}{(V[X])^{3/2}}}$$
左右対称の場合0。
分布の裾が右に長ければ正、左に長ければ負となる傾向がある。

■尖度
$${\cfrac{E[(X-E[X])^4]}{(V[X])^{2}}}$$
上式だと正規分布の尖度は3。
正規分布を0と定義するために、上式から3を引いたものを尖度の定義とする場合もある。

3-2 同時分布の特性値

■相関
二つの確率変数$${X,Y}$$について以下の関係が言える。

・正の相関
$${X}$$が平均より大きい値を取る時は$${Y}$$も平均より大きい値を取りやすく、
$${X}$$が平均より小さい値を取る時は$${Y}$$も平均より小さい値を取りやすい。

・負の相関
$${X}$$が平均より大きい値を取る時、$${Y}$$は平均より小さい値を取りやすく、
$${X}$$が平均より小さい値を取る時、$${Y}$$は平均より大きい値を取りやすい。

相関には強弱があり、相関がない（独立）場合もある。

■共分散
$${Cov[X,Y]=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]}$$

$${X}$$と$${Y}$$が独立の時は共分散0になる。

■相関係数
$${\rho[X,Y]=E[(\cfrac{X-E[X]}{\sqrt{V[X]}})(\cfrac{Y-E[Y]}{\sqrt{V[Y]}})]=\cfrac{Cov[X,Y]}{\sqrt{V[X]V[Y]}}}$$
$${X}$$と$${Y}$$が独立の時は相関係数0になる。

■条件付き期待値、条件付き分散
$${E[Y\vert X]=\displaystyle\int^{\infty}_{-\infty}yf_{Y\vert X}(y)dy=\displaystyle\int^{\infty}_{-\infty}y\cfrac{f(x,y)}{f_{X}(x)}dy}$$
$${V[Y\vert X]=E[Y^2\vert X]-(E[Y\vert X])^2}$$
これらは$${x}$$の関数になっている。

この辺りの特性値同士の関係式は使う場面が多い。

3-3 特性値の性質

以下、$${X, Y}$$は確率変数、$${a, b, c}$$は定数。

■期待値の関係式。
$${E[aX+bY+c]=aE[X]+bE[Y]+c}$$
ここまで出てきてないけど$${E[c]=c}$$
$${X}$$と$${Y}$$が独立であれば
$${E[XY]=E[X]E[Y]}$$
ちなみに独立でなければ$${E[XY]=E[X]E[Y]+Cov[X,Y]}$$

■分散の関係式。
$${V[aX+b]=a^2V[X]}$$
$${X}$$と$${Y}$$が独立であれば
$${V[X\pm Y]=V[X]+V[Y]}$$
独立でなければ
$${V[X\pm Y]=V[X]+V[Y]\pm 2Cov[X,Y]}$$

式の導出にも問題を解くにも、ここらへんの式がよく出てくる印象。

■条件付き期待値、分散の関係式
$${E[E[X\vert Y]]=E[X]}$$
↑複合ポアソン過程の期待値計算で使われている。
$${V[X]=E[V[X\vert Y]]+V[E[X\vert Y]]}$$

★データの特性値

以降は得られたデータ（標本）に対する特性値。
データは$${x_1, \cdots x_n}$$とする。
■平均（算術平均）
$${\bar{x}=\cfrac{1}{n}\displaystyle\sum^n_{i=1}x_i}$$

■不偏分散
$${s_x^2=\cfrac{1}{n-1}\displaystyle\sum^n_{i=1}(x_i-\bar{x})^2}$$
$${n-1}$$ではなく$${n}$$で割ったものは標本分散。
8章で出てくるが、標本分散は正規分布の分散の最尤推定量になる。

■加重平均
$${w_1x_1+\cdots +w_nx_n}$$
ただし、$${w_1+\cdots +w_n=1}$$
値段$${x_i}$$円の商品が$${y_i}$$個ずつ売れた時の平均売上（1品あたりの平均売上単価）のように重み$${w_i}$$をかけて計算される量。
この例では$${w_i=y_i/(y_1+\dots +y_n)}$$が、全商品の売数の中で商品$${i}$$が売れた個数の割合を表している。

■幾何平均
$${(x_1×\cdots ×x_n)^{1/n}}$$
月ごとの成長率の平均のように、掛け算で累積されるものの平均を求める時に使う。

■調和平均
$${\cfrac{1}{\cfrac{1}{n}\displaystyle\sum^{n}_{i=1}(1/x_i)}}$$
データの逆数の算術平均（上の式の分母）の逆数。
速度のような、「〇〇あたりの△△（割合）を表す量」の平均を求める時に使う。

3-4 平均ベクトルと分散共分散行列

$${\bold X=(X_1,\cdots , X_k)^\top}$$を$${k}$$次元確率ベクトル（$${k}$$個の確率変数を要素とするベクトル）とすると、分布の期待値ベクトルは
$${\bold \mu=(\mu_1, \cdots,\mu_k)^\top}$$
分散共分散行列は
$${\Sigma=\begin{pmatrix}\sigma_{11}&\sigma_{12}&\cdots &\sigma_{1k}\\\sigma_{21}&\sigma_{22}&\cdots &\sigma_{2k}\\\vdots&\vdots&\ddots &\vdots\\\sigma_{k1}&\sigma_{k2}&\cdots &\sigma_{kk}\end{pmatrix}}$$
$${\bold X}$$の$${i}$$番目と$${j}$$番目の確率変数の分散$${(i=j)}$$、共分散$${(i\neq j)}$$を行列の$${i,j}$$成分に並べたもの。

また、標本を$${\lbrace \bold x_1,\cdots ,\bold x_n \rbrace}$$（$${\bold x_i}$$は$${k}$$次元のベクトル）とすると、標本の平均ベクトルは
$${\bold{\bar x}=\cfrac{1}{n}\displaystyle\sum^n_{i=1}\bold x_i}$$
分散共分散行列は
$${S=\cfrac{1}{n-1}\displaystyle\sum^n_{i=1}(\bold x_i-\bold{\bar x})(\bold x_i-\bold{\bar x})^\top}$$
$${S}$$の計算は、$${(\bold x_i-\bold{\bar x})}$$を$${\begin{pmatrix} x_{i1}-\bar x_1\\x_{i2}-\bar x_2\\\vdots\\x_{ik}-\bar x_k\end{pmatrix}}$$と成分表示で書いて計算すると確かに分散共分散の形になっていることが分かる。

今後、特に多変量解析の章などで行間を埋めながら読むためには行列に慣れておいた方がよい。また、問題を解くためにも必要な場合がある。例えばマルコフ過程の章で定常分布を求める問題など。